Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve Block Issue - Improvement Required
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve Block Issue - Improvement Required
I have a spreadsheet which calculates the reaction, deflection and slope of a HDPE pipeline as it is being flooded to the seabed for a given water depth. There is 7 no. simultaneous equations which have to be solved in order to obtain the results.
My issue is that the solve block is very sensitive to the guess values, and I often find myself tweaking them until the solve block returns a solution which can be extremely tedious. - Changing Ra to 50 in this instance.
So my question is, can this method be improved and could the equations be solved symbolically?
Cheers,
Mike
Solved! Go to Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
However, when I solve symbolically I am not getting the same reaction forces as the numerical solution, which doesn't seem correct.
Here's a different formulation using a solve block only for L1 and L2. The same results are obtained as solving for all 7 parameters at once.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Mike Armstrong wrote:
However, when I solve symbolically I am not getting the same reaction forces as the numerical solution, which doesn't seem correct.
Here's a different formulation using a solve block only for L1 and L2. The same results are obtained as solving for all 7 parameters at once.
Alan
Superb work Alan. Thank you for all your effort.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
I managed to copy your method and got similar results. So as you previously mentioned I will have to go back to basics and look were the formulae came from.

Attached in M11 format also.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Following on from this I started to compare the answers from the numerical solve block to the answers yielded by the symbolic approach.
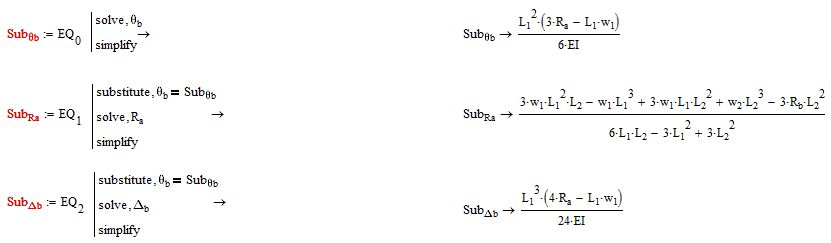
I compared the above three formulas and got the following:
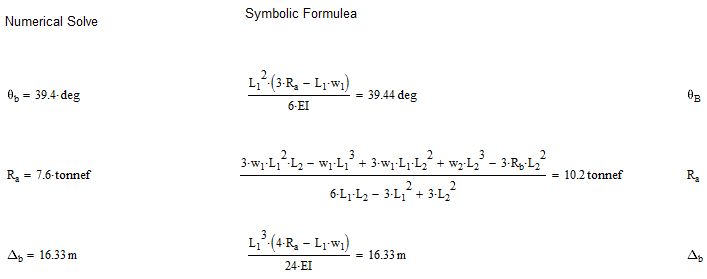
That seems to indicate that the issue is with either Rb or L2, as Omega(b) and Delta(b) are the same.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe it is time to start again with it.
I think you are probably right. Given this mistake, I wouldn't assume that there are no other mistakes higher up the worksheet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the assignment of symbolic results to variables is not supported anymore).
Sure it is.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
. I believe the signs are correct as the deflection and slope graphs in the attached sheet visually look correct.
Mike
You can change the initial guesses to get different outputs with the deflection and slope graphs being essentially unchanged! I'm afraid it's as Andy, Richard and Luc are saying: you are missing a seventh independent equation.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
You can change the initial guesses to get different outputs with the deflection and slope graphs being essentially unchanged! I'm afraid it's as Andy, Richard and Luc are saying: you are missing a seventh independent equation.
Alan
Hi Alan,
Well spotted.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
MikeArmstrong wrote:
A Westerman wrote:
Hi Mike,
I'm not sure, but do you have 7 independent equations?
I've read through the attached & I can't see an obvious error.
looks like equations 5 & 7 can be manipulated to give equation 6.
Hope this helps
Andy
Hi Alan,
I believe I do have 7 independent equations, but unsure why it cannot be solved symbolically. Still digesting Richards sheet
Mike
Sorry, I meant Andy ![]()
- « Previous
-
- 1
- 2
- Next »





