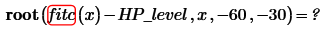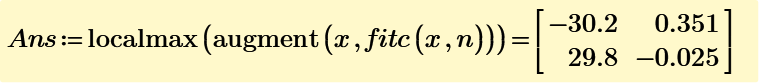Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve for Specific Points Along Interpolated Splined Datasets with MCP9
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve for Specific Points Along Interpolated Splined Datasets with MCP9
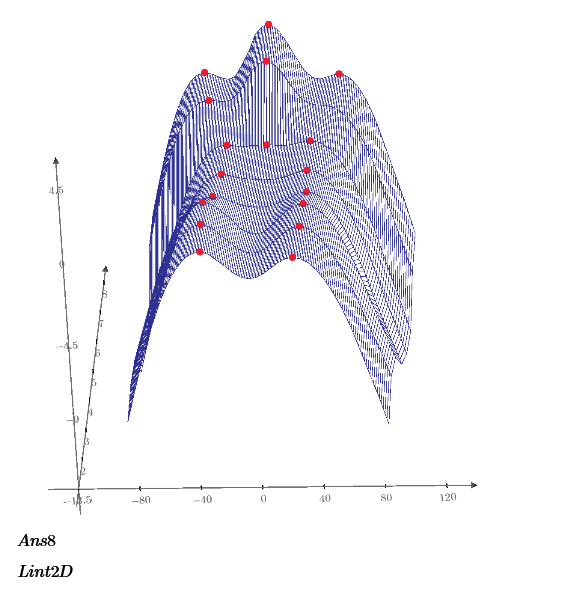
I have several measured data sets. Each dataset will result in a curve with y-axis (ordinate) is its magnitude (in dB) and with x-axis (abscissa) is angle (in degrees). There is fairly large equal spacing between points along their respective abscissa axis, and with accuracy important for this work, interpolation was necessary. I chose to work with a cubic spline to avoid the Runge issue near boundaries.
As you'll see in the attached worksheet, each curve is not perfectly symmetric about zero. Some peak near zero, and some curve's peak is much further away. The goal is to automatically determine an accurate estimate of the angle where the curve's value is 3 dB below the level of the maximum. There should be two such angles - one on either side of zero.
Unfortunately, I'm having difficulty making the symbolic solve and/or solve block to work on just one dataset. But the goal of course is to potentially program this to automatically create a solution for all datasets. I would appreciate some help. Thanks! (newbie alert)
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic solve cannot solve this, as your problem is not described symbolically. You have numeric data.
The solve block will only find one solution, if there is one, and there are ways to control which one it finds by changing the guess value.
Another solver is the root function. Try:
to find the point where fitc(x)=HP_level between -60 and -30.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic solve cannot solve this, as your problem is not described symbolically. You have numeric data.
The solve block will only find one solution, if there is one, and there are ways to control which one it finds by changing the guess value.
Another solver is the root function. Try:
to find the point where fitc(x)=HP_level between -60 and -30.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
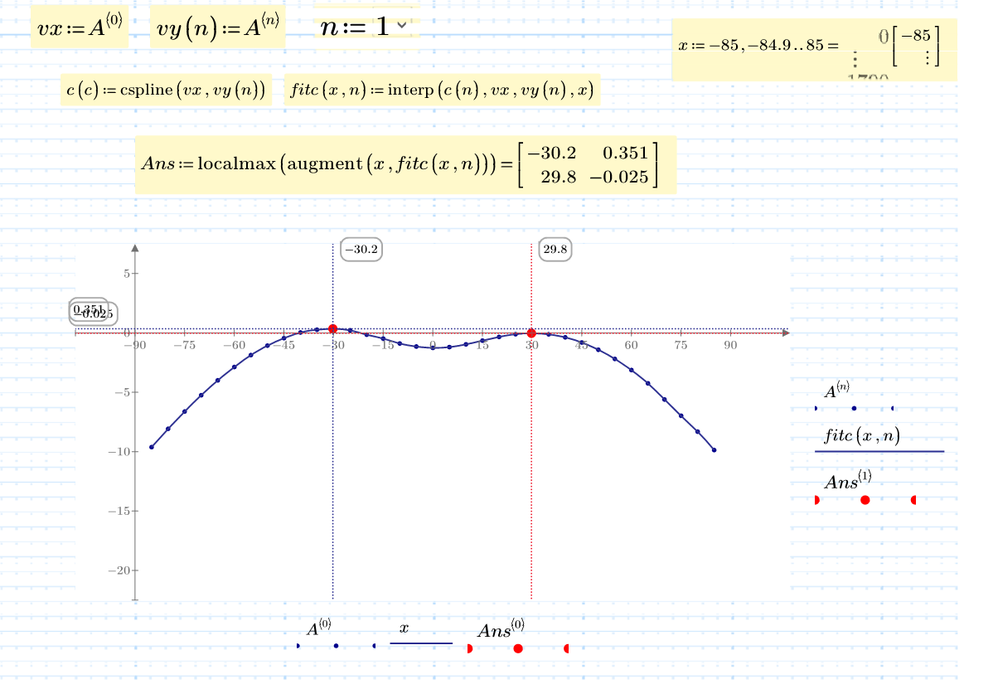
Using localmax function for vector A^(n), you get all max ponts for each DS data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator