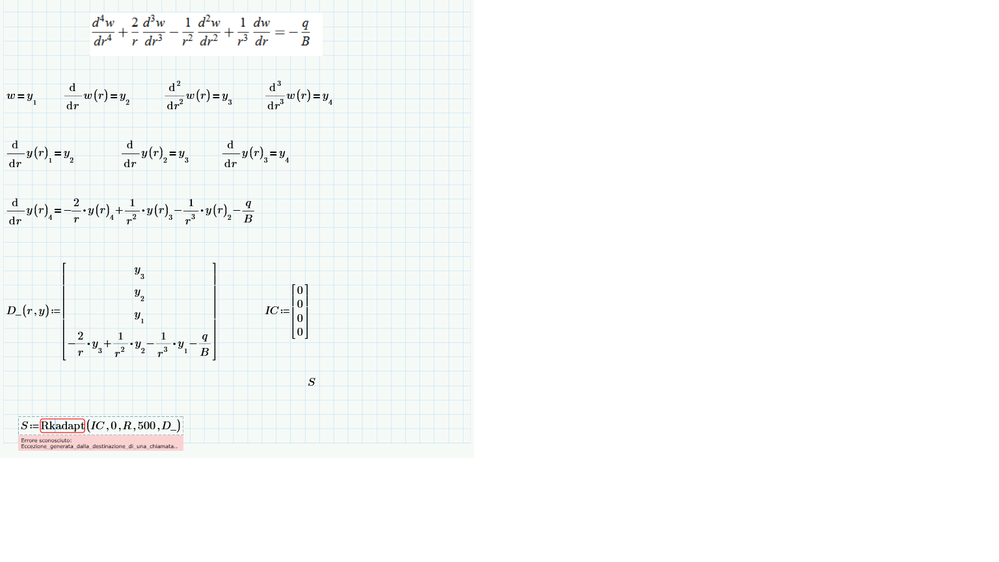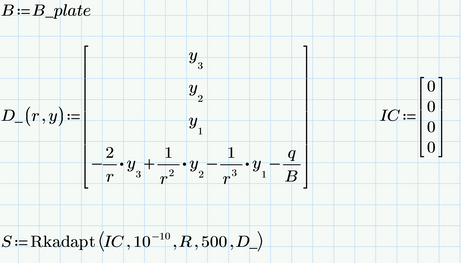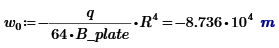Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving 4th degree differential equations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving 4th degree differential equations
Good evening,
I am trying to solve an exercise in MathCad prime 8.0 with the RKadapt function but it return a very unusual error that says "Unknown error: Exception generated by call destination", I have tried to change the function with "Adams" or "rkfixed" and it returns the same error, I have also tried to redefine the equivalences as for example "(d/dr)^2 y(r)1 = y3". Attached there is a screeshot of my work sheet with the differential equation that I need to solve and the procedure that I did.
Thanks to everyone in advance.
Solved! Go to Solution.
- Labels:
-
Mechanical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You forgot to define B (in front of the definition of D_) - Probbably it should be B_plate
This seems to be the reason for the error along with the zero argument I already mentioned.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Please attach your worksheet!
Just a stab in the blue ... try changing the second argument 0 to something positive, like 0.0001.
r=0 yields of course a division by zero! Maybe the reason for the unusual and less helpful error message you get.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have tried your suggestion but it doesn't work. I have attached the entire worksheet but it is written in italian, If you need any clarification just ask me.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What is (capital) R defined to be?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
R is the radius of the disk in the figure in page 14, I have used it in the function because I need to calculate the displacement of the disk in the z direction, which is the solution of the equation from the center of the disk to the end of it.
Thanks again,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You forgot to define B (in front of the definition of D_) - Probbably it should be B_plate
This seems to be the reason for the error along with the zero argument I already mentioned.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you a lot for your help, I have now realized the mistake. Now it shows the graphs as you have shown in the previous answer.
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A couple of funny thing are going on here.
1. If I change Rkadapt to rkfixed I get an error message about incompatible units. This can be corrected by changing the second argument to to 0.001 m.
2. The value of w at R is calculated to be:
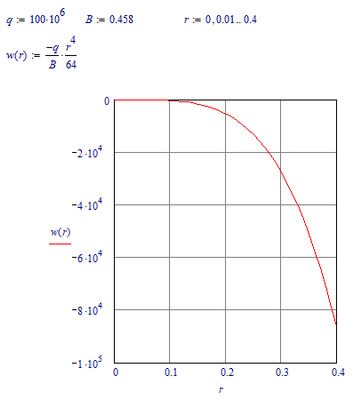
then why does the graph for S<1> versus S<0> show the value at 0.4 m to be near -6*10^-6 ?
Using the (my) symbolic solution, the graph is:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Some hand calculation suggests that
w(r)=(-q/B)*r^4/64
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your help, but I need to obtain the solution using the mathcad solver for this exercise.