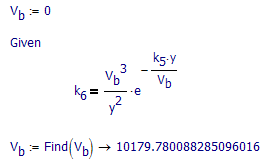Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solving a Polynomial Equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solving a Polynomial Equation
I have been playing around using different methods to solve a polynomial equation and need the help of one of the 'symbolic guru's on here.
I have managed to solve the equation and evaluated numerically, but have the following queries:
- Can I force the symbolic result to return only real values
- Is 'float' required to evaluate the symbolic expression numerically
- Is there a more elegant way to solve this equation.
Thanks,
Mike
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
I have been playing around using different methods to solve a polynomial equation and need the help of one of the 'symbolic guru's on here.
I have managed to solve the equation and evaluated numerically, but have the following queries:
- Can I force the symbolic result to return only real values
Not in an easy and natural way ("assume" does not work for this). See attachment.
- Is 'float' required to evaluate the symbolic expression numerically
I guess to evaluate the LambertW function numerically its a requirement. This function can only be evaluated symbolically and thats the reason you can't use the result of the symbolics directly in numeric evaluations without first symbolically evaluate it by using float and turning it that way into numeric results.
- Is there a more elegant way to solve this equation.
Probably the symbolically evaluated solve block is the better solution. I am not sure why the numeric evaluation fails here.
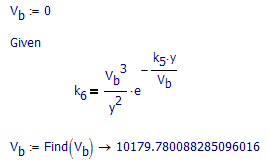
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
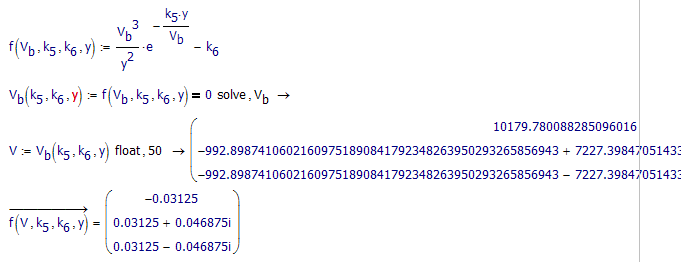
Can I force the symbolic result to return only real values
In general, I think no.
Is 'float' required to evaluate the symbolic expression numerically
You can put a floating point number somewhere in your expression, then you will get a floating point answer (for example, put k.6*1.0). If you do use float then 8 digits is not enough though. Remember that float does not just affect the displayed answer, it affects the precision of the calculations. Check how much error you have in your equality with float 8: about 6,000,000. With float 20 the error is 0.03.
Is there a more elegant way to solve this equation.
I would automate the picking of the real root.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Can I force the symbolic result to return only real valuesIn general, I think no.
Is 'float' required to evaluate the symbolic expression numericallyYou can put a floating point number somewhere in your expression, then you will get a floating point answer (for example, put k.6*1.0). If you do use float then 8 digits is not enough though. Remember that float does not just affect the displayed answer, it affects the precision of the calculations. Check how much error you have in your equality with float 8: about 6,000,000. With float 20 the error is 0.03.
Is there a more elegant way to solve this equation.I would automate the picking of the real root.
Cheers Richard,
I thought you and Werner would be the first to offer an explanation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
I have been playing around using different methods to solve a polynomial equation and need the help of one of the 'symbolic guru's on here.
I have managed to solve the equation and evaluated numerically, but have the following queries:
- Can I force the symbolic result to return only real values
Not in an easy and natural way ("assume" does not work for this). See attachment.
- Is 'float' required to evaluate the symbolic expression numerically
I guess to evaluate the LambertW function numerically its a requirement. This function can only be evaluated symbolically and thats the reason you can't use the result of the symbolics directly in numeric evaluations without first symbolically evaluate it by using float and turning it that way into numeric results.
- Is there a more elegant way to solve this equation.
Probably the symbolically evaluated solve block is the better solution. I am not sure why the numeric evaluation fails here.
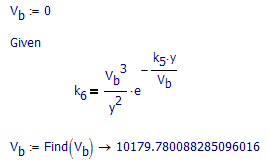
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure why the numeric evaluation fails here.
Big numbers. Change CTOL to 0.1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
I am not sure why the numeric evaluation fails here.
Big numbers. Change CTOL to 0.1.
That only works when the guess value is close to the actual value of V.b.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its seems to work for guess value in the range from 580 to 10^11.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
I am not sure why the numeric evaluation fails here.
Big numbers. Change CTOL to 0.1.
Ah yes! I see. Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Mike Armstrong wrote:
I have been playing around using different methods to solve a polynomial equation and need the help of one of the 'symbolic guru's on here.
I have managed to solve the equation and evaluated numerically, but have the following queries:
- Can I force the symbolic result to return only real values
Not in an easy and natural way ("assume" does not work for this). See attachment.
Why though. That was baffling me all afternoon.
Werner Exinger wrote:
- Is 'float' required to evaluate the symbolic expression numerically
I guess to evaluate the LambertW function numerically its a requirement. This function can only be evaluated symbolically and that's the reason you can't use the result of the symbolic's directly in numeric evaluations without first symbolically evaluate it by using float and turning it that way into numeric results
I get it thanks. Is there a way to assess beforehand if a function can be evaluated numerically?
Thanks for spotted the error with the Minerr example. However, the numerical processor is still dependant on the guess values from the user. Sorry for sounding stupid, but why can the symbolic processor solve it?
Werner Exinger wrote:
- Is there a more elegant way to solve this equation.
Probably the symbolically evaluated solve block is the better solution. I am not sure why the numeric evaluation fails here.
Yes is much neater and it does not rely on the guess value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
Werner Exinger wrote:
Mike Armstrong wrote:
I have been playing around using different methods to solve a polynomial equation and need the help of one of the 'symbolic guru's on here.
I have managed to solve the equation and evaluated numerically, but have the following queries:
- Can I force the symbolic result to return only real values
Not in an easy and natural way ("assume" does not work for this). See attachment.
Why though. That was baffling me all afternoon.
Hard to tell. Mathcads symbolics often is a mere puzzle and it get worse when they switched from Maple to Mupad. Especially the assume keyword very often gets not respected or behaves differently as one might expect.
I see mathcad as a very good all purpose tool and "the" tool when it comes to documentation. An all purpose tool is fair in most part of what it does but probably not top notch in any. So when it comes to refined algorithm and more sophisticated predefined functions, you would rather like Matlab, when symbolics is your main goal, you'd rather jump over to mathematica or Maple.
Mathcad's symbolics is just fair and from time to time when it gets more complicated not even that.
Werner Exinger wrote:
- Is 'float' required to evaluate the symbolic expression numerically
I guess to evaluate the LambertW function numerically its a requirement. This function can only be evaluated symbolically and that's the reason you can't use the result of the symbolic's directly in numeric evaluations without first symbolically evaluate it by using float and turning it that way into numeric results
I get it thanks. Is there a way to assess beforehand if a function can be evaluated numerically?
There is a list of functions which can only be evaluated symbolically in the help pages. There was a thread quite some time ago, where someone had asked if it would be possible to create a wrapper function so those function could then be evaluated numerically, too. As far as I remember there was no really satisfactory solution but Richard supplied a way to do wht the poster asked in Mathcad 11 (which was the version the OP used).
Thanks for spotted the error with the Minerr example. However, the numerical processor is still dependant on the guess values from the user. Sorry for sounding stupid, but why can the symbolic processor solve it?
Yes the numeric algorithms need a guess value and also considers the value of CTOL, as Richard had pointed out.
The symbolic solver does not use numeric approximation algorithms and therefore needs no guess value and may behave differently. And the symbolic solver is called when a solve block is evaluated symbolically. You will notice that you can't change the algoriothm used with the right click menu when you evaluate Find() symbolically.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Superb explanation as usual.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, forgot to mention. I like your REALONLY function ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
Oh, forgot to mention. I like your REALONLY function
Unfortunately it doesn't work directly with the result of your function V.b(k.5,k.6,y).
You have it to evaluate symbolically with float and assign it a global variable first.
I tried to do the same inside the function with a local variable - but to no avail. 😞
One thing which still baffles me is why there is that difference between using the symbolic solver (3 results and using the LambertW function) and evaluating the solve block symbolically (just one real result and the LambertW is already evaluated numerically like we had to do with float otherwise).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Mike Armstrong wrote:
Oh, forgot to mention. I like your REALONLY function
Unfortunately it doesn't work directly with the result of your function V.b(k.5,k.6,y).
You have it to evaluate symbolically with float and assign it a global variable first.
I tried to do the same inside the function with a local variable - but to no avail. 😞
That's because of the limitations with the function itself, isn't it?
One thing which still baffles me is why there is that difference between using the symbolic solver (3 results and using the LambertW function) and evaluating the solve block symbolically (just one real result and the LambertW is already evaluated numerically like we had to do with float otherwise).
Does this have something to do with the solve and find commands?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One thing which still baffles me is why there is that difference between using the symbolic solver (3 results and using the LambertW function) and evaluating the solve block symbolically (just one real result and the LambertW is already evaluated numerically like we had to do with float otherwise).
Does this have something to do with the solve and find commands?
It has something to do with the numeric assignment to a function.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats interesting. So when Mupad is forced to solve symbolically first an then insert the values because the solve expression is assigned a function we get three results, when the values are put in first we just get one.!?
I also tried how good the solutions are - rather poor!
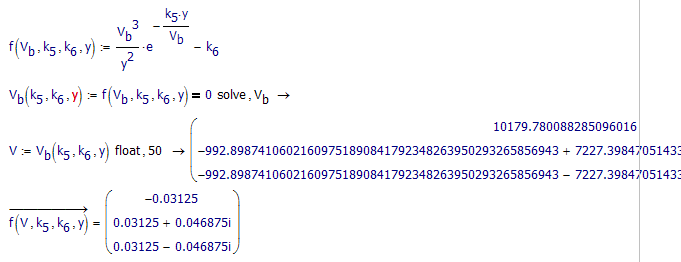
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It certainly seems that way
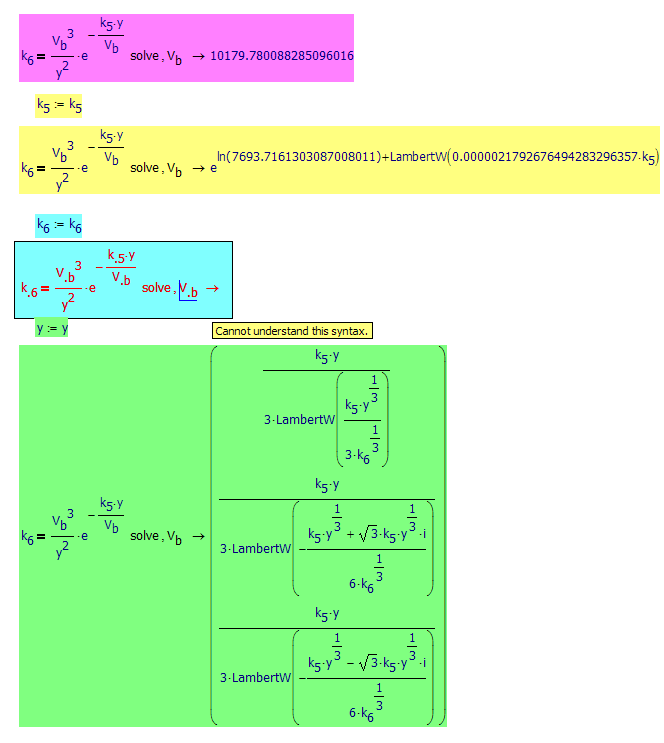
Not sure what to make of that error though!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Strange error, indeed.
The multiple solutions stem from taking the third root of V.b.
Replacing V.b by its third root gives us the following
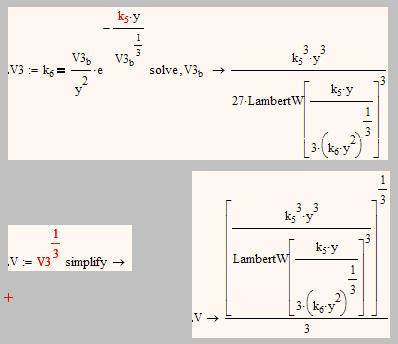
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Thats interesting. So when Mupad is forced to solve symbolically first an then insert the values because the solve expression is assigned a function we get three results, when the values are put in first we just get one.!?
I also tried how good the solutions are - rather poor!
I am struggling to reply to the correct post now ![]()
However, here will do. I think I have got my head around the cause of receiving different symbolic results, but the question is, why? I don't see any logical reason we Mupad returns 3 results because the numeric assignment is passed to a function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
One thing which still baffles me is why there is that difference between using the symbolic solver (3 results and using the LambertW function) and evaluating the solve block symbolically (just one real result and the LambertW is already evaluated numerically like we had to do with float otherwise).
Does this have something to do with the solve and find commands?
It has something to do with the numeric assignment to a function.
Doesn't make sense at all though. Why is it not the case when the numeric assignment 'find' is applied to a function?
Message was edited by: Mike Armstrong
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems that the solve block picks up on the numeric definitions even if they are function arguments. If y is not defined before the solve block you get the three solutions. If k5 and/or k6 are not defined before the solve block it fails though, unlike solve.
The mysteries of Mathcad symbolic math!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately it doesn't work directly with the result of your function V.b(k.5,k.6,y).
You have it to evaluate symbolically with float and assign it a global variable first.
I tried to do the same inside the function with a local variable - but to no avail. 😞
That's because of the limitations with the function itself, isn't it?
It has to do with the fact that I cannot simulate numeric inline evaluation in a program. See attached sheet.
One thing which still baffles me is why there is that difference between using the symbolic solver (3 results and using the LambertW function) and evaluating the solve block symbolically (just one real result and the LambertW is already evaluated numerically like we had to do with float otherwise).
Does this have something to do with the solve and find commands?
Not sure. I thought that the same symbolics algorithms would be used in both cases when we do symbolic evaluation - obviously thats not true.
Here I did some poking around trying to make the results of the LamberW function available to the numerics. Again no success to build a wrapper function.
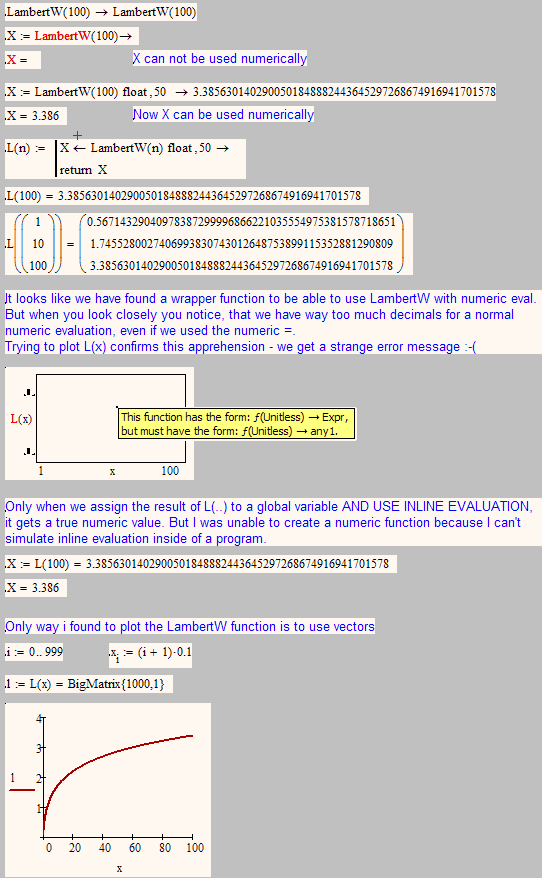
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Courtesy of Tom.
![]()
So the solution not to use the built-in function altogether and write your own - hmmm.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nicely done guys. Some great information provided on here which will certainly help us too.