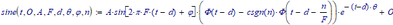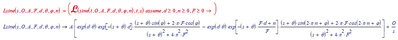Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Square, Sine and PiceWise Linear Waves/Functions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Square, Sine and PiceWise Linear Waves/Functions
Hello Dear Friends,
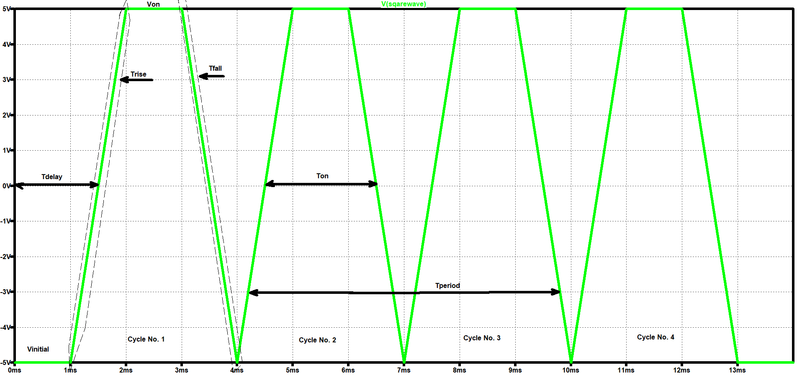
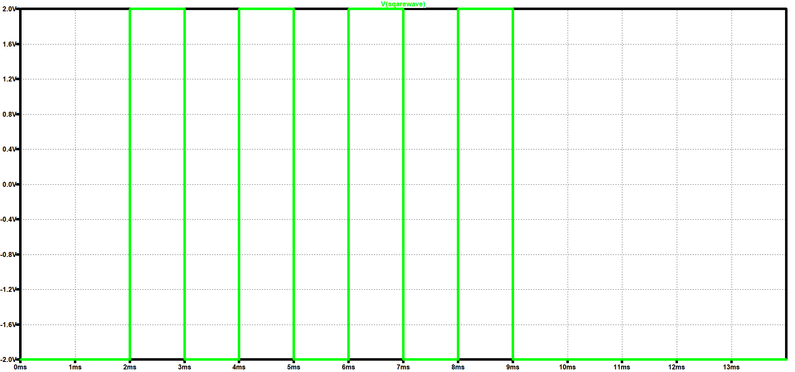
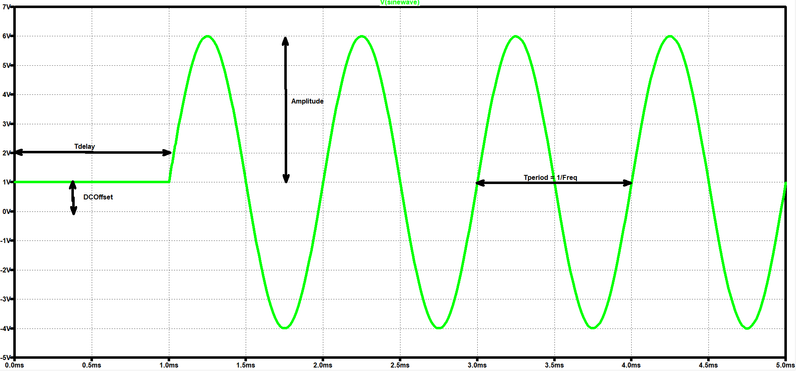
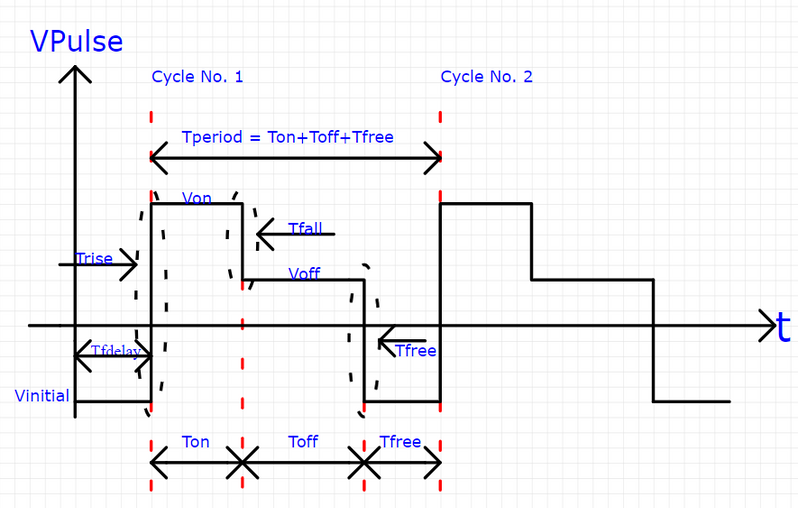
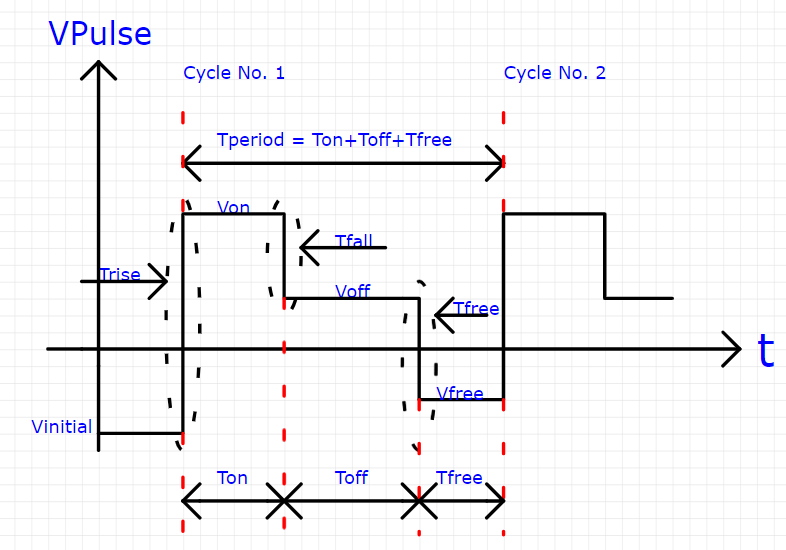
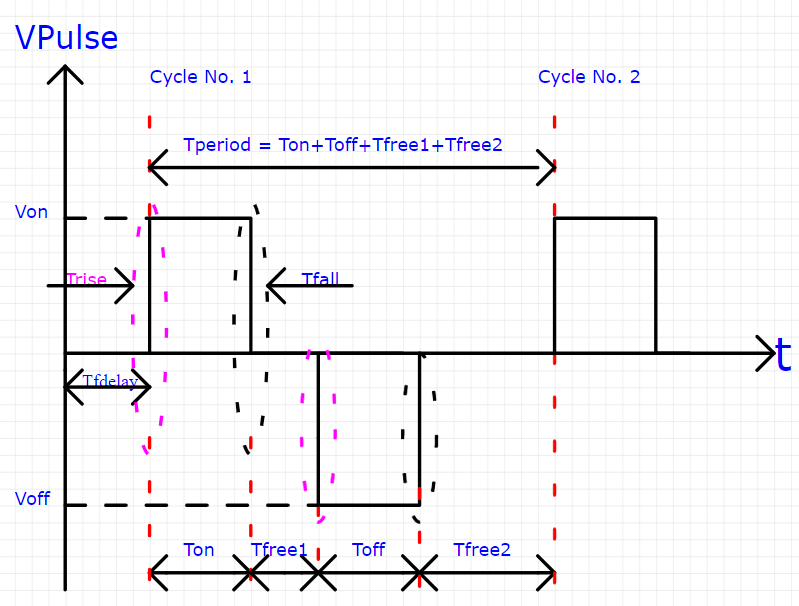
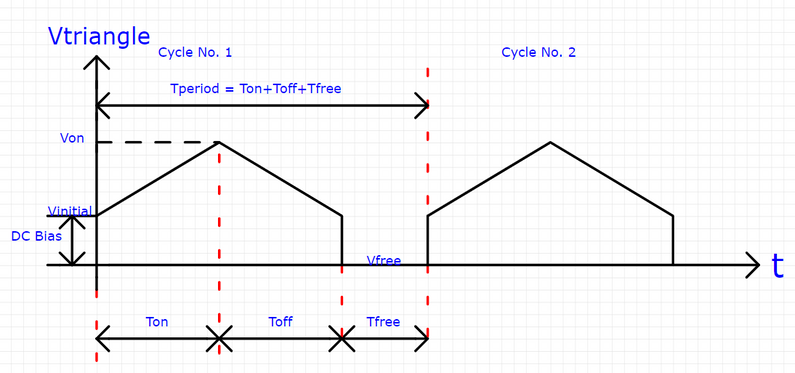
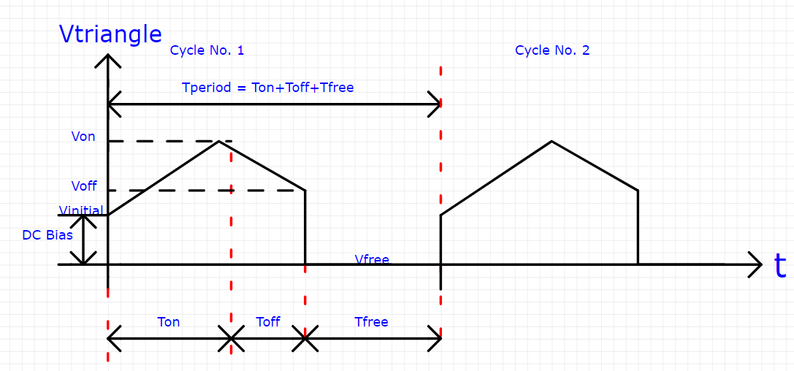
Do you have any idea how to implement in Mathcad 15 the functions that generate the following graphs shown below?
Case 1:
And if I change the parameters:
Case 2:
a)
b)
c)
Case 3:
Thank you.
Best regards.
- Labels:
-
Electrical_Engineering
-
Programming
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are many ways that lead to Rome (or many another city).
What is your purpose with those functions:
- Do you just want to plot them?
- Do you need them to work numerically only?
- Are you going to use them symbolically?
- Do you intend to use them in (inverse) Fourier and/or Laplace transforms?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All 4 points listed by you, if it is possible.
The first 3 would be the main ones.
If it exists symbolically then by customizing the values it can be evaluated numerically, and then it can be plotted. But I have no idea yet how to build these functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All of your examples except this
can be simply achieved using either the Linterp or sine function along with some time limit constraints.
Let's see (from an Amethyst level member) a sheet at least showing your attempts.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do not think that the rank can be an argument that resolves things or the rank is protected from the problems or questions:))), neither diploma of a faculty does not make you a successful/great engineer:) or at least an engineer who has unanswered questions.
Until now, whatever topic I opened I posted what I have done so far.
For this thread, I do not have a Mathcad file because I do not know how these functions can be realized, how they can be thought.
What I want to obtain is some function(s) in which I input these parameters (Vinitial, Von, Tdelay, Trise, Tfall, Ton, Tperiod, Ncycles) and so on for the other shapes/graphs within this topic, and at the end of the story, these functions help me to reach at the output graphs, as shown in the figures in this topic.
I don't think that's that simple to do. This is the reason for which I posted this message.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i have seen this done many times before on the old mathsoft forum. i don't recall how to do it though. i'm sure some of the current forum members would know how. unfortunately, it's not something built in to mathcad that is easy to access. you pretty much have to do it yourself. it was something i was hoping would eventually be implemented but never was. now ptc killed classic mathcad. so who knows what they will do with prime.
one obvious use of this that no one ever noticed was forcing functions for the ode solver. so mass spring damper systems. it would have been nice to have easy to access wave forms to load the system with.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now come on.
Don't tell me that you are incapable of writing a function that produces a sine wave with given frequency, amplitude and offset as a function of time. A slight modification would add the starting phase, and with a little ingenuity you should be able to have it end after a certain number of periods of the sine.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
sine and cosine waves of course are built in. i meant other types of wave forms. it would be nice to have a built in drop down box of all sorts of periodic waves that you would just specify the parameter to. really have no idea why this was neglected in the program in the first place.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes @Fred_Kohlhepp @prop_design
The sine and cosine waves were just for example to shown how to arrive with the case 2) point c).
It's not really about sine and cosine waves, but as you saw and intuited very well...it's about other types of waves like case 1 and case 3 (and perhaps other types of waves, more or less general types that are extensively used in various domains like electronics engineering).
And how to parameterize such waves to make life easier.
Good point.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
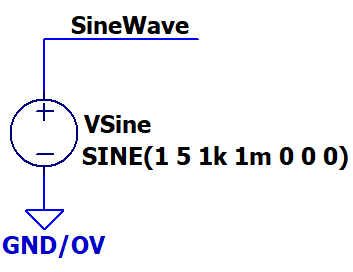
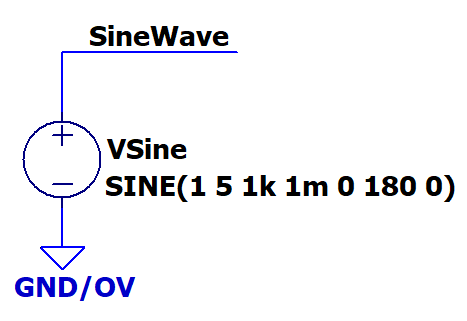
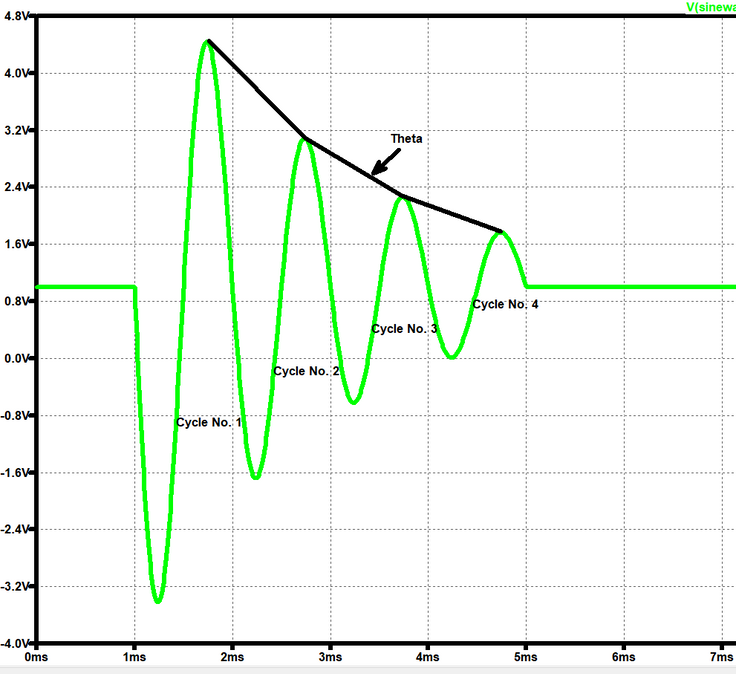
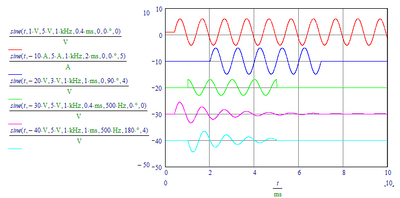
Well, here is a first shot, for the sine wave(s). Parameters as listed in your picture.
It's Laplace transformable:
And of course it plots all Spice's sine wave variants:
Evidently, you can apply units as you like.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
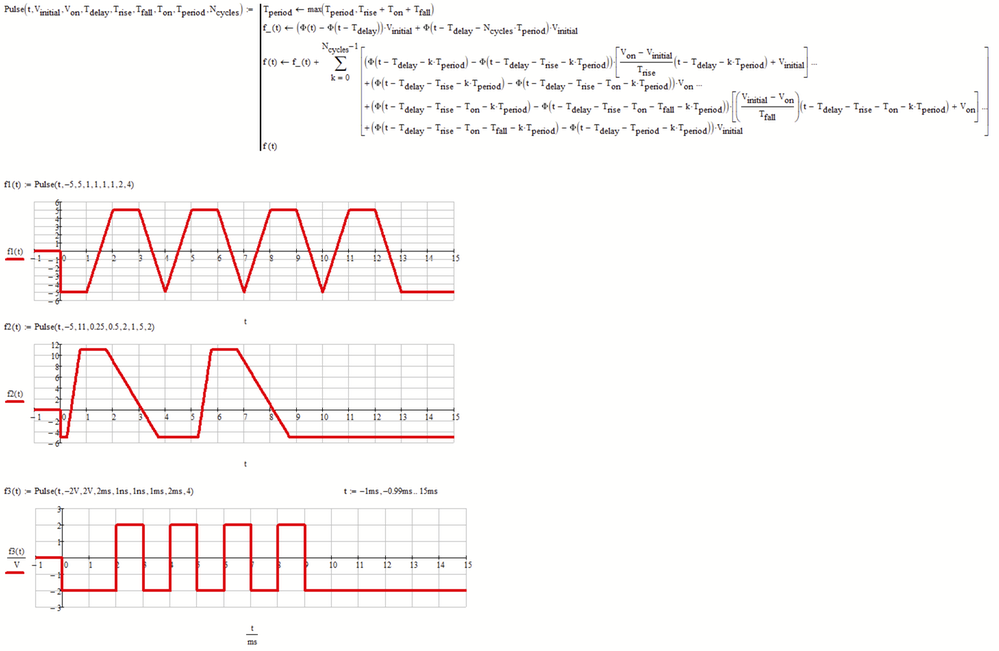
Here is a function for the pulse wave for you to start with.
The function takes the same arguments in the same order as shown in your screenshot. However, the times that you show with arrows in the first picture "for clarity" seem to be quite inaccurate and misleading.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
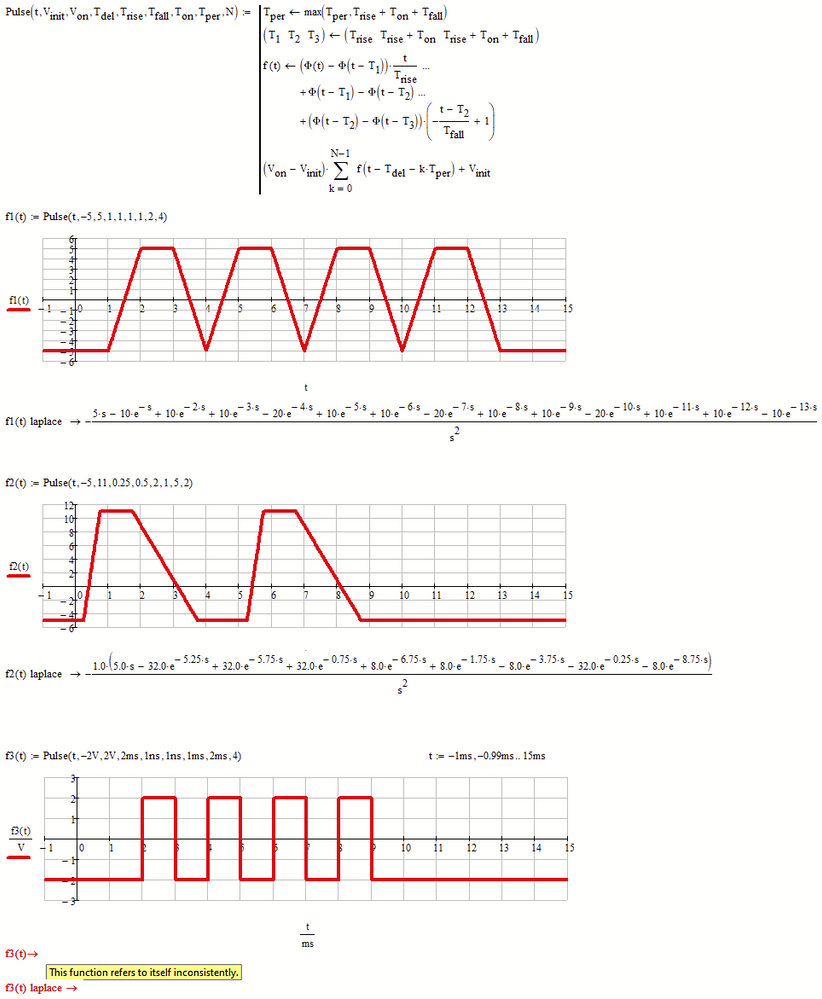
Here is a more compact version of the function posted above.As you can see in the last example, symbolic operations won't work when used with units!EDIT: See below.
EDIT My fault. The error occurs because I redefined t to be the range for plotting, should have used a different variable name (normally I use "t." in such cases as it looks like a normal "t".
So you see that the symbolic also works with units, but I can image that a useful result often will be demanded too much. As you should know the symbolic does not know anything about units and treats them as unknowns.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
😍
Good.
Thank you very much.
I dare to ask if the following options would be possible:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems that in your pics you are using Tfree for two different things!
The more different parts your signal should consist of, the more summands you would have to add to f(t) in the function and the more arguments your function will get.
Unfortunately we are not allowed to create functions in Mathcad which can be called with a variable number of arguments. So it may be a better option to provide vectors as arguments to the function. The first vector could consist of the times (T.1, T.2 etc in my function), the second may indicate the signal value (constant or ramp; nor sure how to implement that).
It should be easy to create that kind of function for the piecewise linear function PWL you showed in your initial post - first vector consists of times, second vector of the associated values.
Give it a try and come back here if you got stuck.
EDIT: Actually all the signals you showed in your last post could be created by a PWL function by adding T.delay, T.period and N.cycles as arguments to repeat the signal a couple of times. The times you would have to provide would not be T.rise, T.on, T.fall, etc. but rather the sums of those. You may also consider to provide the times as given in the vector and let your function do the summing - similar to what I did in the second version of my function when I calculated T.1, T.2, etc. just to save space.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All in one without reference files: Signals, data, Fourier analysis, sampling, and reconstruction of the signal with Shannon's theorem ( To reduce processing times, you must reduce N1_, for example, N1_ = 25.). See attached file.