- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
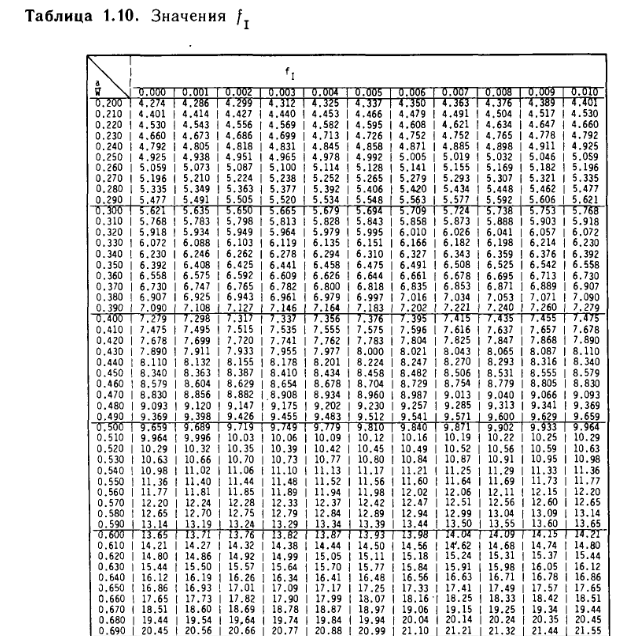
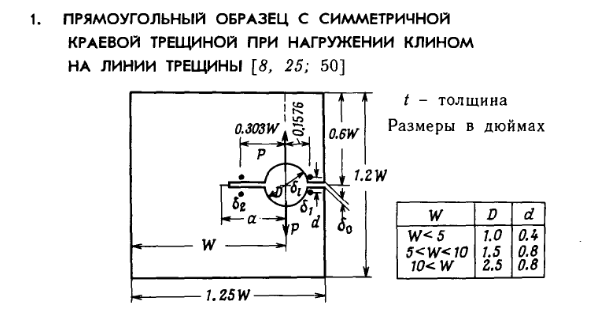
Stopped at a tabular values from the handbook
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Stopped at a tabular values from the handbook
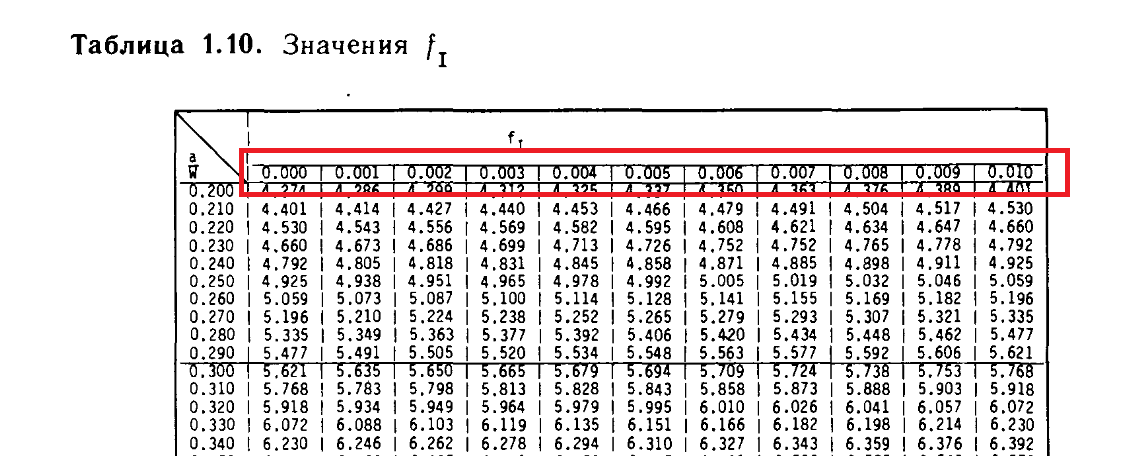
For the solution of one of tasks I work with the handbook by author Y. Murakami - "Stress intensity factors handbook", Vol 1. I try to deal with tabular values for a choice of correction coefficient "f_1"which enters a formula for coefficient of intensity factors "K_1". Correction coefficient (on the formula given in the reference book) depends only on the "alpha" variable which represents itself the relation of the geometrical sizes, however at a choice of tabular value for correction coefficient of "f_1" one more numerical scale appears there (values in it change from size 0.000 and to 0.010). What mean these values from 0.000-0.010? I looked at all first volume of this handbook, and also reference article [8], [25], [50], but didn't find a mention of it there about these values. There are any ideas? Perhaps I missed something.


Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
VladimirN. wrote:
For the solution of one of tasks I work with the handbook by author Y. Murakami - "Stress intensity factors handbook", Vol 1. I try to deal with tabular values for a choice of correction coefficient "f_1"which enters a formula for coefficient of intensity factors "K_1". Correction coefficient (on the formula given in the reference book) depends only on the "alpha" variable which represents itself the relation of the geometrical sizes, however at a choice of tabular value for correction coefficient of "f_1" one more numerical scale appears there (values in it change from size 0.000 and to 0.010). What mean these values from 0.000-0.010? I looked at all first volume of this handbook, and also reference article [8], [25], [50], but didn't find a mention of it there about these values. There are any ideas? Perhaps I missed something.
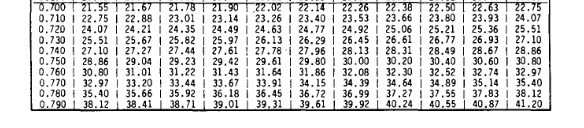
Is it just the 3rd decimal digit? I notice that, despite there being 3 digits in the a/W column, they numbers all end in zero, whilst the column headers are zero except for the 3rd digit. The last column is an exception, as it looks like it gives the same value as the first value (0.000 column) in the next row (eg, 0.290/0.010 = 5.621 and 0.300/0.000 = 5.621)
Quod erat demonstrandum and all that ...
Stuart

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VladimirN. wrote:
For the solution of one of tasks I work with the handbook by author Y. Murakami - "Stress intensity factors handbook", Vol 1. I try to deal with tabular values for a choice of correction coefficient "f_1"which enters a formula for coefficient of intensity factors "K_1". Correction coefficient (on the formula given in the reference book) depends only on the "alpha" variable which represents itself the relation of the geometrical sizes, however at a choice of tabular value for correction coefficient of "f_1" one more numerical scale appears there (values in it change from size 0.000 and to 0.010). What mean these values from 0.000-0.010? I looked at all first volume of this handbook, and also reference article [8], [25], [50], but didn't find a mention of it there about these values. There are any ideas? Perhaps I missed something.
Is it just the 3rd decimal digit? I notice that, despite there being 3 digits in the a/W column, they numbers all end in zero, whilst the column headers are zero except for the 3rd digit. The last column is an exception, as it looks like it gives the same value as the first value (0.000 column) in the next row (eg, 0.290/0.010 = 5.621 and 0.300/0.000 = 5.621)
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
VladimirN. wrote:
For the solution of one of tasks I work with the handbook by author Y. Murakami - "Stress intensity factors handbook", Vol 1. I try to deal with tabular values for a choice of correction coefficient "f_1"which enters a formula for coefficient of intensity factors "K_1". Correction coefficient (on the formula given in the reference book) depends only on the "alpha" variable which represents itself the relation of the geometrical sizes, however at a choice of tabular value for correction coefficient of "f_1" one more numerical scale appears there (values in it change from size 0.000 and to 0.010). What mean these values from 0.000-0.010? I looked at all first volume of this handbook, and also reference article [8], [25], [50], but didn't find a mention of it there about these values. There are any ideas? Perhaps I missed something.
Is it just the 3rd decimal digit? I notice that, despite there being 3 digits in the a/W column, they numbers all end in zero, whilst the column headers are zero except for the 3rd digit. The last column is an exception, as it looks like it gives the same value as the first value (0.000 column) in the next row (eg, 0.290/0.010 = 5.621 and 0.300/0.000 = 5.621)
Quod erat demonstrandum and all that ...
Stuart

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Incidentally, the handbook does not have the whole table for "f_1", but only the value to a value of 0.790. While at the same time said formula for "f_1" operates with an accuracy of 0.5% for values between 0.2 and 1.0.
The area allocated on a screenshot works with use of local definition only in the matrix function or it can be set/defined even earlier?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VladimirN. wrote:
The area allocated on a screenshot works with use of local definition only in the matrix function or it can be set/defined even earlier?
Hi Vladimir,
The matrix function will work with a predefined function. I like to use local functions if they're simple and I'm only going to use them once
I designed matrix as a direct replacement for the built-in matrix function as I got fed up with rescaling things to cater for the implied integer grid, and I also wanted a function that would work with string functions in earlier versions of Mathcad.
I've got a related function Matrix that returns the 'x' and 'y' vectors as well.


Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Values in the table are from 0.000 desviation from the formula for f.I(alpha) (and the first column are the exact values for the expression) and some degree of compliance which vary from 0.000 to 0.010. I guess that this is according ref [8]:
" ... It is the purpose of this report to present new expressions which are at least as accurate as those in E 399-74, and which cover much wider ranges of a/W: for the three-point bend specimen from 0 to 1; for the compact specimen from 0.2 to 1 ..."
This correction is made just because " ... It is explicitly stated in the standard, however, that these expressions should not be used outside the range of relative crack length a/W from 0.45 to 0.55. ..."
So, are the correction for the expressed formula f.I(alpha)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
Values in the table are from 0.000 desviation from the formula for f.I(alpha) (and the first column are the exact values for the expression) and some degree of compliance which vary from 0.000 to 0.010.
I'm not sure that's the case, Alvaro. I think it's just a compact way of displaying the data ... rather like good, old-fashioned log tables.
I guess that this is according ref [8]:
Do you mean Ref [25]?
...I guess that this is according ref [8]: " ... It is the purpose of this report to present new expressions which are at least as accurate as those in E 399-74, and which cover much wider ranges of a/W: for the three-point bend specimen from 0 to 1; for the compact specimen from 0.2 to 1 ..."
This correction is made just because " ... It is explicitly stated in the standard, however, that these expressions should not be used outside the range of relative crack length a/W from 0.45 to 0.55. ..."
So, are the correction for the expressed formula f.I(alpha)
The introduction also states "While this range is sufficient for the purpose of E 399, the same specimen types are often used for other purposes over a much wider range of a/W; for example, in the study of fatigue crack growth". From my reading, this makes it more of an expansion than a correction. The difference between the 2.90 and 2.95 values is about 1 %; I can't see anything in the text or Table 1 that indicates the 2-digit values are any more accurate than the 3-digit values.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So we have a split decision here? ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
VladimirN. wrote:
So we have a split decision here?
Нет, мы должны уладить это, как мужчины. mano a mano. Pistols at dawn ... unheated water pistols, that is, on a frigid Moscow winter day! ![]()
Regardless of the reason why the tabulation occurred, my worksheet makes it clear that the values across the top are the 3rd decimal digit - evaluating the function under this assumption agrees with the printed table.
Stuart;
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No Split decision. Stuart have the match here. Even "mano a mano" can be interpreted also as draw (tablas), it was maybe un cara a cara.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
No Split decision. Stuart have the match here. Even "mano a mano" can be interpreted also as draw (tablas), it was maybe un cara a cara.
I'll stick with "mano a mano" then, Alvaro, if it's a draw! ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is the main object of ne chapter of the book
Сайт книги Теплотехнические этюды с Excel, Mathcad и Интернет
In English
Thermal Engineering studies with Excel, Mathcad and Internet