Symbolic solution to filter magnitude frequency response

[DaveWooff]

Hi all,

please see attached.

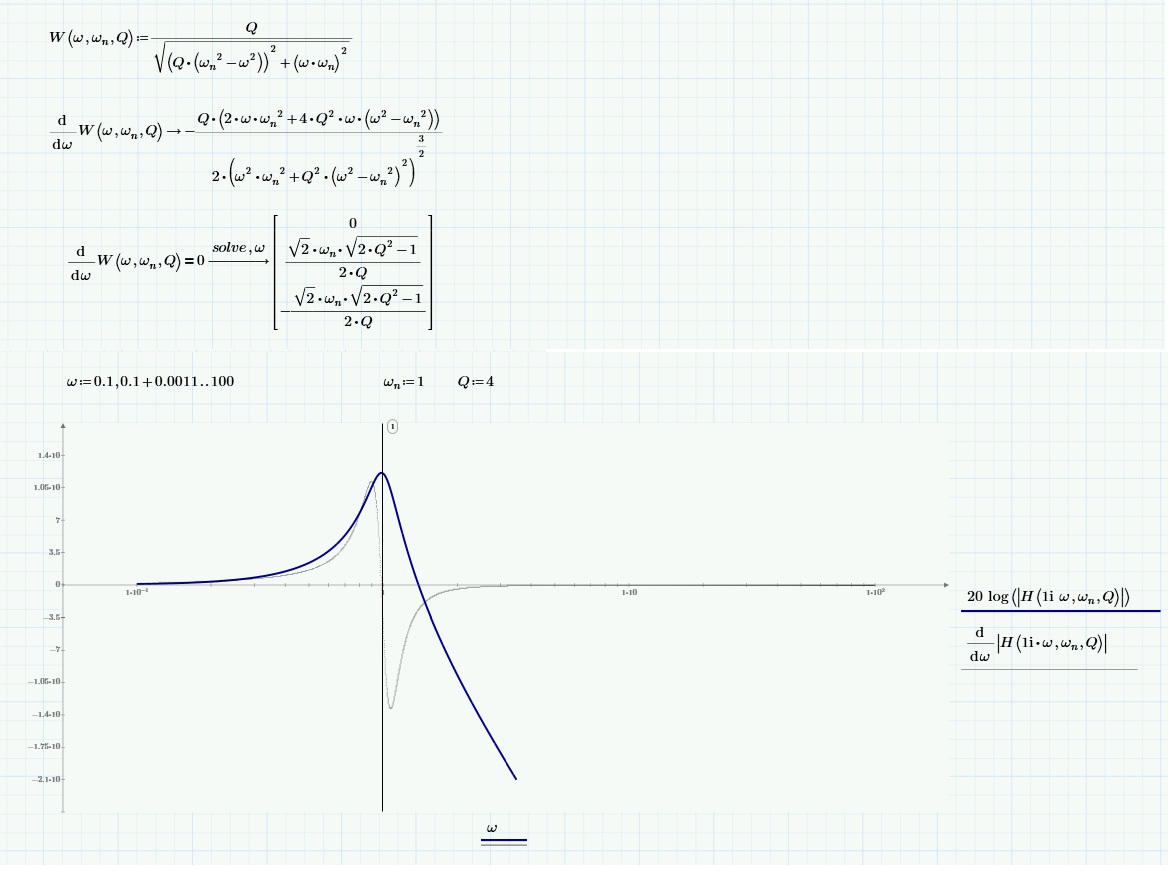
I am attempting to derive what I thought would be a simple enough equation to describe the maxima and/or minima of a "filter" function magnitude response.  The example is a simplified version of my original problem and although in this case the answer is very obvious (w = 1), my original problem did not have so obvious an answer,  And also, although I can easily plot the response, I would like to establish the design equations to allow me to work backwards from a requirement to a solution in equation form.

In the worksheet, the symbolic solution seems to fail.  I specify the function H(s) and then substitute s = 1i.w to obtain continuous frequency response.  I suspect the problem is complicated by the use of the |magnitude| function which might make symbolic solution difficult - that's my guess at why this doesn't seem to work.  If there is a better way then please let me know!  I have been staring at this on and off for a few days so might be missing the obvious.

Thanks in advance,

D

[-MFra-]

[DaveWooff]

thank you for your reply F.M.

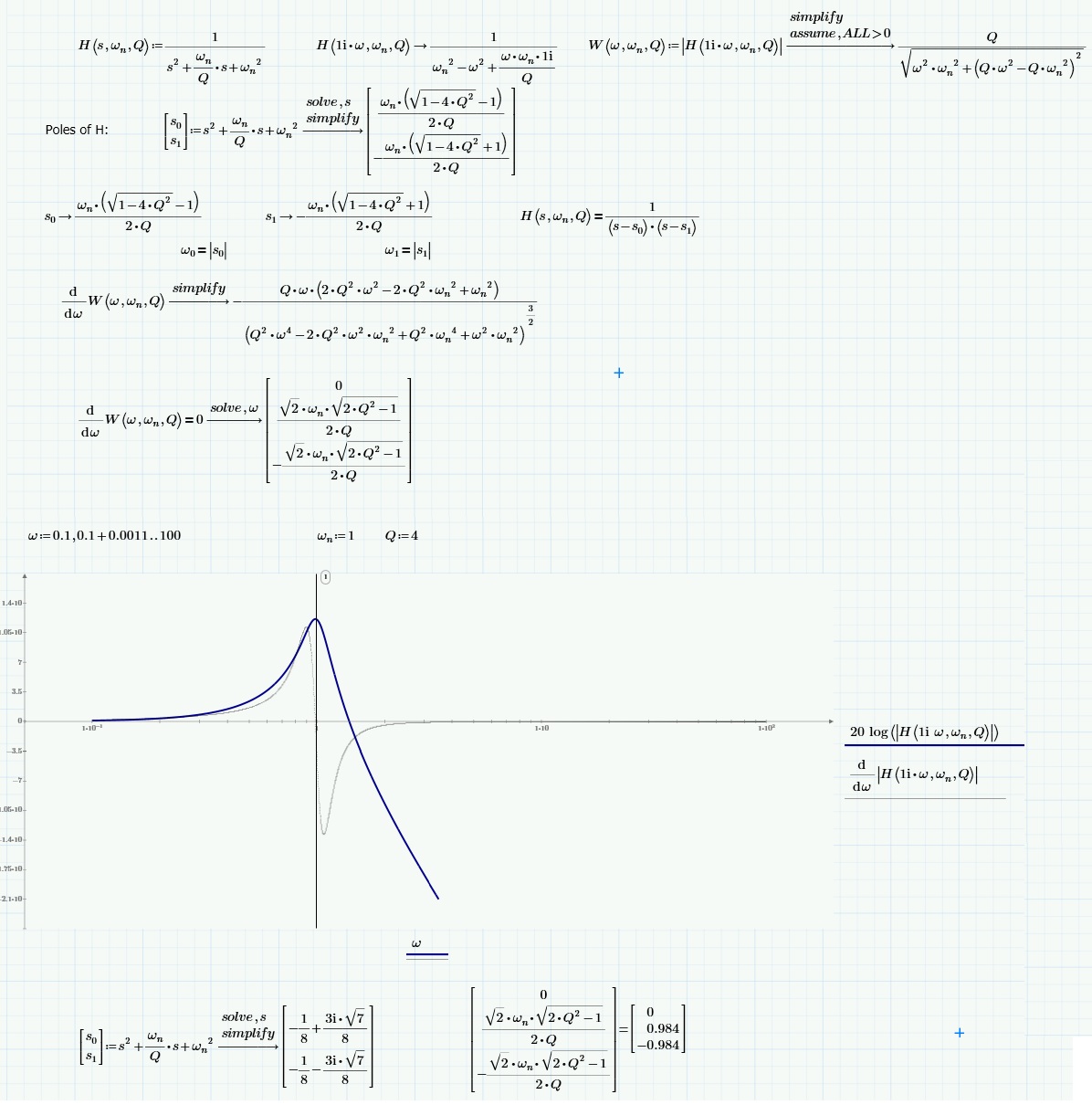
The resulting values are complex.  Since I am evaluating H(s) on the imaginary axis of the s-plane, I expect real values of w.  If I substitute the example values of wn (1) and Q (4) shown in the worksheet, I get [0.125i, 0.992+0.125i, -0.992_0.125i].  The real positive value of w which produces a peak in H(jw) is actually ~0.984.

[-MFra-]

The calculation of the module of the transfer function is not complete, for this reason the results were incorrect.

[DaveWooff]

That's great, thank you.  Is it not sad though that you had to explain the magnitude calculation to Prime before it could deal with the rest?  I guess it was asking too much (especially since it appeared to give misleading results)?  (Edit) perhaps I have to provide Prime with more info or help in the form of an assumption into the symbolic solver.

[-MFra- · Accepted solution]

Now, it seems to me that everything is OK.

[DaveWooff]

I had attempted something similar with "assume w = real" (which didn't work).  Your experience with Mathcad helped me a lot.  Thank you again.

[LouP]

One thing that may help with these types of problems is to define and use the squared magnitude function instead of the magnitude (as a function of w). The squared magnitude is a rational function of w, and has no radicals. This may ease the task on the symbolic engine in some cases where the magnitude function doesn't solve symbolically. This is strictly a generic comment, as I haven't tried it on on this example. I have almost always used the squared magnitude when setting up system function calculations and the magnitude is of interest. I try to avoid radicals whenever possible in symbolics, as they have multiple solutions in general, and the algebra can get quite complex(no pun intended).

Lou

[DaveWooff]

Thank you, but what do you mean by the squared magnitude function?

[LouP]

Just the square of the magnitude function. For H(s) = 1/(s+1), we have H(w) = 1/(jw+1), |H(w)| = 1/sqrt(1+w^2). The magnitude squared is |H(w)|^2 = 1/(1+w^2), which is a rational algebraic function. |x + jy|^2 = x^2 + y^2; no sqrt required.

[LouP]

Another comment triggered by some of your earlier posts on differentiating the magnitude function. The magnitude function directly (as a function of w) has cusps where the magnitude has simple zeroes, and the derivative does not exist at these points, hence symbolic operations may be problematic. Conversely, the square of the magnitude (see example in preceding post) is an analytic function, and the derivative is well defined everywhere (except at poles of course).

[Fred_Kohlhepp]