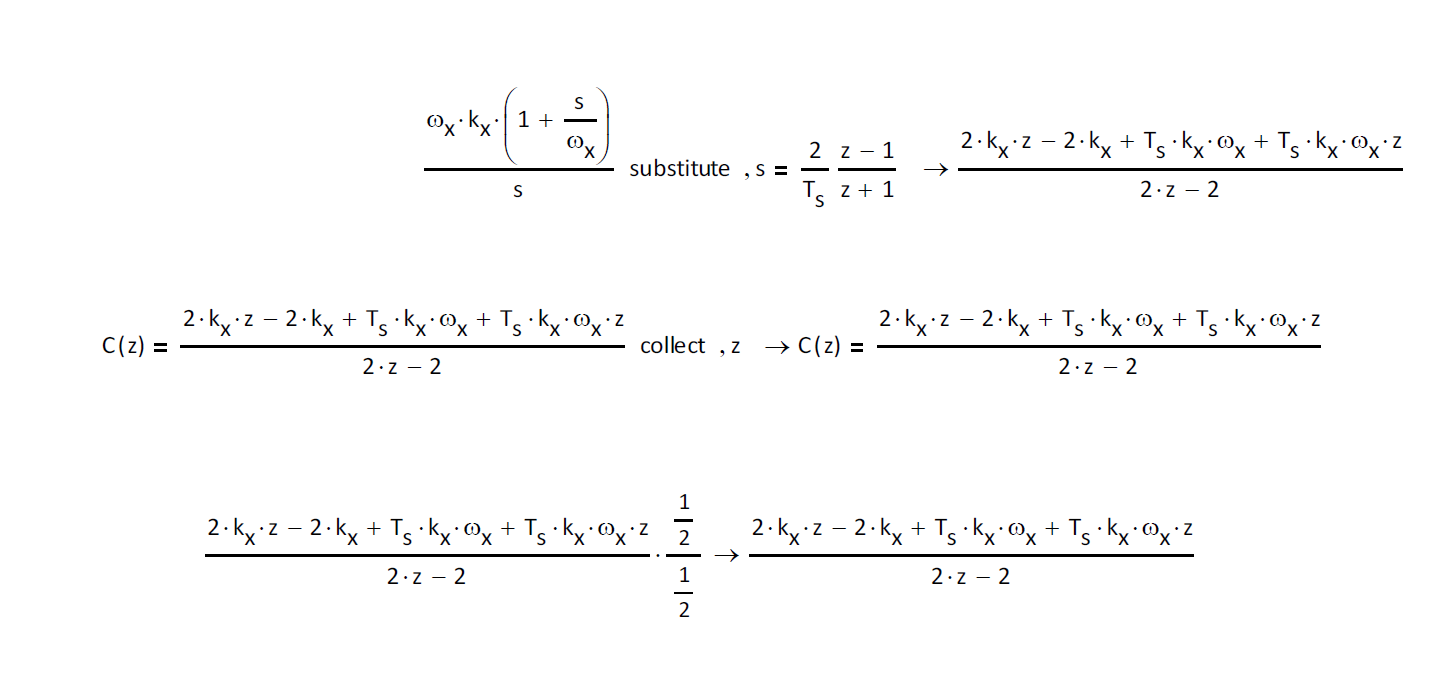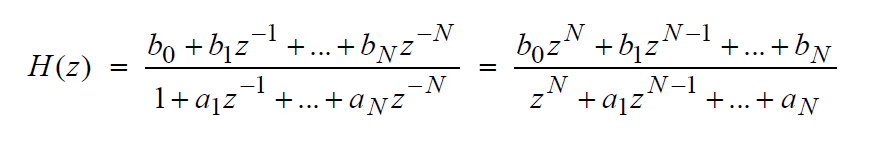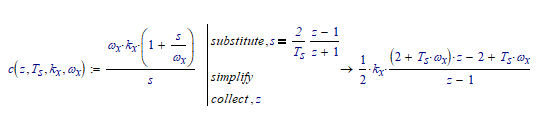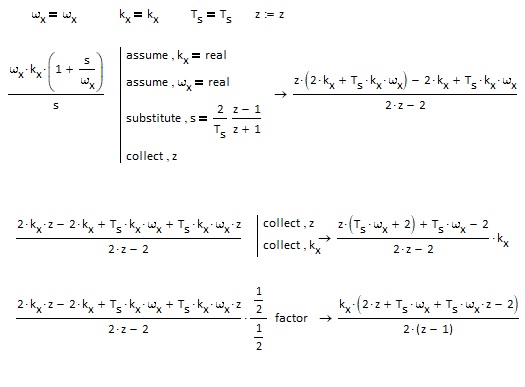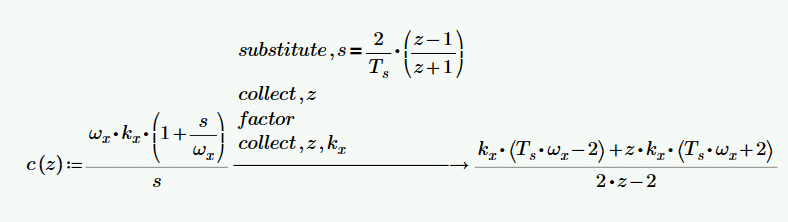Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolics - equation form
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolics - equation form
Hello, I am trying to manipulate some equations into a desired form, specifically in the s domain, into a 'bode' form, and similarly in the z domain.
I am having no success, to the extent that I am struggling in the case of the latter to group terms by the z variable, let alone getting in terms of z^-1. Here's what I am working with at present:
As a first step I'd like to get numerator as a poly in z. A second step is getting into a format of z^-n (n integer), and finally the denominator as (1 - poly in z^-n) also:
Have spent some time trying to manually manipulate the equation to no avail. Any step wise instructions would be greatly appreciated.
Am using v15 (15.0 (M005 [MC15_M005_20101105]))
Example textbook forms of a discrete filter is one of either:
Regards,
Jack
PS have tried to upload my working file but I am gettign the following error: The contents of the attachment doesn't match its file type
PPS have tried to include images of the desired form of eqn and am getting the following error: Message cannot exceed 20,000 characters.
PPPS: Zip File attached in below self-reply.
PPPPS: Images now correctly attached via the menu rather than ctrl-c / ctrl-v
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc.
The other thing I was think might work is define another equation in z with the right number of z terms and somehow getting the two equations to solve e.g. OringinalPoly(z) - NewPoly(z) = 0 solve for coeff. of NewPoly?
Of course I have no idea how to go about that other than the idea...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have an 'equals' (bold 😃 in your expression, which means that the result of c(z)=2*k.x+...etc is either True (1) or False (0), also for the symbolic processor. It also causes it not to collect the z terms.
Better use the definition operator ':' (which shows as ':=') and do like this:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Much thanks all
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Jack,
you can find an extensive discussion of the topic with countless examples built with Mathcad 14-15, by doing a search here:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Much thanks all
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more. . .