Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolics with vectorize & scalar product
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolics with vectorize & scalar product
Hello everyone !
It seems to me that symbolic calculation works strangely when applied to scalar product of two vectors, even if I use vectorize operator.
The consequent error message "Divide by 0" is then not so unexpected... Or maybe it's me who's wrong there.
What's the meaning of the bar above T in one of the symbolic results ? (attached worksheet).
Many thanks, Liv.
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
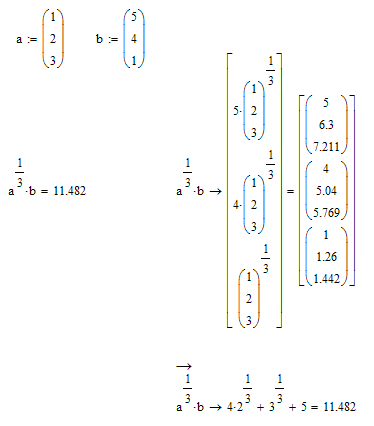
Yes, symbolic evaluation will not use automatic implicit vectorization, whereas numeric evaluation will do.
You have to explicitly vectorize when using symbolic eval (and I would advise to do so with numeric eval as well).
In this case the problem is the exponentiation of the vector, which is not a valid operation on vectors from a mathematical point of view and so muPad refuses to simplify it. In the multiplication the expression is treated like an unknown scalar and thats the reason we get a vector result.
The numerics of Mathcad applies automatic implicit vectorization if an operation is not defined for vectors and does what you probably expected - creating a new vector which then is multiplied by the second vector..
To achieve the same effect using the symbolics, you have to explicitly vectorize that part of the expression.
Example:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

It's because x is undefined. The symbolic solver doesn't mind, simply puts x in the answer.
You use the vectorize operator, so with a vector as input, you should expect a vector as result.
I don't see "the bar above T in one of the symbolic results".
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obviously, you are right there and me definitely wrong ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems to me that symbolic calculation works strangely when applied to scalar product of two vectors, even if I use vectorize operator.
The consequent error message "Divide by 0" is then not so unexpected... Or maybe it's me who's wrong there.
It works, if you vectorize the whole expression (including the division)

What's the meaning of the bar above T in one of the symbolic results ? (attached worksheet).
This means the conjugate complex of T.
It has to do with the mathematical definition of the scalar product:

You can avoid it by using the appropriate matrix multiplication (transpose the first factor to do so)
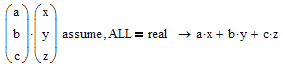
or tell Mathcad/MuPad that you don't use non-real numbers
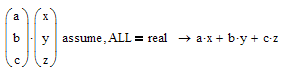
But I am not sure which calculation you had in mind and if that partial vectorization was done on purpose:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think I messed my comments in posted worksheet...
The desired result for Lambda1f is a scalar (a single function of x and T), same as for Lambda2f and Lambda3f. That is a scalar (one function) at both numerator and denominator of Lamda1f.
But you are right, Werner, there is assume/real in Symbolic of Mathcad in order to make use of.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, there's M^1/3 too ![]() , which seems to behave differently in numeric and symbolic calculation...
, which seems to behave differently in numeric and symbolic calculation...

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, symbolic evaluation will not use automatic implicit vectorization, whereas numeric evaluation will do.
You have to explicitly vectorize when using symbolic eval (and I would advise to do so with numeric eval as well).
In this case the problem is the exponentiation of the vector, which is not a valid operation on vectors from a mathematical point of view and so muPad refuses to simplify it. In the multiplication the expression is treated like an unknown scalar and thats the reason we get a vector result.
The numerics of Mathcad applies automatic implicit vectorization if an operation is not defined for vectors and does what you probably expected - creating a new vector which then is multiplied by the second vector..
To achieve the same effect using the symbolics, you have to explicitly vectorize that part of the expression.
Example:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11:
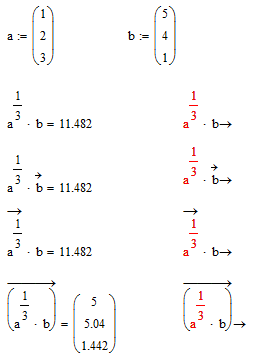
The error messages are in all 4 cases: "No symbolic result was found.", which is a viable statement considering the mathematical incorrectness. But it's sad that the vectorization does not seem to get transferred to the symbolic domain.
Mathcad11/Maple also refuses other exponents (I tried '2').
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guessed that Maple would react differently and I agree that its sad that vectorization does not work as it should with symbolic eval.
Think that has nothing to do with Maple but its a matter of Mathcads interface to the symbolics which obviously was improved somewhere on the way to MC15.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just see that I inserted a wrong picture when I was talking about he matrix product.
It should have been this one
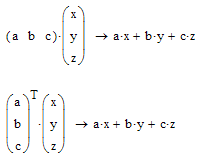
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem solved.
Thank you both, Luc and Werner, for considering it.





