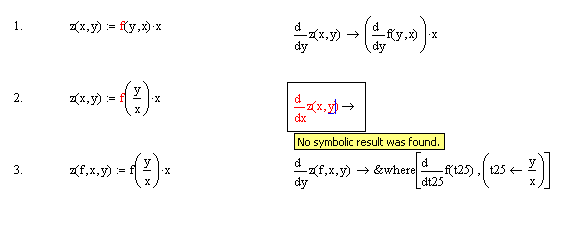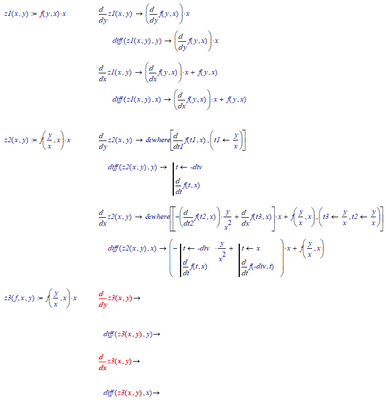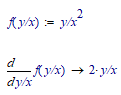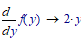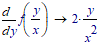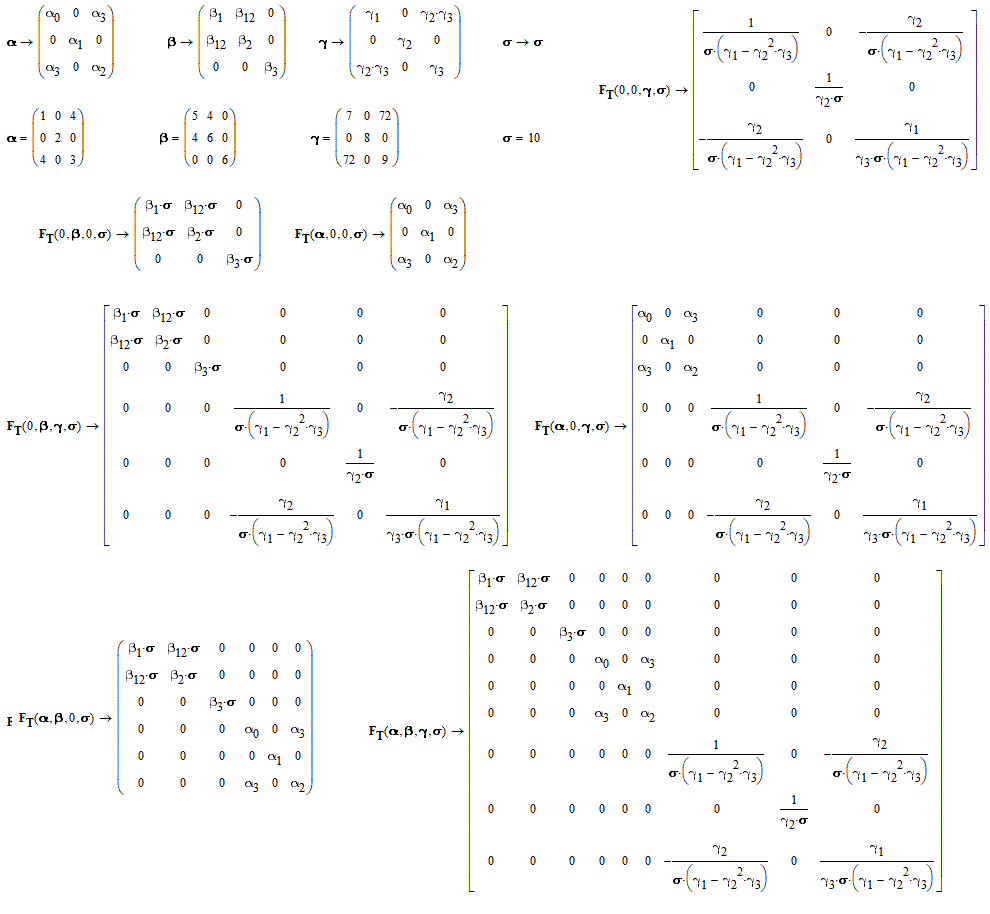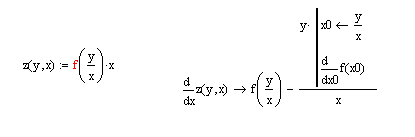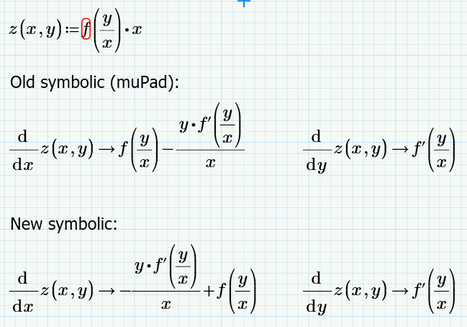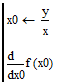Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Symbolics without making explicit a function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Symbolics without making explicit a function
Still using MC 11.2, which (for me) is fine.
I was wonder if a function which is not explicitly expressed, can be used in a symbolic operation. Maple and Mathematica I saw can do it quite well.
Below an example with derivatives.
It seems that only n.1. works while the others (I am in fact interested in a function f(y/x) do not. The n. 3. solution seems incomprehensible to me.
Does exist a trick to make possible to solve for instance function n.2 symbolically?
[[Sol: f(y/x)-[y*f'(y/x)]/x ]]
Thanks.
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Since you're still using Mathcad 11, try using the diff() function symbolically.
It is available due to a backdoor to Maple functionality.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Since you're still using Mathcad 11, try using the diff() function symbolically.
It is available due to a backdoor to Maple functionality.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes Thanks,
apart saying that "diff" does something, I cannot find for equation n.2 [i.e. z=f(x/y)*x] the solution. I don't know even how to interpret "&where" and the various t1, etc.
As I said the solution should be the one I gave in the first post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just a note, in your picture numbers 1 and 3 take derivatives WRT y, but number 2 asks for the derivative WRT x.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>Just a note, in your picture numbers 1 and 3 take derivatives WRT y, but number 2 asks for the derivative WRT x.
Yes, I wanted just to try if there was a difference in processing the symbolic result to derive the variable at the nominator or at the denominator, guessing that the latter was much more difficult to handle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You give the differential equation you are trying to solve as: f(y/x)-[y*f'(y/x)]/x
Assuming the * is meant as multiplication, not as convolution, that is the same as: f(y/x)-(y/x)*f'(y/x)]
And that, after substition t=y/x, is the same as f(t)-t*f'(t). The solution for that DE is f(t)=c*t, or after reverse substition, f(y/x)=c*y/x, where c is to be determined by a constraint.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
you could do as in the photo:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One point, may be helpful to stress that makes my question diverge somewhat from your example. Writing f(y/x) does not necessarily mean that f(x,y):=y/x, but it means that whatever function f is, it is dependent from the compound variable y/x.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I absolutely agree with you. Typically, in Mathcad, when defining a function, the arguments of the function are comma-separated variables and operators are not allowed. However, this is only possible when the function is already defined and a numerical value is desired.
You can see an application of the technique I suggested, in the attached example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"but it means that whatever function f is, it is dependent from the compound variable y/x"
Which in practical terms means: f is dependent on a single variable, also referred to as 'dummy parameter', e.g. t.
It is upon usage of the function that one can decide to supply y/x as the actual parameter, in other terms: that is substitution.
I should think that, also in mathematical terms you cannot define a function f(y/x), unless y/x by itself is identified as a single symbol. As in:
And of course:
but also:
and, not surprisingly:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the further clarification and (MFra) for the file. Congratulations for the latter. Most of it is foreign language for me.
The use of f(y/x) instead of simply f(t) may be explained as follows. In many scientific fields you are interested to both F(x,y) and f(y/x). A simple example. In economics you are interested in both Total Production, but also in Production per Worker. So if you make y=machinery(capital) and x=workers, you could write Total Production using "F", and the production per worker using "f", which is F(y,x)/x=F(y/x,1)--> f(y/x). It is better to keep x separated from y, because you may want to know how production per worker reacts to the change of workers. If you merge x,y into "t", you cannot do that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The use of f(y/x) instead of simply f(t) may be explained as follows. In many scientific fields you are interested to both F(x,y) and f(y/x). A simple example. In economics you are interested in both Total Production, but also in Production per Worker. So if you make y=machinery(capital) and x=workers, you could write Total Production using "F", and the production per worker using "f", which is F(y,x)/x=F(y/x,1)--> f(y/x). It is better to keep x separated from y, because you may want to know how production per worker reacts to the change of workers. If you merge x,y into "t", you cannot do that.
I understand your comment. In Mathcad you define a function with its operators. If you define f(t) using t as a "dummy variable," with or without giving t a value, you can then evaluate f(y/x) for any instance where y and x have defined values--Mathcad will do the division and use that value to replace instances of t in f(t).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Separately you can define the ratio r = y / x and then calculate f (r).. Perhaps it is more understandable the small program, in the attached file, where only symbols are manipulated:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just tried with MC 15 (and curious to know what MCPrime does).
With v.15, at least to me, the result seems much clearer than v. 11.2, and it does not show an error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@anthonyQueen wrote:
(and curious to know what MCPrime does).
You will love it!
One of the few good things in Prime is that they have implemented the prime symbol (f ') as a fully working operator (in MC15 and below it was only available in solve block with odesolve).
So the symbolic results makes use of it and displays like you expected.
In Prime 6 they introduced a new sombolic (friCAS) which is supposed to replace muPad in one of the next releases. From what was posted here in the forum this new symbolic is less capable than muPad (which in turn was much less capable than Maple in mathcad 11).
Nevertheless given your symbolic task even the new symbolic returns the desired result:
Much better than MC15 way to say f ' (y/x) which is
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes @-MFra- @Fred_Kohlhepp many thanks.
@LucMeekes in fact seems right to suggest the use of "diff" function, though in v.11.2 is not listed among "Function..." Insert menu.
Here, it is my understanding: the outcome is less clearer to understand than in v.15, but it works. I hope to have interpreted right.