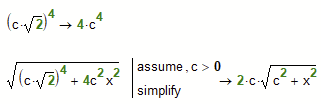Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
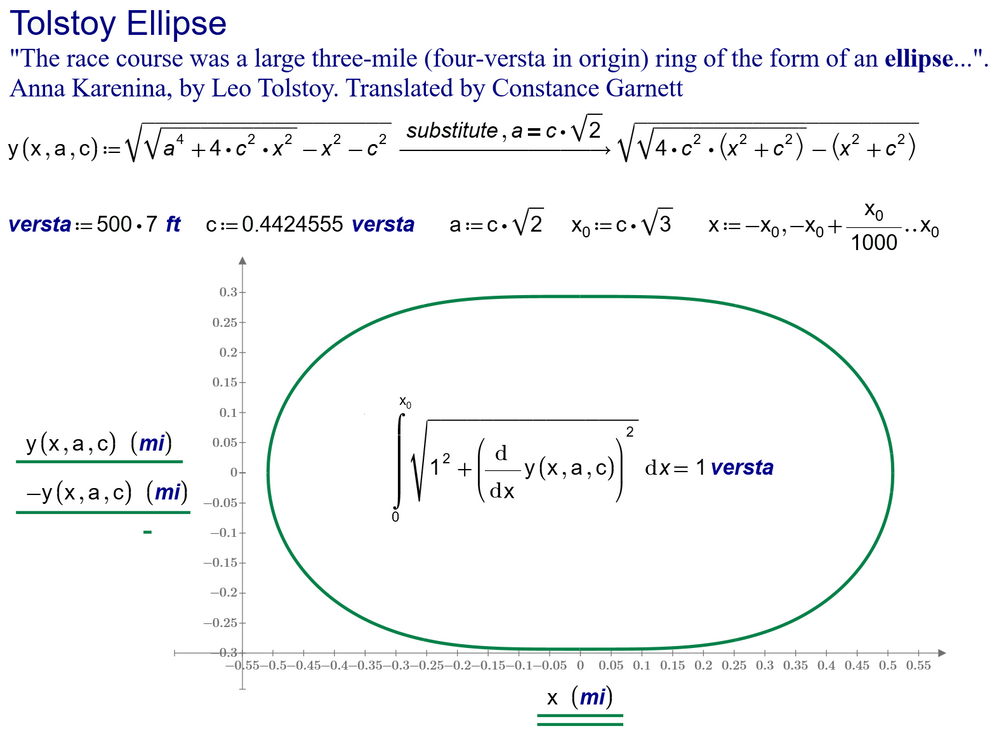
Tolstoy-Ellipse
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Tolstoy-Ellipse
- Labels:
-
Algebra_Geometry
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New math constant?
a/c=1.4142...
c/a=0.70711...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
New math constant?
a/c=1.4142...
c/a=0.70711...
No, not new. Just sqrt(2) 🙂
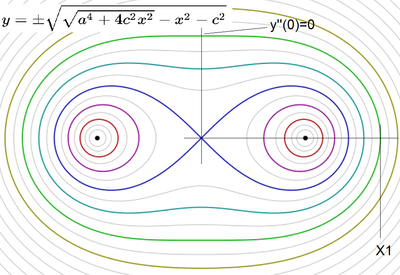
y''(0)=0 is equivalent with a = c* sqrt(2)
You could use this right from the start in your equation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
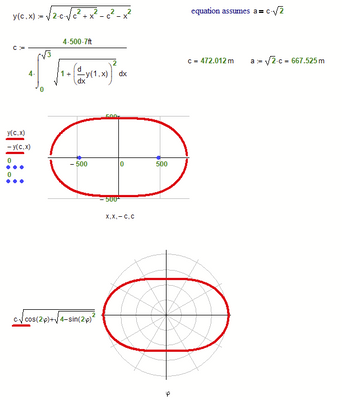
Sorry, the addition of the scaling factor was rather nonsense. Scaling the parameters a and c do the same job, so f is not necessary at all. I guess that getting rid of your variable x1 did the job.
So a shorter solution is this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And here is an even shorter approach which uses, that for the curve you are looking for we have a=c*sqrt(2)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This seems to be so far the shortest solution.
Using no symbolic and no solve block
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
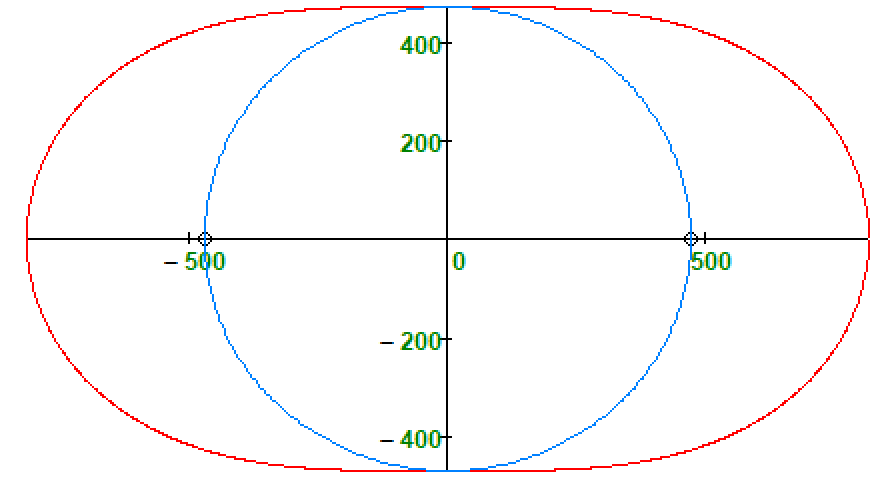
Tolstoy oval
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Tolstoy oval
Yes, I was pretty sure that you still were working on the "Tolstoy oval" you mentioned here https://community.ptc.com/t5/PTC-Mathcad/Leo-Tolstoy-and-Mathcad/m-p/707187#M193887
But now you have to give a concrete mechanical construction method, how one could have drawn this Cassini oval back then. Something similar to the two pegs and the rope with which you can create an ordinary ellipse. I am very curious already 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is such a smart rope - you intercept it into two parts, and the product of the lengths of these parts does not change! a^2!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
There is such a smart rope - you intercept it into two parts, and the product of the lengths of these parts does not change! a^2!
Too bad that the knowledge of this special type of rope has been forgotten over time and they are no longer made these days 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have a little
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator