Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Transportation problem - one paradox
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Transportation problem - one paradox
One Transportation problem
There are two coal mines and two power plants that burn coal. The first mine (m1) gives 50 tons of coal per day, and the second (m2) - 70 tons. The first power (p1) burns 40 tons of coal per day, and the second (p2) - 80 (50 + 70 - 40). Coal is not stored either in the mines or power plants. Costs for transportation of coal are known: 1200 rubles per ton in transportation of coal from the first mine to the first power plant, 1,600 rubles per ton for transportation of coal from the first mine to the second power plant, 800 rubles per ton for transportation of coal from the second mine to first power plant and 1,000 rubles per ton for transportation of coal from the second mine to the second power plant.
The question is how to organize transport (find variables m1p1, m1p2, m2p1 and m2p2), that transport costs are minimal. We can solve this problem in mind, without Mathcad. We have to carry the maximum amount of coal by the cheapest route m2p1 = 40 tons per day. Then m1p1 = 0, m1p2 = 50 tons per day and m2p2 = 30 tons per day. We take these values as a first approximation to the solution of this problem in Mathcad using Given-Minimize.
But look at how Mathcad solved this problem:
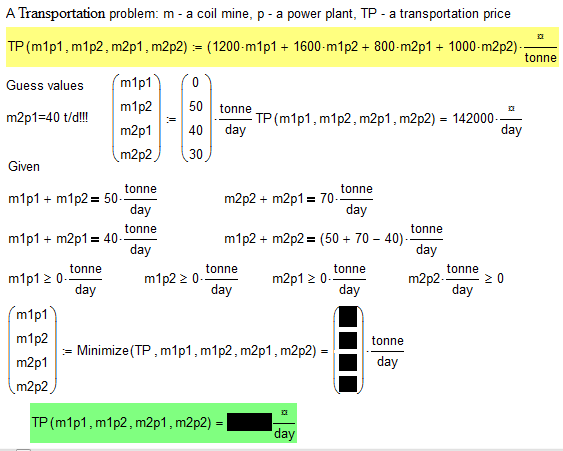
Do you know some others paradox problem - in mind we have one (wrong) solution but in computer we have others (correct) solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, Mathcad Prime cannot solve this problem.
Or I do something wrong?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am confused. Given the constraint, there are 4 equation with 4 unknown. Isn't the four unknown is well defined that way? the four constraint looks linear independent to me at first glance. Therefore there is only one solution and there is no such thing as minimize TP because there is only one solution that can satisfy the four conconstraint.
EDit: the four constraint is linear dependent at second glance. Disregard my message.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator





