Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
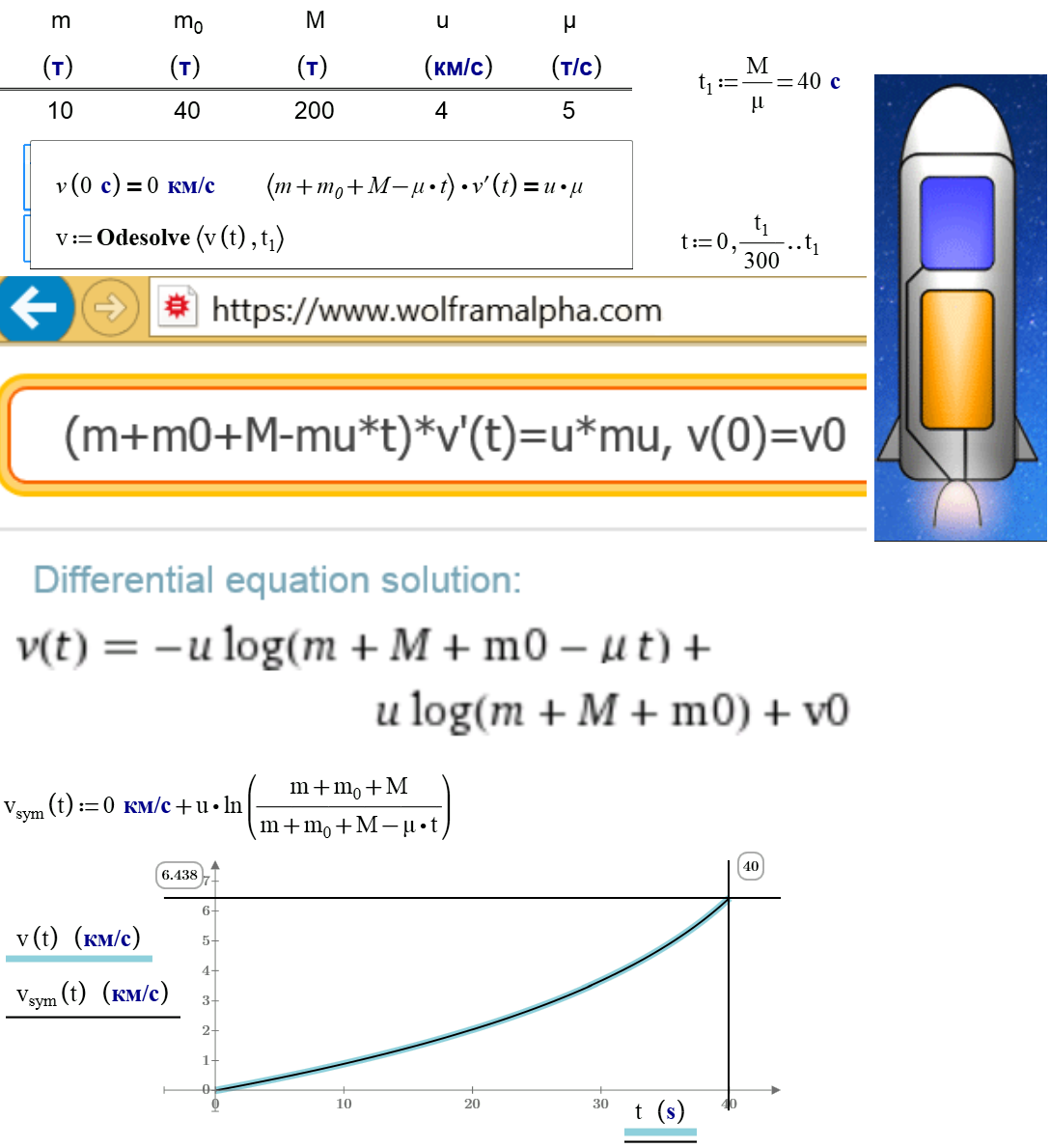
Two stage rocket
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Two stage rocket
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
UK Mathcad Prime Minister is one user of our site about rockets calculation
See please more David Cameron watched Tim Peake's space launch and everyone's laughing at him - Mirror Online

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Valery,
technically the Soyuz is a two-and-a-half (2 1/2) stages rocket as the four boosters start together with the core stage which continues running after the booster have separated. 🙂
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
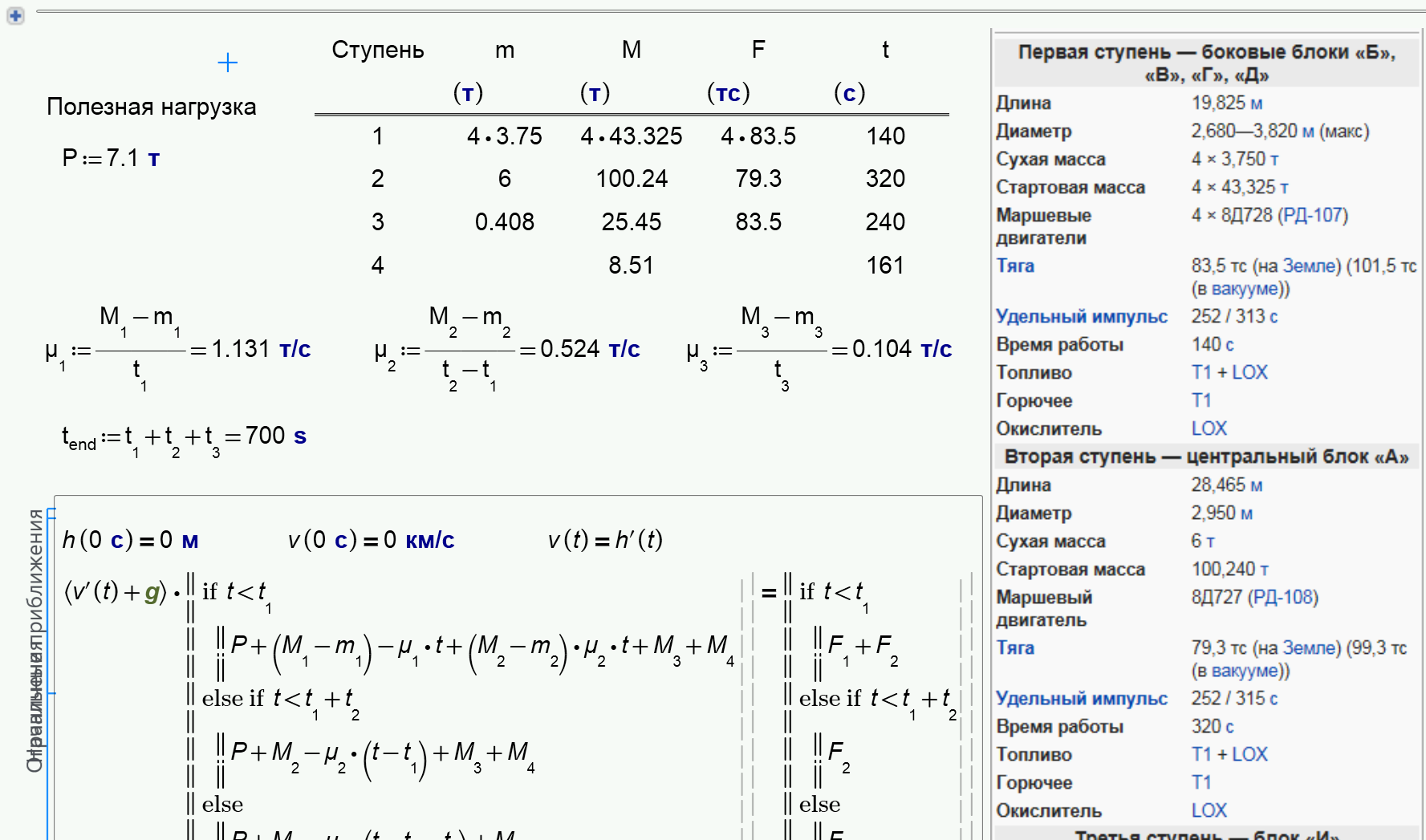
Tanks, Raiko, I Know it. See please - Союз (ракета-носитель) — Википедия
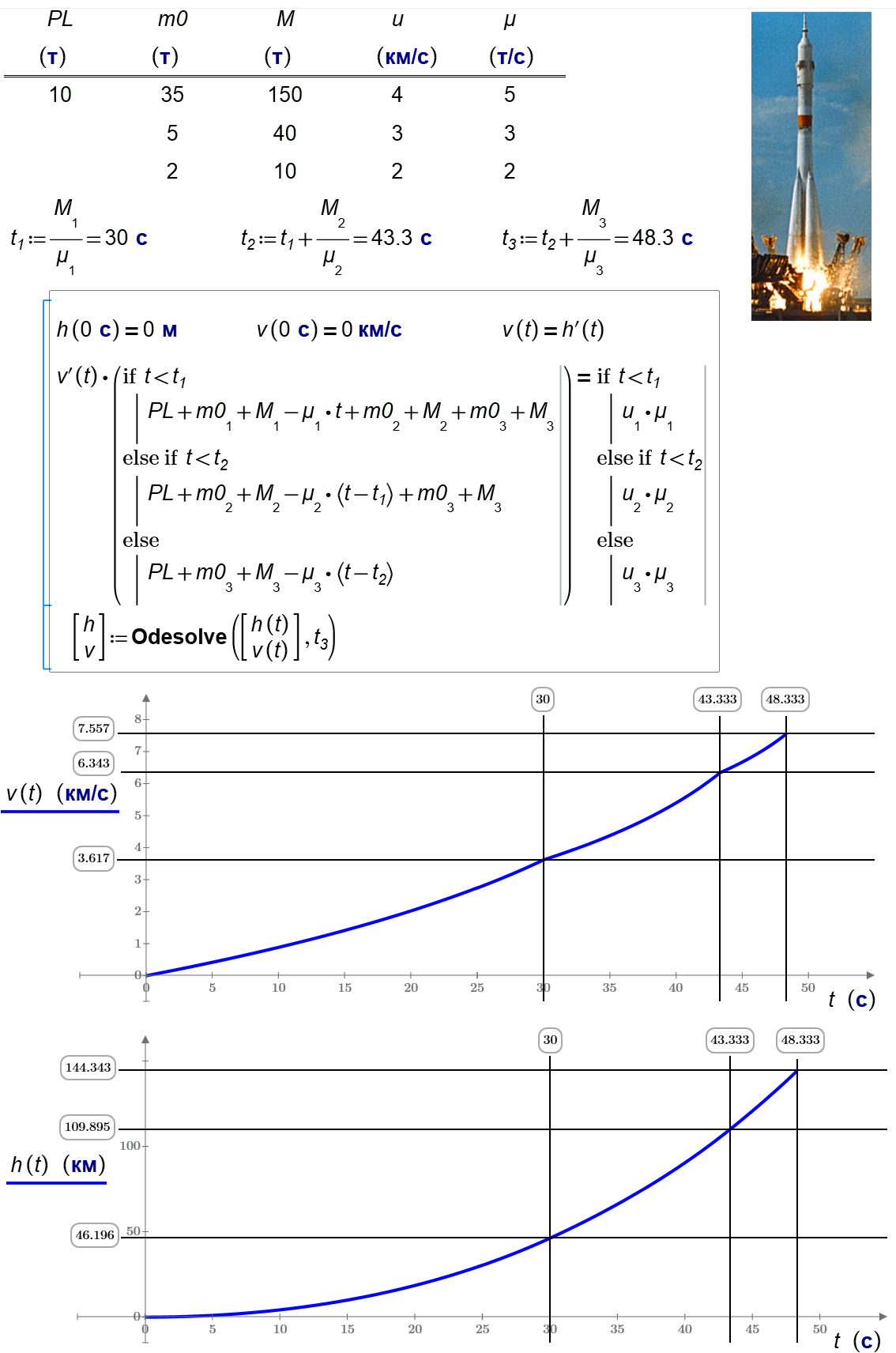
I would like to solve this task with Союз with my students - see Московский лицей 1502. Класс 10-10
Can you help us? With Alvaro and... Isaak!
It is very interesting optimization problem. What is an objective function?!
PS
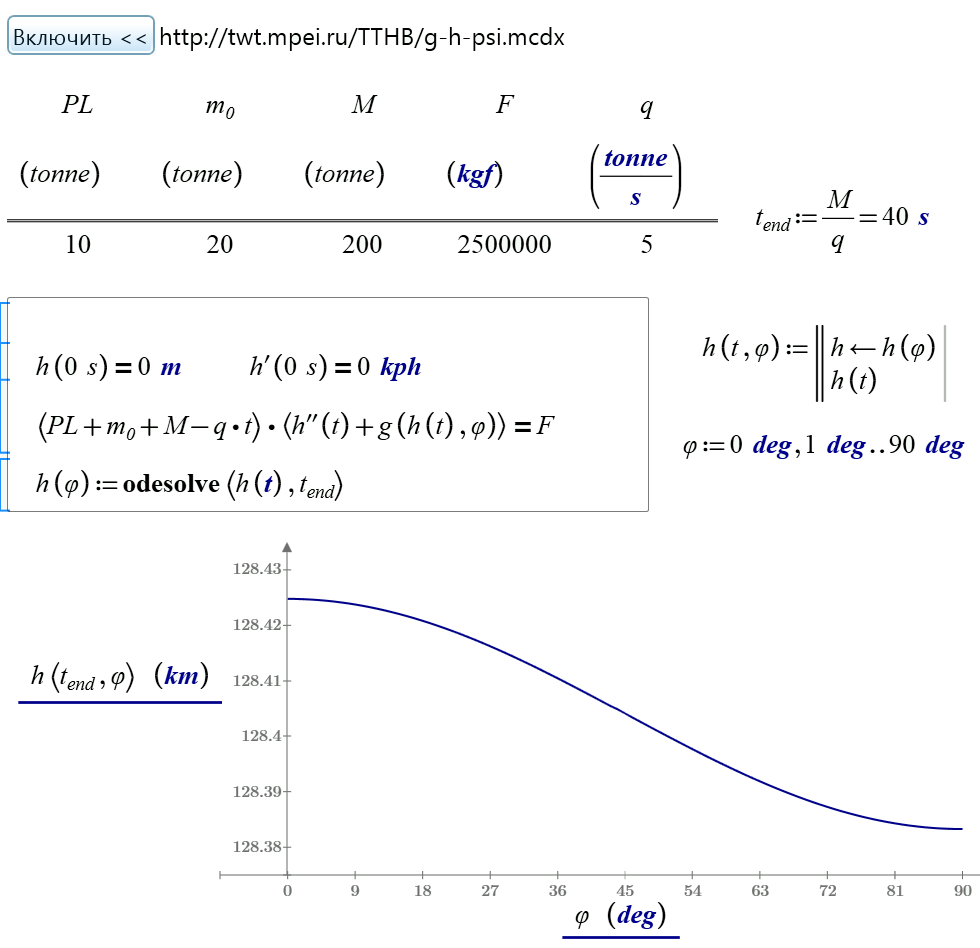
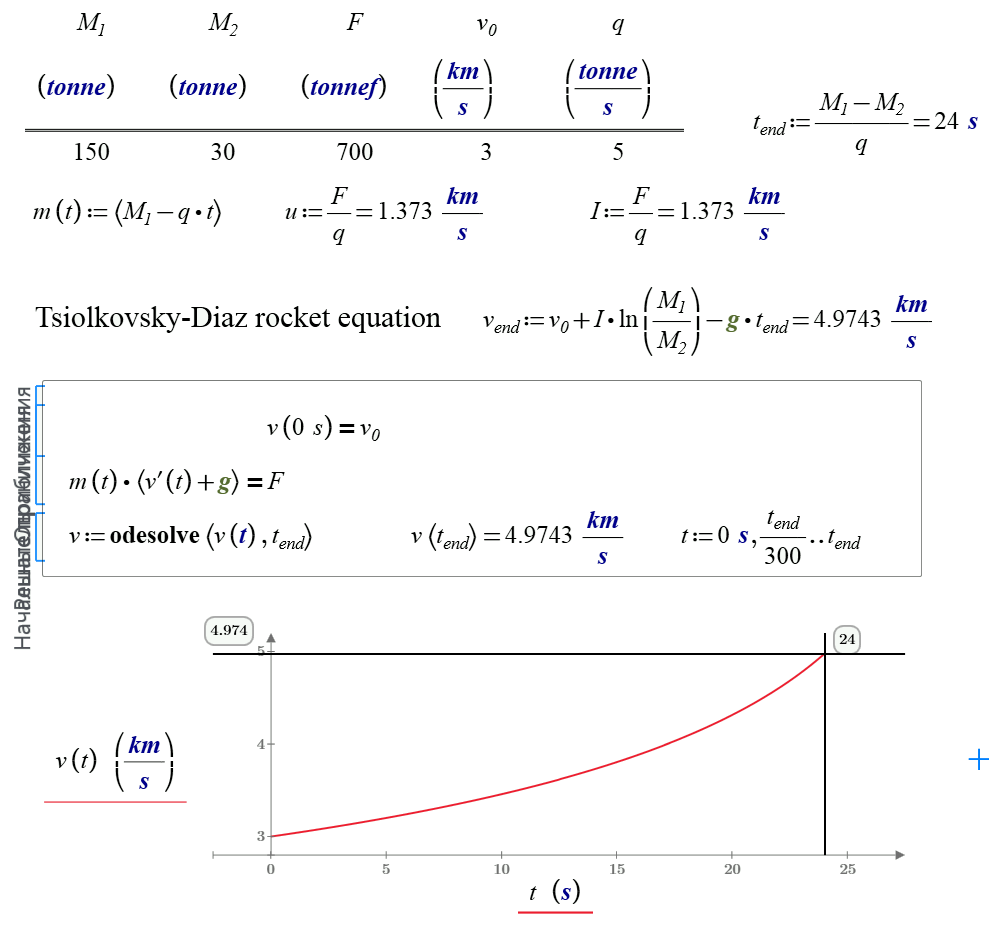
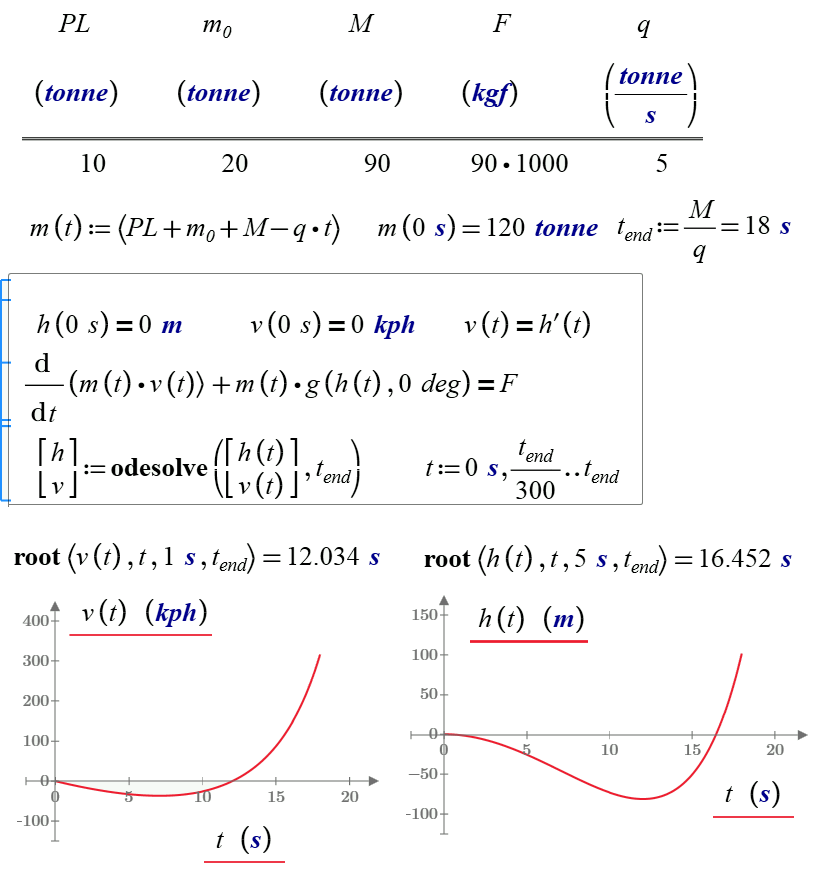
g=g(h(t), altitude)
See please my Mathcad Web-sheet http://twt.mpei.ac.ru/MCS/Worksheets/g-h-psi.xmcd
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Raiko Milanovic wrote:
Hello Valery,
technically the Soyuz is a two-and-a-half (2 1/2) stages rocket as the four boosters start together with the core stage which continues running after the booster have separated. 🙂
Raiko and all
Can you finish the calculation of Soyuz - Mathcad Prime 3.0 shett in attach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry valerij,
but I'm quite busy right now and I would need to install MC prime.
Raiko
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Vallery. Nice example. I guess that what you can remark there is that the equation Force = mass x acceleration isn't true!. Newton equation is Force = dp/dt.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
Hi Vallery. Nice example. I guess that what you can remark there is that the equation Force = mass x acceleration isn't true!. Newton equation is Force = dp/dt.
Thanks, Alvaro.
See please One Rocket (пуск ракеты с подводной лодки)

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alvaro.
But better with units in Prime.
I would like to solve this task 24/10/2015 with my students - see Московский лицей 1502. Класс 10-10
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
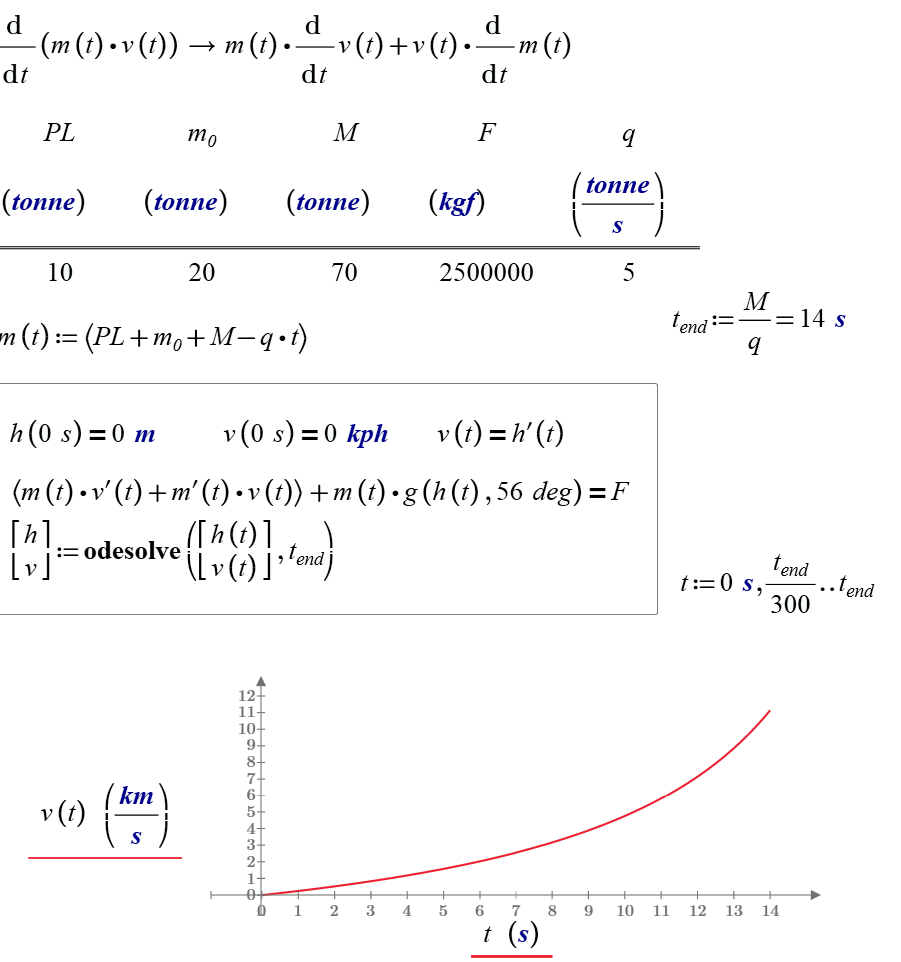
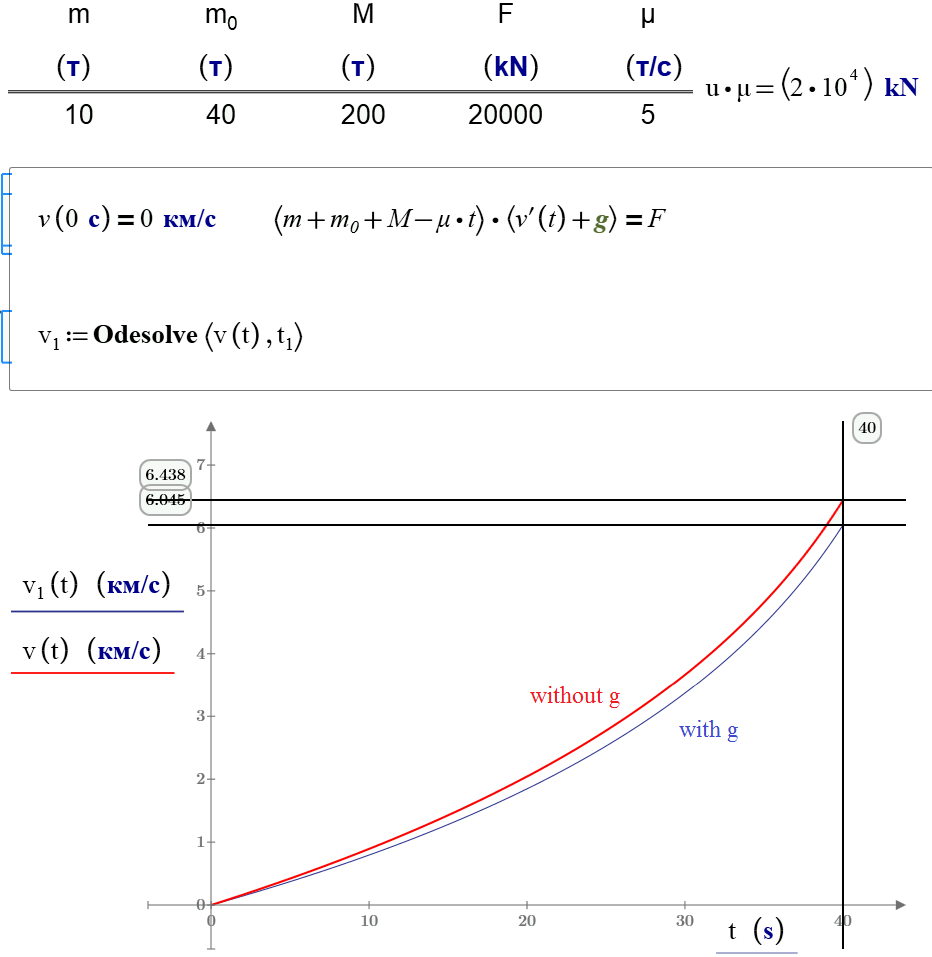
Valery: your ode is mv'+mg=F, true if m constant. But m=m(t) and vary, so you lost the therm m'. The above mc11 ode, and the attached is the same. Newton's law is F=dp/dt.
Best Regards.
PD: Wau! What's an experience work in prime!. I'm need hollidays after this.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, the Newton law is F = m * a
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, the better formulation is the equation (3) m*dv/dt = F + u*dm/dt, in 1992CeMDA..53..227P Page 3:227 . Actually there it is the actual demonstration, using lagrangian mechanics. I guess that you're still loosing the therm in m'.
Best regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No. The introduction of lagrangians don't carry nothing new. The net force go to be the same. See Newton's Second Law of Motion :

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
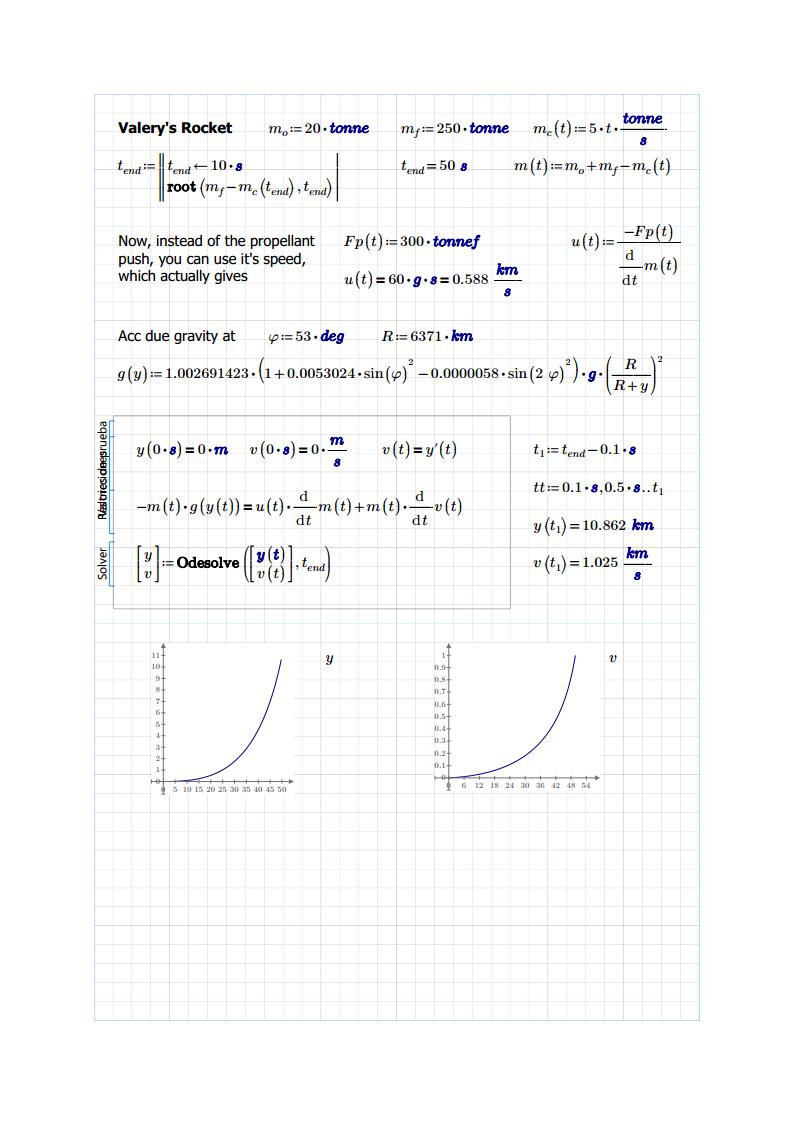
Yes. But analyzing h,v : they are for the "original" rocket, which contains all the fuel. So those values are for the closed system. h is the altitude for the center mass of the expulsed propellant and the "remain" rocket (this is, the rocket with some remain fuel). For determine h,v (in your notation, y,y' in mine) what we need is u = speed of propellant. Whch shows the above paper is the demonstration with the lagrangian of the system that instead v*dm/dt you can use u*dm/dt to get the altitude for the what we call rocket, this is, the remain rocket. This is an open system because it loose mass. And, obviously, u and v have opposite signs. So, you must to provide an additional information u and substitute it's value in the ode. Not very useful, but you can also be interested in the burned fuel, and make the changes in the ode to get it's altitude (accelerating to the earth).
Resuming:
- Closed system, don't loose mass: use F= dp/dpt = m*dv/dt + v*dm/dt.
This is the 2nd Newton's law. h'=v are for the center mass of the expulsed propellant and the remain rocket
- Open system, loose mass: use F = m*dv/dt - u*dm/dt.
where u = vel of the expulsed propellant and h'=v are only for the remain rocket, without the mass of expulsed propellant.
Best regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks,
But why not so:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's ok. What goes 100 meters deep it's the "original" rocket, this is the rocket plus the entire fuel, because what h describe is the center mass height of the all original system. Just like a hand grenade. If before the explosion is describing a parabola, after too, probably not each small piece, but de mass center continues traveling along a parabola. F = dp/dt holds for the closed system, for the open must to correct substituting v by -u.
Kind regards.
Edited: It's almost ok. F is given by v*dm/dt. So, you must to equate to zero the ode. Check my previous attached. There are not a f therm,, therm, but u, speed of the propelant, which gives this "internal" force.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, attached my solutions.
Results agrees with Un cohete de empuje constante (pages uses java, chrome don't support java), but there g=0. About original Valery question, "which's the target" for optimize the rocket, I guess that he want the "perfect" rocket, avaible in the same web: El cohete "perfecto"
Best regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery. As usual, you're right. First solution gives the correct h,v. But, can you deduce from there the kinetics energy, for example? My point is that the relation F = - u*dm/dt gives the correct understanding, and the correct generalization for the Newton law F = dp/dt.
Best regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From my future book:
Dialogue in one teachers room:
The teacher of the Law of God, referring to the teacher of physics: "Today your pet got the deuce. I asked him what it is God's Force (Power). So he told me that it is a product of God's mass on God's acceleration"
Physics teacher: "I told him, and put a deuce in physics. Because the product of God's mass on God's Acceleration gives the Force to the divinity in the square, but not in the first degree."
This old joke has quite serious sequel.
Newton's second law states that the force is the first derivative of momentum (mass times velocity) over time. If the mass is constant (independent of time), it can be taken out from under the sign of the derivative, and then the Force will be equal to the product of mass and acceleration - the first derivative of the velocity with respect to time.
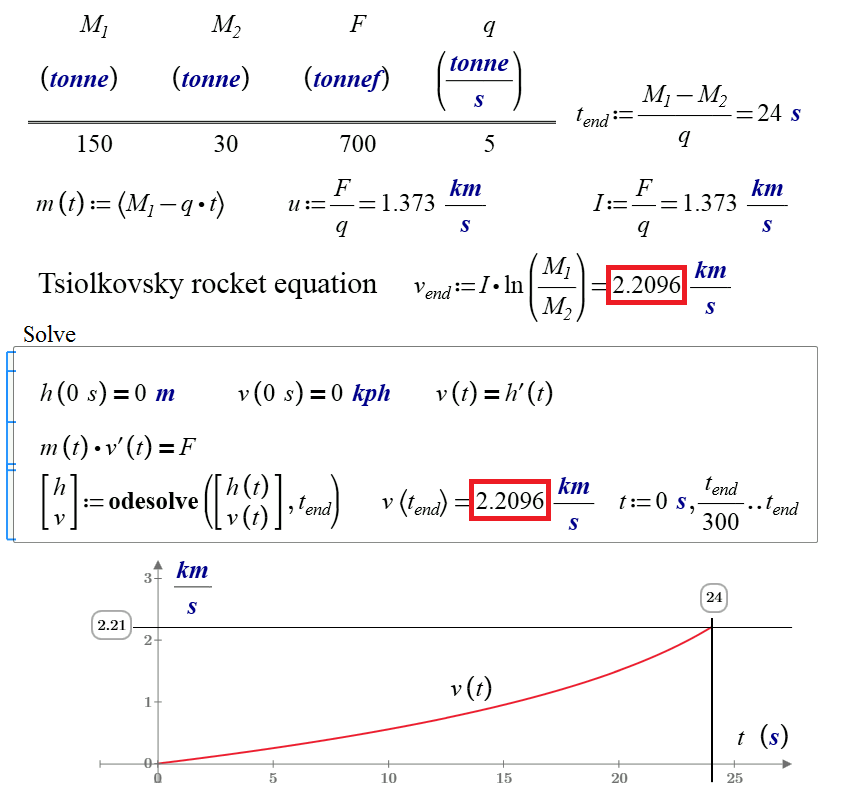
But there are cases when the mass is not constant. Solution of this problem is shown in Fig. 9.37: missile has a launch mass of 270 tonnes, of which 250 tons - a fuel and an oxidant are consumed at a rate of 5 tons per second. Thrust rocket engine - 300 tons of force. The question is, what is the missiles final velocity?
And more
In this task, the mass of the object (material point) the value of the variable. Which edition to use in this problem Newton's second law? Here we must recall the inertial and non-inertial reference systems, not only Newton, but also about the Lagrangian and Hamiltonian...
Currently, almost all physics journals not to consider not only the articles describing perpetual motion, but also articles describing applications of Newtonian mechanics. But this book is not about the mechanics and how the old "bearded" The problem is solved with the help of modern computer programs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hope an other excellent book by you, Valery. Just a few comments this equation: F=dp/dt It is used for relativistic's with p = (m0*lambda)*v, where lambda is the "contraction factor", 1/sqrt(1-v^2/c^2), given a system with variable mass. And all people happy, even it's well know that this is only for the "special" theory, where subsists some kind of intuition, because there are some special inertial system of reference. But all of this theory is wrong: maybe the general theory is true, but for sure not the special. Same thing happen with the Maxwell equations of the electromagnetic theory: all are wrong. Not just that: they are inconsistent. But we go still to use those wrong equations for a long time, taking care not to force them. Well, Newton's laws are all wrong. And inconsistent. So, if F=dp/dt don't follow some Galileo's invariant, can't be a surprise. A lot of sources, including Wikipedia, prevent for not use it because Newton's 2nd law, even he enunciate it not as F=m*a, but as F=dp/dt, are true only for constant mass systems. Well (again): actually they are never true. Badly: are inconsistent. But people insist in using it. Maybe because can found useful results. So, if F=dp/dt is good for special theory of relativity, I want to show that is good for non-relativistic rockets too. And, even I never read the orginal (this is, the Principia Newton's book) I guess that for some reason he stablish that F=dp/dt, despite if m is varying or not.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the Soviet cult film "Nine Days of One Year" two characters debate about space flight. One character makes calculations in Mathcad, sorry, on a napkin.

I tried to reconstruct these calculations with Mathcad (sorry - without the Einstein theory):

View the film: Девять дней одного года (1961) смотреть онлайн бесплатно
A little about the movie:
The film is about a young nuclear scientists in the 60s. Gusev and Kulikov put important experiment, it is possible, but one of the physicists subjected to radiation. He did not tell anyone about what happened, it is closed with his wife and friends who do not understand his change, if not feel puffed up madcap.
Teammate Kulikova, learns the secret of another, and insists on the operation of a bone marrow transplant to save lives.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the film between the characters (and Evstigneev and Kazakov) takes such a dialogue:
- Tell me, Valery Ivanovich, how deep you're going to get into the depths of our galaxy?
- At 500 light years.
- How fast?
- Close to the speed of light.
- Weight of the ship?
- One hundred thousand tons.
- Fuel?
- The most modern.
- We calculate how much fuel you need. Kindly napkin
..
Nikolai Ivanovich, you have completed your calculations?
- Yes please. Weighing spacecraft hundred thousand tons at a speed close to the speed of light, for the overflight of the Galaxy within a reasonable period of human life you need ten to the twenty-second degree tons of modern fuel. Reference. Our planet weighs slightly less. Happy journey!
777 for Happy journey too!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have a small mental experiment for your book. Think about a small perfect spherical of matter traveling by the empty with constant speed. Seems to be a very bored experiment. But, surprise: the material of the sphere was radioactive. Now loosing mass implies to loose some few kinetic energy and as all engineers well knows, with the energy, food and radioactivity, do not play.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I told this to my friend Isaac,,, (Albert is back)

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Valery,
I have problems replicating your first equation in Mathcad 15. I got rid of the units by using UnitsOf(xyz) but still it doesn't compute. any advice what I'm doing wrong apart from not working enough with ODEs?
Raiko
Sorry, I forgot to add the sheet