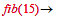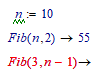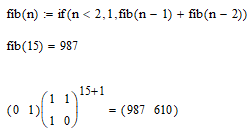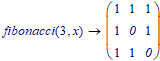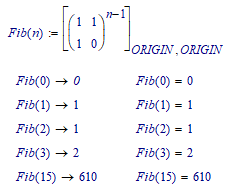Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Undocumented function fibonacci
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Undocumented function fibonacci
Can anybody explain what the function fibonacci (undocumented, symbolic only, Mathcad 11) does?
It accepts more than one argument, but only the first appears to be observed.
Luc
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Good catch! but missed one:
Solved with:
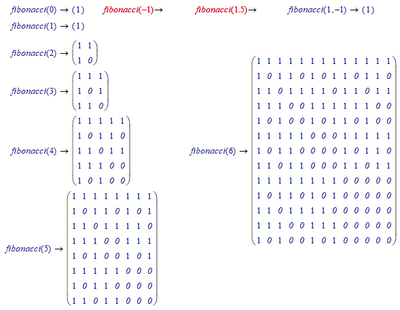
Unfortunately matrices get (too) big:
(No symbolic result was found).
Further, returning to:
In other words,
Fib(n,2) = Fib(3,n-1) gives the n'th term of the fibonacci series.
Fib(n,2) is the better choice, because it keeps the matrix small:
The other series can be searched in the Online Encyclopedia of Integer Sequences:
1,1,3,7,17,41,99,239 is Numerators of continued fraction convergents to sqrt(2).
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks to me that the Maple help here
https://www.maplesoft.com/support/help/maple/view.aspx?path=combinat%2Ffibonacci
explains it. What MC11 shows may have to do with the matrix A^n binary powered mentioned in the help even though I don't see why and how the matrix should grow that way - an intermediate result of the binary exponentiation, not supposed to bubble up to the surface?
It looks like the number of rows (and columns) of the matrices you show correspond to the fibonacci numbers.
Whats the result of fibonacci (3,x)-> ?
Needless to say that fibonacci(,,) is not present in MC15 or Prime which use different symbolic engines,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is:
As indicated, the function allows many parameters, but only observes the first:
I think you have an error in your fib() function, fib(0) should be 0, not 1. According to the definition (?) the sequence is:
0,1,1,2,3,5,8,13,21,34,55 (see your link).
I get to fibonacci numbers with a simpler expression:
But now I can replace the 2x2 matrix with fibonacci(m) and introduce a second parameter, which for m=2 gives the 'normal' fibonacci numbers:
(For m < 2, the result is always 1 for any integer number n),
As stated above, m must be integer (too), so it seems not related to the x in the Maple article.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
According my fib function - I simply was to lazy to nest another if-function 😉
With the undocumented function fib(n):=rows(fibonacci(n))*(n>0) should do the job, too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Good catch! but missed one:
Solved with:
Unfortunately matrices get (too) big:
(No symbolic result was found).
Further, returning to:
In other words,
Fib(n,2) = Fib(3,n-1) gives the n'th term of the fibonacci series.
Fib(n,2) is the better choice, because it keeps the matrix small:
The other series can be searched in the Online Encyclopedia of Integer Sequences:
1,1,3,7,17,41,99,239 is Numerators of continued fraction convergents to sqrt(2).
Luc