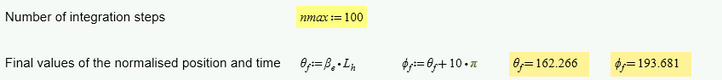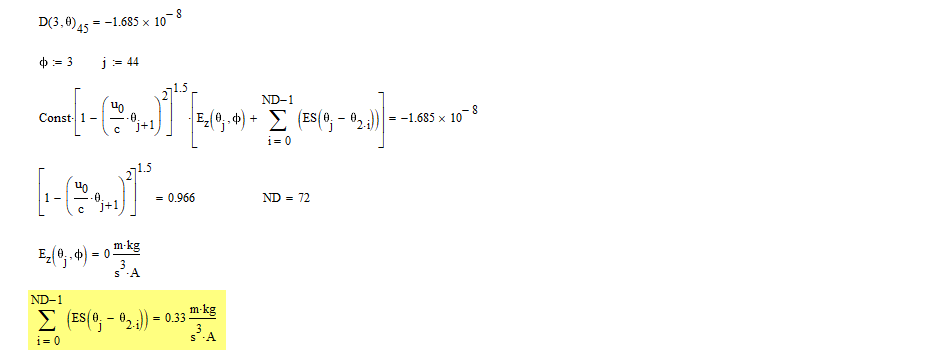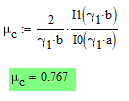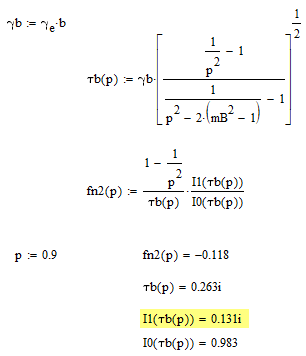Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Units are not compatible in ODE solver
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Units are not compatible in ODE solver
Hello,
I have a worksheet created with Mathcad 15 and was recently converted to Prime 8.0. After the conversion, I got this error message saying "units are not compatible" in an ODE solver as shown below:
The initial and final conditions were defined as
This problem did not occur in Mathcad 15 and before, and I have been struggling for days to solve this.
Does anyone have any suggestion?
Thank you!
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, I looked at the index 45 and calculated it outside the function in MC15 and Prime.
The main difference occurred in the sum calculation
So I looked at the individual summands but could not spot a significant difference with the naked eye. Therefore I exported the MC15 result and imported them in Prime.
As you can see, the two vectors actually sum up to about the same value bt with different sign. But largest difference of the two vectors is just +/- 1.9 at values in the range of 10^4. Thats not much of a difference, but on the other hand the sum of the vector also is just +/- 0.3. This means that the large positive and the large negative values in this vector cancel and small differences may push the result on the positive or negative side.
I would also guess that these differences are not the cause for AdamsBDF failing (but then - who knows?).
I have to leave it up to you to further investigate in the (only small) differences in the two vectors, find out where they may stem from and if they could be responsible for the ODE-solvers failing ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
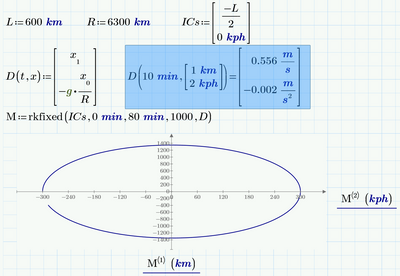
Check please what values returns the D function!
One example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess the sheet doesn't use any units, right?
Its hard to debug just a picture so if possible you should attach the sheets (Prime and real Mathcad).
We don't see where and how "c" is defined in your sheet.
My best guess is that the "c" in your definition of the function D is labelled as "constant" and so is interpreted as speed of light.
Try to relabel "c" in the definition of D(...) as "Variable" and see if it helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks for the prompt response!
The sheet does use units, but both "phi" and "theta" are unitless for D.
Changing "c" to a variable doesn't seem to solve the issue.
I am attaching the worksheet (Prime and Mathcad 15) here. As you can see, "Z" was computed correctly in Mathcad15.
I would really appreciate it if you can help me look into it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, I see that c actually is supposed to be the predefined constant for speed of light and its units cancel with those of u.0.
So of course c should not be labeled as Variable.
Also the units of E.z and ES cancel with those of "Const", so D is actually unitless.
I also can confirm that the MC15 sheet is working OK.
At the moment I can't see whats the cause for the sheet failing in Prime and which units it thinks are not compatible .
Numerical algorithms have been changed when going from MC to Prime, so my vague guess is that this could be the cause of the problem.
One additional observation:
When I try to evaluate the function D( ) with an arbitrary (unitless) value for the first and the predefined vector for the second argument, I get the very same unit mismatch error, but this time we can trace it back to the sum in the definition of D ().
Nonetheless I could not find anything wrong here ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
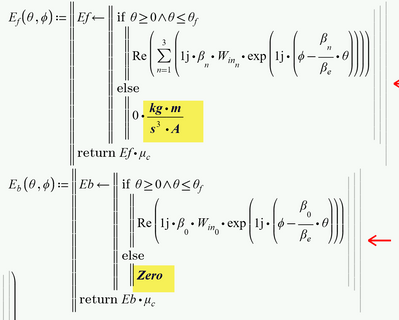
Guess I got (EDIT: only partially 😞 ), was a bit tricky!
Problem was the function E.z which is defined using E.f and E.b. It sometimes (j=0) returns a zero without any units!
Prime, unlike MC15, does not use SUC (static unit check) and so you must provide a correct unit even though the value is zero. As an alternative you may use the predined constant "Zero" (note the capital "Z", there also is a predefined constant "zero" which doesn't do the job).
So you have to change these two functions:
EDIT: OK, but now the next problem:
????? no clue, sorry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you! This is very helpful!
Let me double check the function array in D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Shasha wrote:
Thank you! This is very helpful!
Let me double check the function array in D.
Yes, that would normally had been my suggestion but what irritates me is that I had seen it working OK in MC15 ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are 143+1 equations and 143+1 rows returned from D, I honestly don't see the difference. However, if I plugin specific phi and theta for D, there are discrepancies between the results from Prime8 and Mathcad15:
Prime 8: Mathcad15:

The sign of D(...) should be negative until reaching to row 73. Not sure why this happened, but I will check the previous calculation.
Thank you so much for helping me look into the issue!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, I looked at the index 45 and calculated it outside the function in MC15 and Prime.
The main difference occurred in the sum calculation
So I looked at the individual summands but could not spot a significant difference with the naked eye. Therefore I exported the MC15 result and imported them in Prime.
As you can see, the two vectors actually sum up to about the same value bt with different sign. But largest difference of the two vectors is just +/- 1.9 at values in the range of 10^4. Thats not much of a difference, but on the other hand the sum of the vector also is just +/- 0.3. This means that the large positive and the large negative values in this vector cancel and small differences may push the result on the positive or negative side.
I would also guess that these differences are not the cause for AdamsBDF failing (but then - who knows?).
I have to leave it up to you to further investigate in the (only small) differences in the two vectors, find out where they may stem from and if they could be responsible for the ODE-solvers failing ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot for helping me digging into this!
I also doubt these differences are the cause of the ODE solver not working, but I will keep looking.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just an update, I figured out the issue with the ODE solver. The problem was one of the variables that was calculated at the beginning.
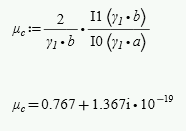
The result of this calculation had a very small imaginary part. which did not appear in Mathcad15.
I took the real part and it eventually solved the ODE issue.
Thanks again for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OMG, thats really tricky!
Actually the problem is already here the calculation of omega.q
If you change the guess value p0 to something in the range 0.2 to 0.8, the result is pure real.
In MC15 you run into the same problem if you set the guess as high as 0.98.
So its already this position where you should use the Re() function or taking the absolute value.
Further investigations show that the actual difference seems to be in the result of the Bessel function I1. In Prime we see a very tiny real part (!) which seems to be responsible for the non-real result of fn2 and fn.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I have noticed the omega_q also has a small imaginary part. However, it does not affect the solver since it's not in the ODE equation.
It's great to find out the initial guess value of the Bessel functions played major part in this calculation.
Again, really appreciate your diagnostics!