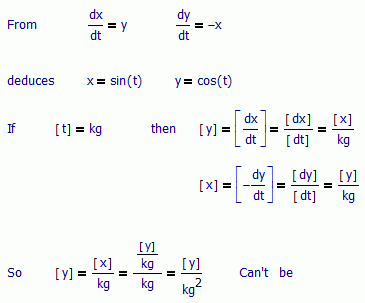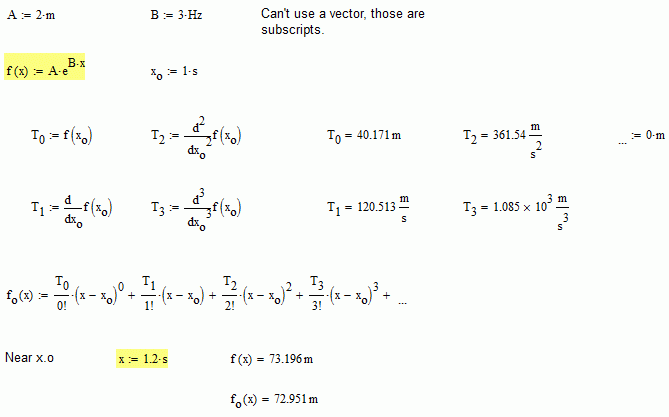Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Units in roman
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Units in roman
Units in roman
I challenge anyone to find a scientific paper or a book in any science or engineering discipline, published by a reputable company, in which units are shown in italics. Please let me know if you find one! In state-of-the-art publishing, units are printed in roman (upright and not bold).
“The International System of Units”, now adopted throughout the world, specifies which units to use and how to write them. Defined in the SI Brochure , it is clear on the subject:
Chapter 5: Writing unit symbols and names, and expressing the values of quantities
Unit symbols
Unit symbols are printed in roman (upright) type regardless of the type used in the surrounding text. They are printed in lower-case letters unless they are derived from a proper name, in which case the first letter is a capital letter.
The National Institute of Standards and Technology (NIST), an agency of the U.S. Department of Commerce, has published “The NIST Guide for the use of the International System of Units”, which is also clear on the subject:
Chapter 6. Rules and Style Conventions for Printing and Using Units
6.1.1 Typeface
Unit symbols are printed in roman (upright) type regardless of the type used in the surrounding text. (See also Sec. 10.2 and Secs. 10.2.1 to 10.2.4.)
where Sections 10.2 and 10.2.1 to 10.2.4 restate and explain the rule.
Essentially, units are written in roman in order to distinguish them from variables which are written in italics. For example, "m" is a variable whereas "m" is a unit. Please refer to one of the above publications for more details. Note that the color of the font for units (as well as for numbers, variables, etc.) is not addressed in these documents..
In Mathcad, displaying units in a color different than that of variables is a good way to distinguish them even better. However, displaying them in italics is unnecessary and wrong.
Mathcad default setting
All the marketing for PTC Mathcad is done with the units shown in bold blue jazzy italics and the product is delivered with this font set by default.
When asked why the default font for units is such, PTC Mathcad dodges the question by saying that, in Mathcad, names of units are treated as variables, so if variables are in italics so should be the units, and that anyways users can easily change the font for units.
The problem
The problem is that my students, who use Mathcad, could think that the default font for units is correct, whereas actually it is wrong and unacceptable.
I have to ask my students to change the font to roman. If they ask me, I can only explain to them that the funny default font was probably a request from the company’s marketing department.
Correcting the situation
There are laws behind the recommended use of the SI units in the U.S. and other countries around the world. Standards are intended to ensure public safety and to improve efficiency in commerce, heath system and teaching. Non-compliance can result in large economic losses. Students are entitled to be taught properly. A court could consider that PTC Mathcad has mislead its users, thousands of students and companies, in thinking that the proper font for units is italics.
While a lawsuit against PTC Mathcad is unlikely, but possible, the company should set a good example and correct the situation by doing the following:
- Clarify the distinction between fonts for units and for variables.
- Change the factory default setting of the font for units to roman (upright and not bold). Colors are fine.
- Modify all advertising to show units in the way described above.
- Publish a white paper announcing the change and saying how great the company is for complying with state-of-the-art publishing and the worldwide SI standard.
References
The “SI Brochure” is available in English at http://www.bipm.org/en/publications/si-brochure/.
“The NIST Guide for the use of the International System of Units” is available at http://www.nist.gov/pml/pubs/sp811/.
Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
But for make this conventions, at least, there are some considerations, for example, can ask for some coherence. If sin(2 kg) have sense, in the functional definition for sin, you have this:
The problem with your argument is that [y] is not (generally) equal to [x]/kg. Let's revert to the standard [t] = s, [x]=m, [y]=m, dx/dt = y is equivalent to {dx}[x]/{dt}[t] = {y}[y] == {dx}/{dt} m/s = {y} m. Clearly there is a problem here, as whilst no one is going to argue with the numerical value equivalence, metres-per-second is not equal to metres dimensionally.
This highlights one of the major problems with creating a system of quantities that includes extra dimensions, and is effectively the same problem we have with many legacy formulae - there is a hidden (very assumed) conversion factor needed to dimensionally balance the equations.
In this case, keeping it simple by letting [y] = [x] = m, the dimensional form of the equation should be (assuming that speed is the desired quantity😞
dx/dt = k•y
= {dx}/{dt} m/s = {k}[k]•{y}m, where {k} = 1
reducing dimensionally to
= m/s = [k] m
which gives
[k] = 1/s
Replacing [t] with kilograms rather than seconds trivially gives the [k] = 1/kg
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
a few reference to various arguments about such computations..
units - Fundamental question about dimensional analysis - Physics Stack Exchange (don't forget the right hand side Linked and Related potential light reading..)
http://www.chem.utoronto.ca/~cmatta/2011_JChemEdu_Dimensions_and_Logs_Matta_Massa_Gubskaya_Knoll.pdf paper on "Can One Take the Logarithm or the Sine of a Dimensioned Quantity or a Unit? Dimensional Analysis Involving Transcendental Functions" by Cherif F. Matta (linked in one of the comments regarding 'paywall') Interestingly he's interested in the empirical chemistry equations!
logarithms - Units of a log of a physical quantity - Mathematics Stack Exchange (a mathematicians view..) has links to the above.
The Matta paper then links to the paper I previously mentioned http://web.ist.utl.pt/ist12219/data/60.pdf
"Two alternative derivations of Bridgman’s theorem":
Abstract '
One of the fundamental results of Dimensional Analysis is the so-called Bridgman’s
theorem. This theorem states that the only functions that may have dimensional arguments
are products of powers of the base quantities of a given system of units. In this work,
Bridgman’s theorem is discussed and rederived in two different ways, one not involving
calculus, and a second one based on a Taylor series expansion analysis.'
Some nice bed-time reading.
--
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Philip Oakley wrote:
The Matta paper then links to the paper I previously mentioned http://web.ist.utl.pt/ist12219/data/60.pdf
"Two alternative derivations of Bridgman’s theorem":
Abstract '
One of the fundamental results of Dimensional Analysis is the so-called Bridgman’s
theorem. This theorem states that the only functions that may have dimensional arguments
are products of powers of the base quantities of a given system of units. In this work,
Bridgman’s theorem is discussed and rederived in two different ways, one not involving
calculus, and a second one based on a Taylor series expansion analysis.'
I've had a very quick scan of that paper. As it's just a skim, and informed by your text, am I correct in believing that the (confirmed) theorem is that any function f(x) can only have dimension other than 1 if f(x) has the form αxβ (eg, 3•x2 for x = 2 m gives 12 m2)?
Edited to Add:
So a function like f(x):= 2•x2 + 3•x3 would be forbidden because it would try to add m2 to m3?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Essentially yes.
However the taylor expansion part can be used to show that, when viewed as trigonometry, the sin/cos/tan of angles reguires an angle dimension depending on how you view it.
The paper even covers that just because A=2kg, it doesn't mean that ln(A)=ln(2kg) is valid (i.e. it is not valid physically); while A=2 would allow ln(A)=ln(2) which is valid as it's just pure maths.
The footnote on page 2 is neat as well. There's more on hsm.stackexchange.com on when the different points in history where (i.e. what predates what).
It's also interesting to look at how they did (trig) angle calculations 'back in the day' (when a nautical mile was a minute of arc, and the French were defining the meter as a metric second (of arc), and angles were rational fractions of a right angle, etc.) When was the term radian first coined?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Philip Oakley wrote:
StuartBruff wrote:
So a function like f(x):= 2•x2 + 3•x3 would be forbidden because it would try to add m2 to m3?
Essentially yes.
OK. Then I believe it's wrong. One of the very first equations I was taught in physics was the famous relationship between distance and time for a moving object:

So here we have a function of t that involves multiple powers of t and yet returns a dimensionally consistent result.
.....
However the taylor expansion part can be used to show that, when viewed as trigonometry, the sin/cos/tan of angles reguires an angle dimension depending on how you view it.
The Taylor expansion is often used to "show" this. Unfortunately, the process usually just takes the dimensionless (mathematical / numeric) form of the Taylor expansion and forgets how it is derived. A back-to-basics derivation from the differentials shows that the Taylor expansion is effectively unit neutral.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
now now Stuart you are being a bit naughty there. Your example equation, with the parameters included, returns 'm' meter values for every term in the polynomial! The earlier example I agreed to had no units on the parameters. The hidden issue is in the way that Quantity Calculus is playing with the pebbles - it wrongly, in my mind, separates the measurement number from the unit and its dimension, when they are all an integral part of the single measurement - your examples are polynomial, while typical QC is demonstrated on monomials, so the associativity is removed as an issue (no plus or minus in monomials;-), and the commutivity can be used to allow separability, just as long as you don't re-introduce the polynomial associativity problem.
The Taylor series expansion is identically the same issue, just seen from the other side (*). It (and you) says that each of the expansion terms are unit neutral (all terms evaluate to the same dimension), when treated properly. Thus for a Sin() the output is a pure number, so each of the terms of the expansion must evaluate to a pure number so the units&dimensions of the parameter and the derivatives must be kept in inverse proportion - most of the arguments are strawman arguments where that proposition was false at the start, so they then expand into the Taylor series (without regard for the dimensioning) and then claim it shows how either (a) the opponents proposal is wrong (despite the fact they set up the strawman!), or (b) that say radians can never have a dimension, such as angle. It's all a bit round in circles.
(*) the other side of the same coin, not a different coin - that'd be heads I win tails you loose, the old golden rule of 'my coin' 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Stuart,
An additional point about the Bridgman's theorem and the trig functions.
There is a problem with deciding what the Taylor expansion of the sin(Angle) should be if one rejects the apriori decision that Angles have to be in 'radians'. So for example sin(1.RA)=1, where RA is the Right Angle base unit, the expansion of sin(x) with x in RA's, can start to include an expansion of pi (and we go around the 'squaring of the circle' fun).
If the base unit (dimension) is flexible (not yet decided) then the differential of that must be included in the taylor expansion. This is where the use of a trignometric (geometric) Angle dimension drops in.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Edited to Add:
So a function like f(x):= 2•x2 + 3•x3 would be forbidden because it would try to add m2 to m3?
All is OK in Mathcad PM - see please More dimentions control
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Edited to Add:
So a function like f(x):= 2•x2 + 3•x3 would be forbidden because it would try to add m2 to m3?
All is OK in Mathcad PM - see please More dimentions control
Just to say that the function can be defined anyway we like (i.e. the parameters can have any units we want).
It is not until it is evaluated with a specific value (with or wothout dimensions) for the variable that the algebra system is able to detect and check that all the nomials have the same evaluated dimensional product term.
Stuarts original statements, and my response, didn't make it clear at what point(s) the validity and invalidity occured.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yep.
From Stuart's file: https://www.ptcusercommunity.com/servlet/JiveServlet/download/86229-11630/Test%20-%20Units%20Angles%2002%20extract%202.m… There are a margin note about SiUnitsOf, instead UnitsOf. Here not a magical unit appear, but preserve the argument unit. I guess that is not correct, but a good approach. I guess that the most correct option is introduce new dimensions: this is ln(m) as new one, ln(kg), sin(m), etc.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One problem from one serious problem book on math for students.
There is a function. It is necessary to determine the value of the argument for which the function is greater (less, equal etc) than its derivative.
When I say to mathematicians, that it is impossible to compare a function and its derivative, that it is better this proble (taking derivative and sole a inequality) to form another, without breaking the law dimension, that I find boring.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
The problem with your argument is that [y] is not (generally) equal to [x]/kg. Let's revert to the standard [t] = s, [x]=m, [y]=m,
Hi Stuart.
This is not the case, the standard here isn't [t] = sec, it's just a geometrical parameter, not the time. What the picture shows is that t can have another dimension than the one that make [t]^2=1, at least with this definition of sin and cosin. Further t is an angle. For mechanics, where t is the time, you never take sin(t), but sin(w*t), where w is the angular speed. If you see some equation in mechanics with sin(t), and t as time, it's implicit a factor of 1 rad/sec multiplying t. That's what's actually happen with the mechanical interpretation of parametric curves: they are traveled at one rad/sec. But if you need them at some other speed, need to introduce another value as the omega factor.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
StuartBruff wrote:
The problem with your argument is that [y] is not (generally) equal to [x]/kg. Let's revert to the standard [t] = s, [x]=m, [y]=m,
Hi Stuart.
This is not the case, the standard here isn't [t] = sec, it's just a geometrical parameter, not the time.
OK ... my own assumption here - show a physicist with the notation dsomething / dt in the context of a discussion involving "standards" and there is rather a tendency to think of "t" as time (ISO 80000-3:2007 3-7 symbol t = time). ![]()
.... What the picture shows is that t can have another dimension than the one that make [t]^2=1, at least with this definition of sin and cosin. Further t is an angle. For mechanics, where t is the time, you never take sin(t), but sin(w*t), where w is the angular speed. If you see some equation in mechanics with sin(t), and t as time, it's implicit a factor of 1 rad/sec multiplying t. That's what's actually happen with the mechanical interpretation of parametric curves: they are traveled at one rad/sec. But if you need them at some other speed, need to introduce another value as the omega factor.
Putting aside the discussion about whether trig functions (or any function) can take dimensioned arguments, I was addressing the fact that the differential equations as you presented them are not dimensionally consistent. Using quantities of dimension 1 simply hides this dimensional inconsistency rather than addressing it. The equations *require* the dimensioned scaling constant to make them consistent. When added, the "Can''t Be" expression in your derivation becomes a "Can Be"
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
..I was addressing the fact that the differential equations ... ? dimensionally consistent. Using quantities of dimension 1 simply hides this dimensional inconsistency rather than addressing it. The equations *require* the dimensioned scaling constant to make them consistent.
Philosophical point (*).
The 'scaling constant' between a base unit (concrete physical) and it's associated Dimension (abstract, conceptual) is unknowable, and could only be represented by a parameter, rather than a number. Thus 1.m = k . [Length] ; the value of both k and [Length] (the dimension) can never be know in anything other than symbolic form.
This philosophical point then extends to that 1 thing. It is missing a proper symbolic name and represents itself as a quasi-number, causing most people to leave it out. When given (or we are allowed to give) a proper name (or names, given there are many distinct uses of 1 ), and a choice of representative units (given we can't decide which, if any, of them is to be the 'base' unit), we can then recover our composure and properly extend the units and dimension systems within those computer tools and software packages that do include algebraic checking to have a wider benefit.
Philip
(*) I hope I've used 'philosophical' in the right sense.
(**) there's still a need for such tools to include a help/instruction manual with clear guides on how to convert old 'empirical' equations into mathematical and scientifically rigorous unit and dimension aware equations 😉
(***) I'd go (for angle base) for the <wink> decimal History of the metric system - Wikipedia, the free encyclopedia Angular Measure of the grade( and centi-grade, and milli-centi-grade) which is clearly an SI unit and rational on the circle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Stuart.
That's true, but what you prove it's that sin and cos can't get dimensions, like any other unary function in physics or math. For example, the minus unary function, or the factorial or gamma functions. Why do you expect that after apply -(5 sec) they go to be transformed to - 5 meters? Same thing with x or y, which goes to be applied to some argument, can't make some units to be appear after their application.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
..what you prove it's that sin and cos can't get dimensions, like any other unary function in physics or math. [????]
Alvaro.
Alvaro,
There is a BIG problem with these trig functions in that the broader community does not agree what they define or how they are defined.
Some argue that f(x) = x - x^3/3! +x^5/5! - ... defines the sine function, while others argue that sine (angle) = Opposite / Hyponeuse of a plain plane 'tri-angle' (that's three angles 😉
The mathematicians, who have no named dimensions anyway, start with the former, while those who navigate the real world (and Physicists) tend to side with the latter.
Each is a strawman (Straw man - Wikipedia, the free encyclopedia) to the other. Choose your starting point to prove 'your' point!
xkcd: Purity ; xkcd: Certainty ; xkcd: Powers of One ; <smile>
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Philip Oakley wrote:
Alvaro,
There is a BIG problem with these trig functions in that the broader community does not agree what they define or how they are defined.
Some argue that f(x) = x - x^3/3! +x^5/5! - ... defines the sine function, while others argue that sine (angle) = Opposite / Hyponeuse of a plain plane 'tri-angle' (that's three angles 😉
Sure, for this reason I state that one must to say about which definition of the function one is taking about. The fact that sin can be developed in such way is using reals, but units actually don't need those numbers, units need only rationals. See my old answer to you document here: Re: Why is Mathcad so Keen on Units? . There, also, there are a Mona's post saying that take in consideration this document for further develop in mathcad (2010 year). If we have that, the ability to introduce new dimensions in mathcad, we probably are playing introducing a dimension like ln(distance) with some unit like ln(meter). I don't se in my old ruler calc ln(x/cm), I see only ln(cm):

Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz написал(а):
I don't see in my old ruler calc ln(x/cm), I see only ln(cm):
Best regards.
Alvaro.
Welcome to Re: Nostalgia - a slide rule
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For those young 'uns that would like to have a go at the 'slide rule' experience, try the http://www.scientificamerican.com/media/pdf/Slide_rule.pdf which make a nice little slide rule out of an A4 (or letter) sheet of paper. It's nicely self aligning. If you use a higher 'weight' (stiffer/thicker) paper it feels quite nice.
Philip
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Phillip for the present.
Just an experiment. Ask to someone for the units of, or which unit could represent C ( x ). Then ask for the units of B (x^2), or C1 (1/x). Finnaly ask for the units of T (ln(x)).
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dominique Bauer wrote:
Back to the main point of this thread.
I was hoping that someone at PTC Mathcad would say something like: “Dear Dominique, You may have a point. We will consider your suggestion and may modify the factory default setting of the font for units to roman (upright, not bold, blue color) in the next release of Mathcad."
Agreed. It would be so nice if....
However, years of experience suggests it may not happen...
It's often said that many user communities are there so that users can gripe among themselves and feel better for getting it off their chest without the companies actually doing anything about the issues. it appears that the bigger the companies get the more likely it is to be true.
Maybe they will open source an older version... Ahh, hopes and dreams.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was hoping that someone at PTC Mathcad would say something like: “Dear Dominique, You may have a point. We will consider your suggestion and may modify the factory default setting of the font for units to roman (upright, not bold, blue color) in the next release of Mathcad."
As others have noted, that is very unlikely to happen. There are two feature lists for future Mathcad versions: one that details what users want, and one that details what PTC has decided users want. There are big differences between the two (partly because PTC is more interested in Mathcad features that Creo users want than Mathcad features that Mathcad users want). Unfortunately, this isn't new. Mathsoft had the same problem, albeit to a lesser extent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Philip Oakley wrote:
StuartBruff wrote:
.. but you cannot calculate the sine of 2kg.
I disagree ... must get round to writing up it up one day ...
Hi Stuart,
Ah, the misunderstandings and bad groundings of Quantity Calculus.
Unfortunately, Quantity Calculus, as it is promolgated makes the error of splitting the arithmatic from the 'dimensions' (note I said arithmatic rathers than mathematics;-). This wrenches the whole units, dimensions and scalings away from being a well defined and integrated system.
http://web.ist.utl.pt/ist12219/data/60.pdf Two alternative derivations of Bridgman’s theorem, Mario N. Berberan-Santos and Lionello Pogliani, Journal of Mathematical Chemistry 26 (1999) 255–261
Those people prove something more strong than any unidimensional unit must to be write as a*[x]^b, they prove that any univariate function must to be write as f(x) = a*x^b ! Check de demonstration, please. That's make engineering much more easy.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
Those people prove something more strong than any unidimensional unit must to be write as a*[x]^b, they prove that any univariate function must to be write as f(x) = a*x^b ! Check de demonstration, please. That's make engineering much more easy.
I think you missed one hidden point. They showed that when 'x' has dimensions, then by the "principal of dimensional homogeneity", the function of 'x' must be of that form.
The reverse is not true. if x has no dimensions (i.e. pure number) then it can be a polynomial. (see the footnote about Descartes)
The other part that isn't explored is the multivariate case where we can have the case (usually for Length, see Descartes) where we can get the form f(x,y) = k.(x^2 + y^2), but it is (must be) homogeneous for the situation to be valid. (which, via Descartes) leads to the Angle vs Length, vs number of D/dimensions fun!).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Philip.
Check with a counterexample. Let f(x)=A*exp(B*x). Assume x has time dimensions, and f length. Given that f have infinite derivatives, has a Taylor develop. Obviously, A and B have dimensions too, but the important thing then are: f and x have units, and exist the Taylor develop of f: ¿then f must to be a monomial? That's what I see between steps 13 and 20. The conclusion can't be more clear: never start a proof in the step 13, it could bring bad luck. Or maybe the conclusion is that can't play with infinity in that way: maybe meters plus meters given meters, but adding an infinity of meters the situation is more complicated.
About Descartes and the other path, it is different, and more strong the proof, and not use calculus (units don't need calculus, actually don't need the real numbers, is a rational problem). Descartes found the concept of algebraic curves, and he don't see squares or cubes, just see algebra. So, probably he don't see logarithms in the calculus rule (regla de cálculo, which is the name in spanish for this rule).
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
Check with a counterexample. Let f(x)=A*exp(B*x). Assume ..
We cannot (should not) start at that point because it 'begs the question'.
It should be that some experimental measurement Y appears to be some function of a measurement X (taken at the same time). Then the taylor expansion idea can be taken forward to determine what the functional form must be between Y = f(X).
At each step of the differential expansion (of the results), we determine a coefficient for each power term of X, and in every case, the coefficient must have the right corresponding dimensions such that the overall term has the dimension of Y.
When the dimensions of the coefficient is burried in all that dimension "1" stuff, then the dimension information gets lost.
In particular the name of the thing being dimensioned get's lost.
If we insert the "1[dimesion]" into the pure form then it (the scaling of the coefficiienst in terms of that 'dimension') all pops out quite nicely.
I was going to give an example but we then get into needing units of Neper for real X, or if we are soing the sine via exponential, we need Angela and we also need 'imaginary' dimension to complement the unity "1" dimension.
If we remember the purpose of dimensions, from a Mathcad perspective, it is the automatic checking of formula for consitency, without the need for special names and symbols and their use cases and exclusions (see http://www.bipm.org/en/publications/si-brochure/section2-2-2.html Even acknowledges the likelihood of mistakes because of Hz! And that's official)
The key point for me is to get to the situation that acknowledges that capability and possibility - a formal algebra that covers dimensions)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Philip.
When the dimensions of the coefficient is burried in all that dimension "1" stuff, then the dimension information gets lost.
Correct math set up the correct dimension for each coefficient:
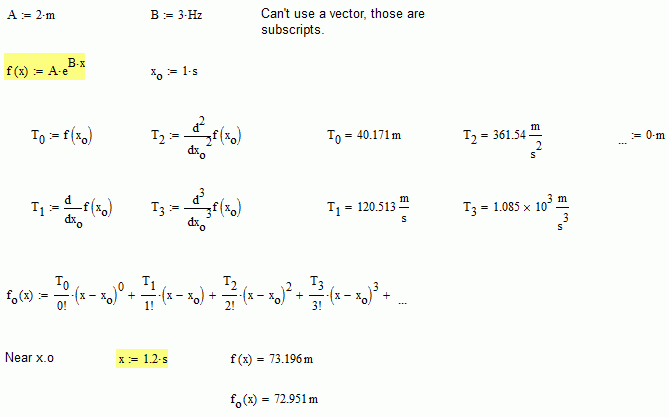
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
Hi Philip.
When the dimensions of the coefficient is burried in all that dimension "1" stuff, then the dimension information gets lost.
Correct math set up the correct dimension for each coefficient:
"Correct math set up the correct dimension for each coefficient:"
*That* is exactly what I've been saying all along (ie, over a decade). If we have to have to have special rules for dealing with a particular quantity (eg, angles), then (IMO) there is something fundamentally wrong with the corresponding quantity calculus (where the word calculus is used in a generic not familiar ("diff and int") sense).
The important fact that is lost in most "Proofs by Taylor Expansion" is what the Taylor series is and where it comes from - that is, a means for determining the coefficients of a function's power series representation.
The correct starting point is to assume that some function can be represented as a power series and, to be dimensionally (ie, physically) consistent, the coefficients *must* balance the powers.
I fail to see what inherent difference it makes to the physics of the situation whether we have,
f(x) = 3 x
s(t) = s0 + u.t + 1/2.g.t^2
s(t) = a0 + a1.t + a2.t^2 + a3.t^3 + ...however many other derivatives are considered necessary to model the behaviour, which might very well turn out to be equivalent to ...
s(t) = sin(t) (in it's series expansion form that I couldn't be bothered to type in ... )
Everything else gives the appearance of "magic" ("Here Be Dragons (angles), ... and they don't care about physical consistency, so we just pretend they're dimensionless do some pure maths, and then we'll add the dragons (angles) back in again and everything will be OK!").
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think we are talking at cross purposes again.
If you define a function, and its polynomial expansion, with purely real coefficients (i.e. without dimensions) then by definition you have already decided that it is a dimensionless function. Almost all these pure maths examples fall into that category, which is somewhat to be expected as pure maths doesn't have dimensions anyway.
In my case, I am defining the function by its (science and engineering) purpose, so the sine (of an angle) is the ratio between the side opposite the angle and the hypoteneuse of a right angle triangle for geometric and navigation style calculations, so we get that the Sine of half a right angle (aka 45 deg) is one over root two (i.e. an angle converted to a number), etc. We don't get to creating a polynomial expansion till later, which is the point at which the units within the polynomial coefficients arrives (if done that way, we can use trig functions).
Many years ago Tom Gutman pointed out (in one of these threads) that effectively we end up with two of each function, the dimensionally aware Sine, and we get the mathematicial's polynomial they call sin(). They start from different perspectives.
If we use a mathematicians perspective to define how the dimensional algebra should be performed, we will continue to have these Dragons 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The other aside has to the the rhetorical question: But what makes Angles actually show up in the otherwise reasonable dimensional stuff?
It is my view that the souce is the same as that Descartes reference, where he shifted away from geometry (where area is not volume) to x, x^2, x^3 all being on the same number-line. It could even be traced back to Pythagarus who has lengths running in all directions (opposite, adjacent, & hypoteneuse), so we get a 3d space being measured with only a single SI Dimension.
This use of a single SI dimension to cover 3 real dimensions means we get cancellations of terms during division (of orthogonal independent lengths) which would never happen with any of the other dimensions - if we could we would simply cancel kg/s 'because' kg, s, and K are three common dimensions and we can always combine 3 into one, just like 3d Length (but we don't). The qustion becomes why do we allow it to happen to lengths, and what should we do about it (the inappropriate cancellations in 3d geometry calcs).
An appropriate method for handling major errors in practical engineering calculations that involve 'angles' is necessary (e.g. I've seen arbitary 4pi values thrown in just for fun to get a wishful answer), and should be part of Mathcad. If Mathcad claims to be able to provide units and dimension checking then it must be able to handle normal irradiance and radiance calculations without confusion. If a Quantity Algebra can't handle it then it has failed.