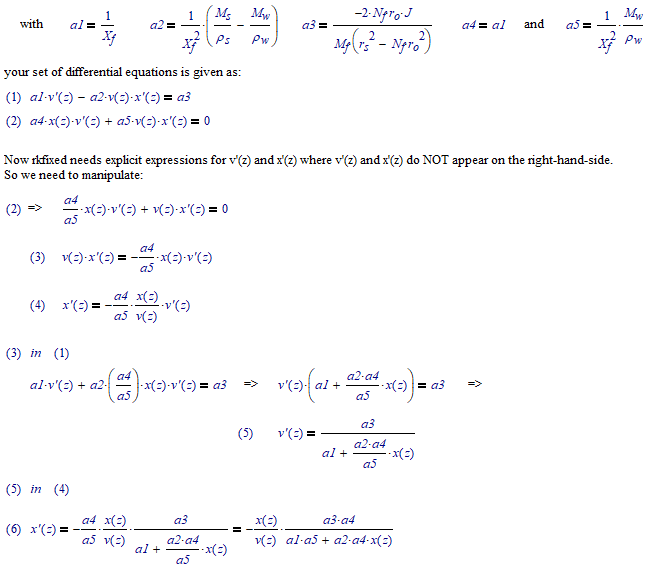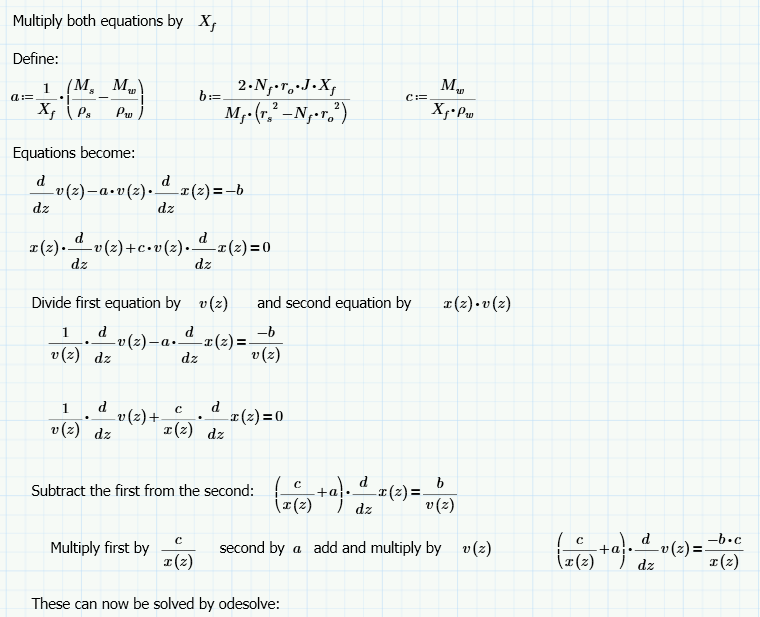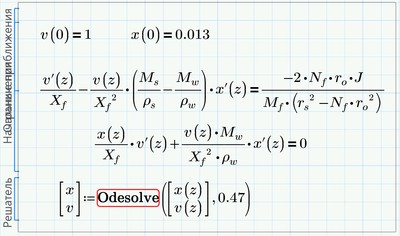Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Using rkfixed in mathcad prime 2.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using rkfixed in mathcad prime 2.0
Greetings!
I want to solve this problem using rkfixed function in mathcad prime 2.0. Help would be highly appreciated!
I am having trouble understanding the derivative matrix of this function
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK I found them (they are there today, they weren't yesterday. I wonder where you grabbed the second from...because both equations define v(z)*x'(z). And I wonder why you use d v(z)/dz on one occasion, and all other derivatives use prime notation: v'(z) and x'(z)...?
Anyway, here goes:
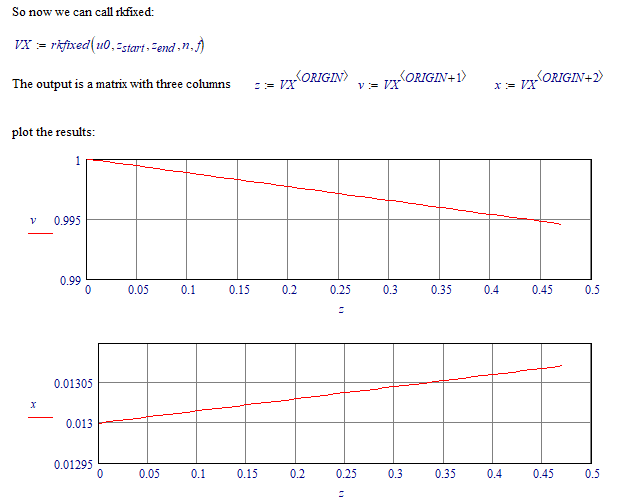
With such results choosing 47, 470 or 4700 steps makes no difference in the graphs.
Possibly not the solution you expected. I suggest you check your differential equations once more.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think first you have to clear up what the function x'(z) is. It is not defined. Do you need to solve two functions ( v and x) simultaneously (which isn't impossible, but requires a set of functions to rkfixed.)?
I suggest you look up the example for "Solving a First-Order ODE Initial Value Problem" in the help. That should explain the usage of rkfixed.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Right! I have two equations which contain v(z), v'(z), x(z) and x'(z)
the rest constants are known
initial conditions are known: v(0)=1; and x(0)=0.013
I need to solve it from ini=0 to end=0.47
I need assistance in forming the derivative matrix. It would be highly appreciated!
Further in the first equation we can assume the value for variable x'(z) as a constant as 0.5 and put the values of v(z) and v'(z) in the second equation to obtain x(z) and x'(z) then iterate the procedure.
I need to use rkfixed to do this.
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With x(0)=0.013 that makes c=0.013.
So x(z)=0.5z+0.013.
Who needs rkfixed?
Luc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
x'(z) is not 0.5 we can assume it for simplicity if necessary in the first equation.
.
We have to solve these equations simultaneously and check for error between the values until tolerance of 10^-10 is achieved and find values for v(z) v'(z) x(z) x'(z)
i.e. assume value of x'(z) in first equation for one time only and find value of v(z) and v'(z) from first equation
then put them in second equation to find x(z) and x'(z)
and after that use the value of x'(z) in the first equation again to find values of v(z) and v'(z). Check for error between these two sets of values calculated for v(z) and v'(z)....if the error is less than 10^-10 we can stop. And repeat until the tolerance is achieved.
BUT if a second method is there, help would be appreciated.
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With two functions to solve, v(z) and x(z), you need a set of two differential equations. So far I remember seeing only one differential equation, that's not enough.
Please provide the two differential equations involving the derivatives of v(z) and x(z), preferrably using ONLY symbols on a Prime sheet (NOT just a picture). For now I don't need the values of any constants...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes There are two differential equations in the sheet and thats all there is to the equations
@ValeryOchkov If that command in odesolve would somehow work it would also be good, but I still require a solution with an odesolver such as rkfixed or Adams
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK I found them (they are there today, they weren't yesterday. I wonder where you grabbed the second from...because both equations define v(z)*x'(z). And I wonder why you use d v(z)/dz on one occasion, and all other derivatives use prime notation: v'(z) and x'(z)...?
Anyway, here goes:
With such results choosing 47, 470 or 4700 steps makes no difference in the graphs.
Possibly not the solution you expected. I suggest you check your differential equations once more.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
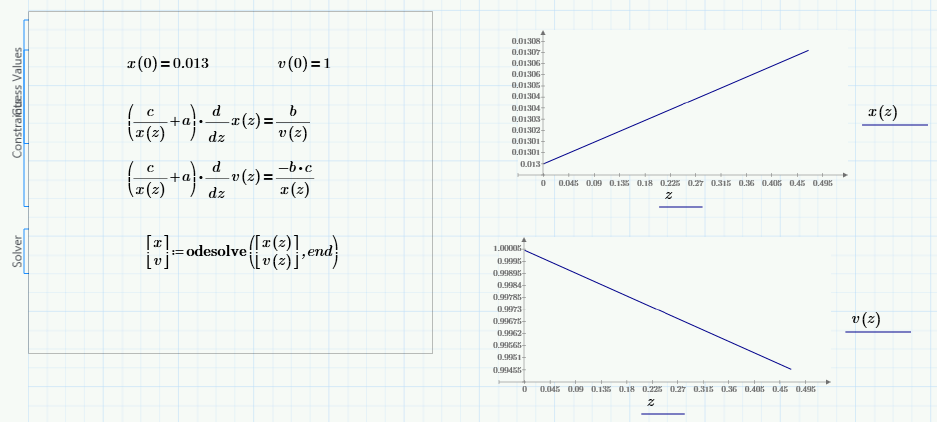
With a little manipulation these equations can be solved by odesolve.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which gives the same results as rkfixed... Two different methods giving the same results, improves confidence.
I've tried to see if a v(z) and x(z) could be linear functions (e.g. v(z)= b*z +c). Alas, that does not solve the set of DEs.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
...
I've tried to see if a v(z) and x(z) could be linear functions (e.g. v(z)= b*z +c). Alas, that does not solve the set of DEs.
No, they are not linear. They appear to be simply because of the magnitude of the constants. Increase Xf by two orders of magnitude for example (probably completely nonphysical!), and you see a distinctly non-linear output.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why do you not use units?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
because most of the times they cause a hindrance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried to solve the first equation but it gives an error saying about derivative function D that this function cannot be used here.
File is attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more try - with Odesolve - why not!