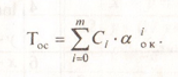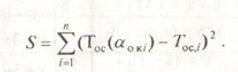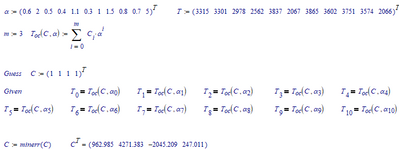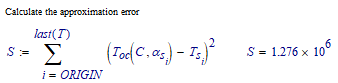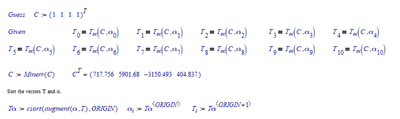Hello PTC fam,
I don't know where did I do wrong in this programe.
the question is
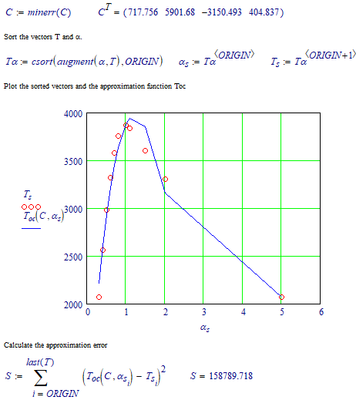
Determine least square method value of coefficients Ci( i=0,...,m) in polynomial form.
Calculate the approximation error where m=3
Please advice.
Regards,
Adlil
ACCEPTED SOLUTION
Accepted Solutions
Did you mean to do this:
Then:
Finally:
But there are options for minerr. If you press the right-mouse button on it, you can select other minimisation strategies. The above was done using 'Linear' (The default). For non-linear: Levenberg-Marquardt you may get:
Success!
Luc
Your sheet does not explain well what you are trying to achieve. Apart from that:
1. The summation for Toc in above picture goes from i=0 to m, when m=3, that means you should get C as a vector of 4 elements. Your sheet shows you calculate a vector C consisting of only three elements. The input for that calculation (matrix A and vector B) do not seem to be related to alpha or T.
2. Instead of the solve block, you can use the lsolve function to determine C from A and B:
3. What is the vector K calculated for?
Success!
Luc
Did you mean to do this:
Then:
Finally:
But there are options for minerr. If you press the right-mouse button on it, you can select other minimisation strategies. The above was done using 'Linear' (The default). For non-linear: Levenberg-Marquardt you may get:
Success!
Luc
Thank you for the reply. Pardon I should reconfirm back with you before hit the "accept the solution" button. I would like to ask
1. Does Gauss method is that simple ? Mind to explain why Gauss method we need to list like this compare to my version.
2. What is Minerr function is ?
3. Why do you sort vector T and alpha ?
Sorry if my questions didn't look smart since I really want to understand this program and the task given. Thanks again waiting for your reply.
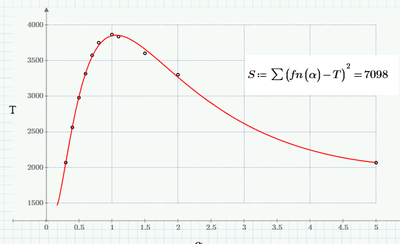
I've been playing with this. A direct least squares fit to this data with a third order polynomial isn't great. But a fourth order fit to the natural logs looks pretty good. (My apologies for diverting the discussion!) Sheet in Prime 4.0 Express.
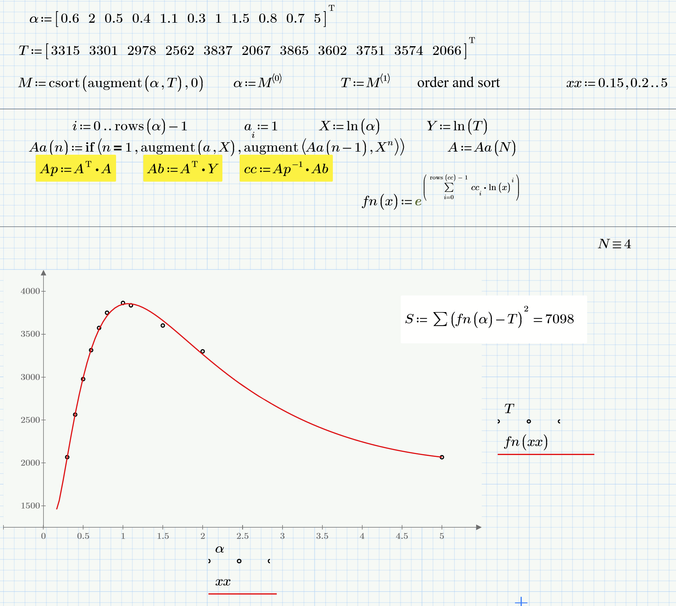
Here is a screenshot of Freds work (I just omitted the grid which can be achieved much easier in real Mathcad)
You can also create his function using Mathcads built-in polyfit function.
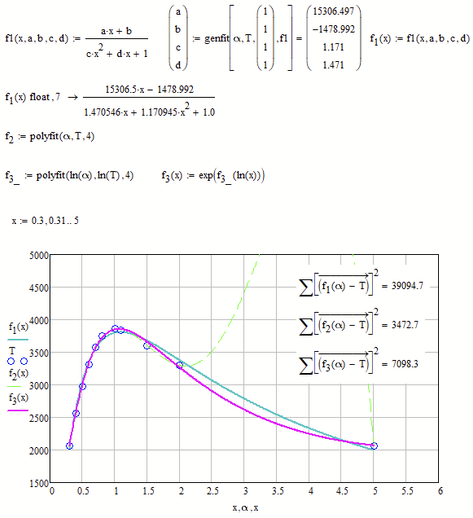
Here a comparison of a rational fit (f1), a polynomial fit of fourth order (f2) and Freds approach (f3).
According to the sum of squared errors the polynomial fit (f2) would win, but I bet you don't like the curve in the range from 2 to 5. So I guess that Freds approach rules.
MC15 sheet attached
