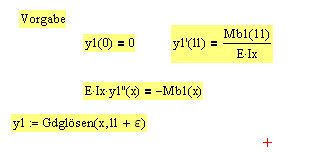Why do i get no Answer with the ODE-Solver in MC15?

[vlehner]

Hi,

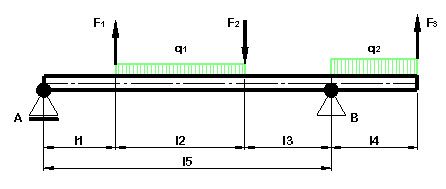
I have to calculate the deflection of a shaft with some different loads.

(a couple of Forces and line-loads like in the sketch below).

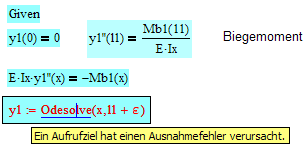
The diagram of forces and bending moments i could calculate completely, but when setting up the boundary conditions and the ODE it's running into an error.

Boundary conditions should be taken from the function for the bending moment.

Although i think i have set up all conditions completely, i can't display/calculate the deflection anyway.

I think it's because of the forces which act at particular lengts and their definition in the solve blocks but i have no idea whats wrong.

Has somebody an idea?

Thank you very much!

EDIT: I see more and more problems solving in good old MC15 hoping it lasts running for a long time.

[Werner_E]

Strange effect.

When I open your sheet i get an error message in German even though I have set my Mathcad to run in all English.

When I trace the error I am pointed to an expression where three numeric values are involved and the error messages tells me sometihing about an invalid array index.

I retyped the whole block and disabled yours and it seems to work. I have no explanation for this.

Editetd Worksheet attached.

[vlehner]

Hallo Werner,

Bei Deinem neugeschriebenen Lösungsblock ist mir aufgefallen, dass bei der Randbedingung des Biegemomentes die erste Ableitung steht. Es muß jedoch die zweite Ableitung sein.

Außerdem sieht dieses "l1" als das Funktionsargument des Biegemoments anders aus als das Argument in Gdglösen.

Nach Änderung der og. Punkte ist leider wieder alles beim alten:

Ich hatte das Ix auch komplett umbenannt, aber das hat auch nichts gebracht.

Erscheint mir alles auch sehr komisch.

Vielleicht fällt uns ja noch was ein, trotzdem schon mal Danke.

[Werner_E]

In der Tat, es war für mich nicht immer auszumachen, was ein kleine "L" ist und was eine "1". Ich hatte da einmal 11 geschrieben anstelle von L1.

Das wahre Problem ist aber die zweite Ableitung in Verbindung damit, dass es sich da bene nicht um eine Anfangsbedingung handelt (y1"(0)=.... wäre kein Problem). Damit hatte Mathcad schon immer seine Probleme.

Vielleicht hilft es, wenn du dir in der Hilfe das Kapitel "Deriving Initial Conditions for an ODE" mit den Funktionen "bvalfit" und "sbvalfit" ansiehst. Allerdings fürchte ich, dass das auch keine Hilfe sein wird, da mit y" ja die höchste Ableitung an der Endstelle vorgeben möchtest.

[vlehner]

Ich bin jetzt eine Stufe höher gegangen (Dritte Ableitung ist proportional zur Querkraft).

Damit kann ich alle Randbedingungen exakt angeben, erhalte jedoch eine exotische Fehlermeldung:

[Werner_E]

Exotisch - in der Tat.

Sieht so aus, als ob deine Randbedingungen "Odesolve" überfordern und es diese DGL eben einfach damit nicht lösen kann.

[vlehner]

---

@WernerExinger wrote:

Exotisch - in der Tat.

Sieht so aus, als ob deine Randbedingungen "Odesolve" überfordern und es diese DGL eben einfach damit nicht lösen kann.

---

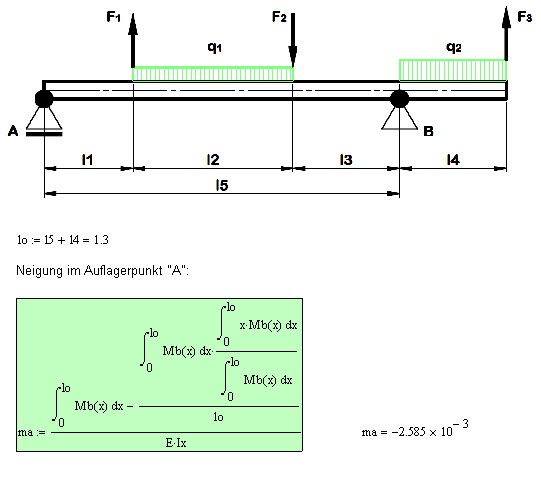
Now it seems that i found a way for finding the boundary condition in the left support: First i calculate the Area of moments and then i can calculate the slope.

With "ma" i have the condition and again an ODE of 2nd degree.

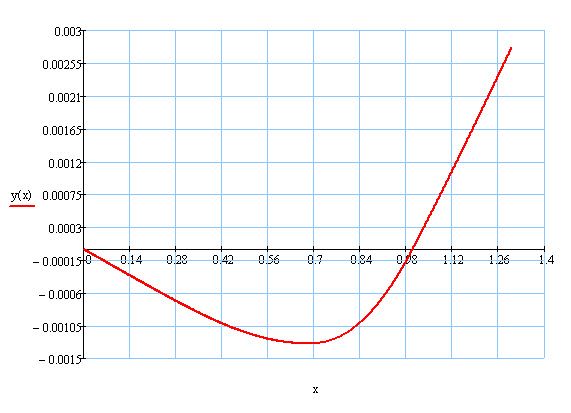
The graph of the deflection seems to be plausible, it goes at least into the right direction but the ammount of the maximum deflection is not right so i have to test some other things.

and the deflection:

[Fred_Kohlhepp]

Your expression for the angle does not unit balance.  I was thrilled to see you had a method of determining the end slope--that would make this type of problem much more ammenable in Mathcad.

I started a simple beam model (simply supported uniform load) and discovered this flaw.  For some reason I can't paste images today, I'll try to attach a zipped version 15 file.

[vlehner]

Hi Fred,

I have this method from my good old textbook, where such problems are discussed.

With the roarks-formulas, i can't evaluate (see) a perfect solution because my problem is a bit more specific and has more forces and more line-loads.

The example of roarks-formulas for bending problems have at any example only one force or one line-load.

[Fred_Kohlhepp]

There is the "principle of superposition."

The assumption (for elastic stress analysis) is that the system is linear, an applied load produces a proportional strain/deflection/rotation.  As long as that assumption is valid, then the strains/deflections/rotations of multiple loads can be superimposed (AKA added) to get the combined result.  So, if you can describe a case from Roark for each of your load conditions, you can combine the results to get the combined case.

[vlehner]

Superposition  is a good argument.

Calculate each single angle which is caused of each single load and summarize them all.

The tangens of these sum is the desired slope.

Thanks Fred, i will try this now.

[Fred_Kohlhepp · Accepted solution]

Superposition should give you the deflection curve as well.

[vlehner]

---

@Fred_Kohlhepp wrote:

Superposition should give you the deflection curve as well.

---

Superposition was the keyword in a strong answer.

Thanks Fred!