Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Why the solver fails?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why the solver fails?
Hi All,
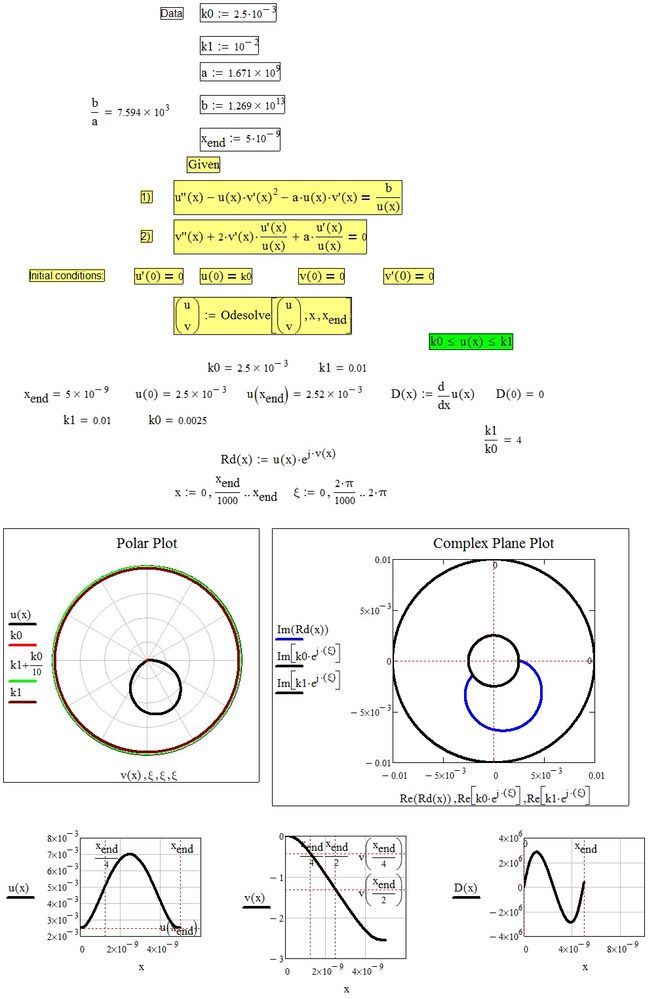
Why the solver fails if I insert, into the solve block, the constraint highlighted in green ? And how to correct it?
What to do to have the polar plot equal to the complex plot below depicted?
Thank you very much.
Frank
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe a problem with MC15 autoscaling
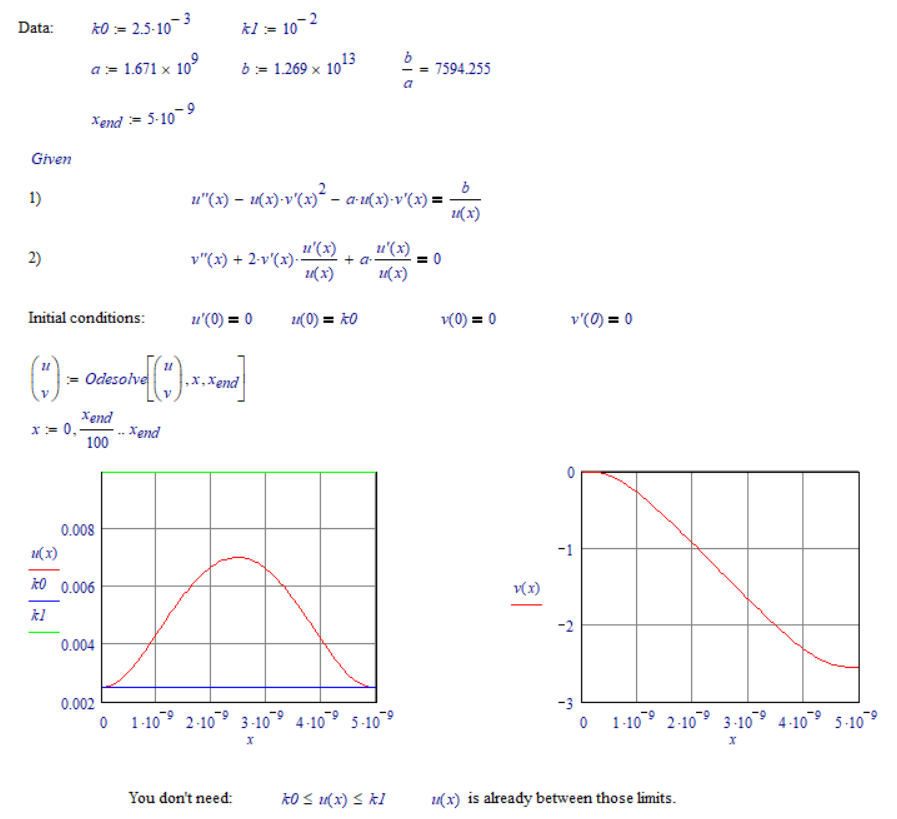
Klick in the plot and at the right you will see the value 2.5x1o^-3. Change it to 0 and see if that helps
And yes, the k0 are the same. But one is formatted ad variable and the other as constant. Should not do any harm in MC15.
But the condition you demand k0<u(x)<k1 is a global condition. Can't image that a primarily locally working numerical algorithm would be able to fulfill that.
Its not even possible to demand e.g. u(10^-10)<k1. The error message we get is misleading as so often in a solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You k0 in 'u(0)=k0' is a different k0 when you define it at the top: 'k0 := 2.5 * 10^-3'.
And:
Note that the results of Odesolve are ONLY valid between the defined endpoints, 0 and x.end in your case.
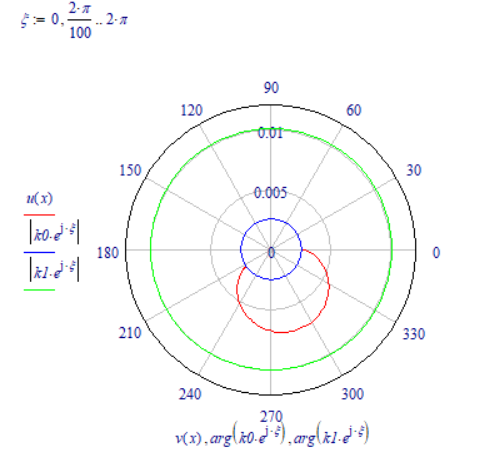
And your polar plot to correlate with the 'complex plot' is:
The argument(s) to the left descibe the magnitude, those to the bottom describe the argument (angle).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
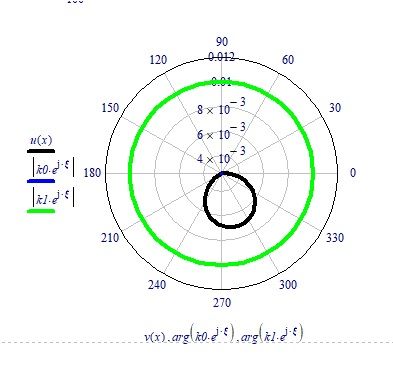
Thanks Luc, but once opened the attached file, with Mathcad 15, the polar plot is this (I've only modified the trace thickness):
that is, there is no change compared to the old one.
So what to do?
Furthermore I believe, insted, that k0 is the same!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe a problem with MC15 autoscaling
Klick in the plot and at the right you will see the value 2.5x1o^-3. Change it to 0 and see if that helps
And yes, the k0 are the same. But one is formatted ad variable and the other as constant. Should not do any harm in MC15.
But the condition you demand k0<u(x)<k1 is a global condition. Can't image that a primarily locally working numerical algorithm would be able to fulfill that.
Its not even possible to demand e.g. u(10^-10)<k1. The error message we get is misleading as so often in a solve block.