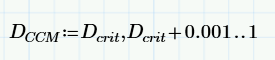Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Why wont it graph?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why wont it graph?
I have a piecewise non-period behavior that I'm trying to express by using two intervals but all I get is a blue dot for the second trace if the spacing its space is defined to be other than the default value of "1". Do I have to use logic statements to graph piecewise if I don't want a spacing of "1" between points to graph on my blue trace?
It seems I'm strictly limited to the array in purple for subsequent plot lines after the first? I guess that's O.K. for plots with a magnitudinous domain but I only want to plot up to "1" so it is a bit inconvenient.
Thanks in advance for your guidance...
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The second line does not graph as the definition of DCCM is wrong. Corrected it looks like this.
Then you get the second line on the graph.
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The second line does not graph as the definition of DCCM is wrong. Corrected it looks like this.
Then you get the second line on the graph.
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. I was struggling with that for like an hour.
Might you know how I can clean up my return values for the solve statement? I can't seem to get "assume = real" to work. Or "D < 1" to work either 😞
What am I missing (besides your most timely and heroic help)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Reduce the equation by performing the arithmetic you can do. Then solve. You get real values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I appreciate you double dosing me with your competence. As far as manually simplifying, that sounds a bit too much like actual work for me to consider it a go to. Anyhow, thanks a lot...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using the modifier "float" forces the symbolics in some sort of inexact mode but results in pure real solutions without the small imaginary part. But the symbolics will still ignore the "assume, D<1" statement and return all 3 instead of just two solutions.
But as you are after a numeric value only, I wonder why you think you have to use the symbolics.
You may use one of the numeric methods provided by Prime - either the "root" command or a solve block:
As you can see the "root" command's result is a little bit inexact. You can make it better by setting the system variable TOL to something smaller than the default value 10^-3. If you set it to 10^-7 you get the same result with both numeric methods.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you again Sir for lighting the way for me. You know my main reference is a book entitled Essential PTC Mathcad Prime 3.0 by Brent Maxfield, P.E. Have you considered writing a text yourself? You seem to have all the answer and I'm sure could readily fill a volume or two. All of us that you've helped I'm sure would be well inclined to purchase such an offering. There are many such little snags that could be better documented.
Anyhow, I'm generally disinclined to use the solve block because it is just a little bit goofy and unwieldly to me with the overlapping vertical text there, the guess value necessity, and the regions that expand at some prespecified rate established by PTC. I am admittedly an unabashed novice but I don't like those things on my worksheets even though they may indeed be powerful. I think they are needed for differential equations if I'm not mistaken so I might fiddle with them some in the distant future... Your root approach is most amenable to me Sir.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The "root" command looks more straightforward and give the desired result in case of your task. And I agree, that the solve block looks much uglier in Prime than it used to do in real Mathcad (version 15 and below). But despite the need of a guess value, a solve block usually gives you more control as you can add more and different constraints (like the "0.1 < D <0.9" I had shown). Also a solve block can not only be used with "find" but also with "maximize", "minimize", "minerr" and, as you probably know, with "odesolve". So even though its bad looking its a very powerful numerical tool.
A symbolic solution sure may be desirable but often the tasks are to complicated for a symbolic solution, especially as Prime uses quite old and limited symbolics (a very old version of muPad).
BTW, writing a book about Prime would not make much sense. Not only from the pecuniary point of view, but mainly because, sad as it may be, we have to realize that Prime is a dying piece of software since since it was acquired by PTC.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Google trends surely shows a decline in its popularity since peaking in January of 2014 and PTC appending the current version number with a third digit so that it is now all of "5.0.0" sure does seem to spell disaster for further development.
It is too bad because I'm just getting started with Prime after unsuccessfully trying to learn sMath. I switched to Prime because in my personal experience the learning curve has been gentler. Do you mind if I ask you what your post Prime plans might be? Will you be running original Mathcad indefinitely do you think?
Someone in the sMath forum said that PTC disabled all of the extensions that he had bought legally for Mathcad 14. Anecdotes such as those make me even more weary about not having a perpetual license for my worksheets. How would I access my worksheets in the event that Prime is discontinued and subscriptions can't be bought anymore?
I'm curious as to if there is any legislation dissuading corporations from hanging their old customers out to dry with regard to obtaining subscription based licenses for defunct software. Will Mathcad Prime subscriptions be forever available regardless of the products life cycle?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am using Mathcad since version 2.0 - note, I mean Mathcad, not Prime and 2.0 was running under DOS 😉
I never used Prime for something serious. I installed it because I had to opportunity to do so, because I am/was curious and I fire it up nowadays mainly for users in the forum here if they have a question about it.
At the beginning more than 10 years ago there were already rumours that PTC would not have in mind to further develop Mathcad as a stand alone product but rather wants it to act as a math add-in for Pro-E / Creo. Like so many others I ignored the warning signs and did not want to believe that a piece of software so ingenious and powerful (and its users) would be treated that bad by PTC. Now we know better and I can't imagine anyone believing that Mathcad will rise like a phoenix from the ashes again - not as long as PTC owns Mathcad.
Furthermore the licensing scheme changed and PTC does not sell any perpetual licenses any more. So as a new customer or if you want to use the latest version, you have to pay an annual fee to have access to your own IP, your worksheets. Thats an additional reason for looking for alternatives.
In my case I will keep up with Mathcad (sure not Prime) as long as possible and hav in parallel a look at Matlab and, for harder symbolic needs, Maple. But of course there is no software which could match with Mathcad when it comes to ease of use, self documenting whiteboard interface, etc.
SMath sure is worth a look, too. The symbolics there is very weak and you have to put in more work to pimp it up with useful add-ons (there are alot of useful ones), but SMath seems to have a growing number of capable contributors, a very lively user scene and in contrary to Prime its a software which is supported and developed further. And best of all - its free 😉
Anecdotes such as those make me even more weary about not having a perpetual license for my worksheets. How would I access my worksheets in the event that Prime is discontinued and subscriptions can't be bought anymore?
I'm curious as to if there is any legislation dissuading corporations from hanging their old customers out to dry with regard to obtaining subscription based licenses for defunct software. Will Mathcad Prime subscriptions be forever available regardless of the products life cycle?
I am sure not an expert in legal questions but I guess that you can't force a company to sell you subscriptions or make their software freeware in case they decide to stop development. They sure will sell you subscriptions as long as they can benefit from doing so, though. Losing your work completely if you don't renew subscription on a regular basis is a problem you are faced today in many cases as many companies go the subscription way and don't sell perpetual licenses. Sure this is only done for the benefit of us users as the companies wants us to be able to always benefit from the advantages of the latest versions of their software.