Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
asymptote + odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
asymptote + odesolve
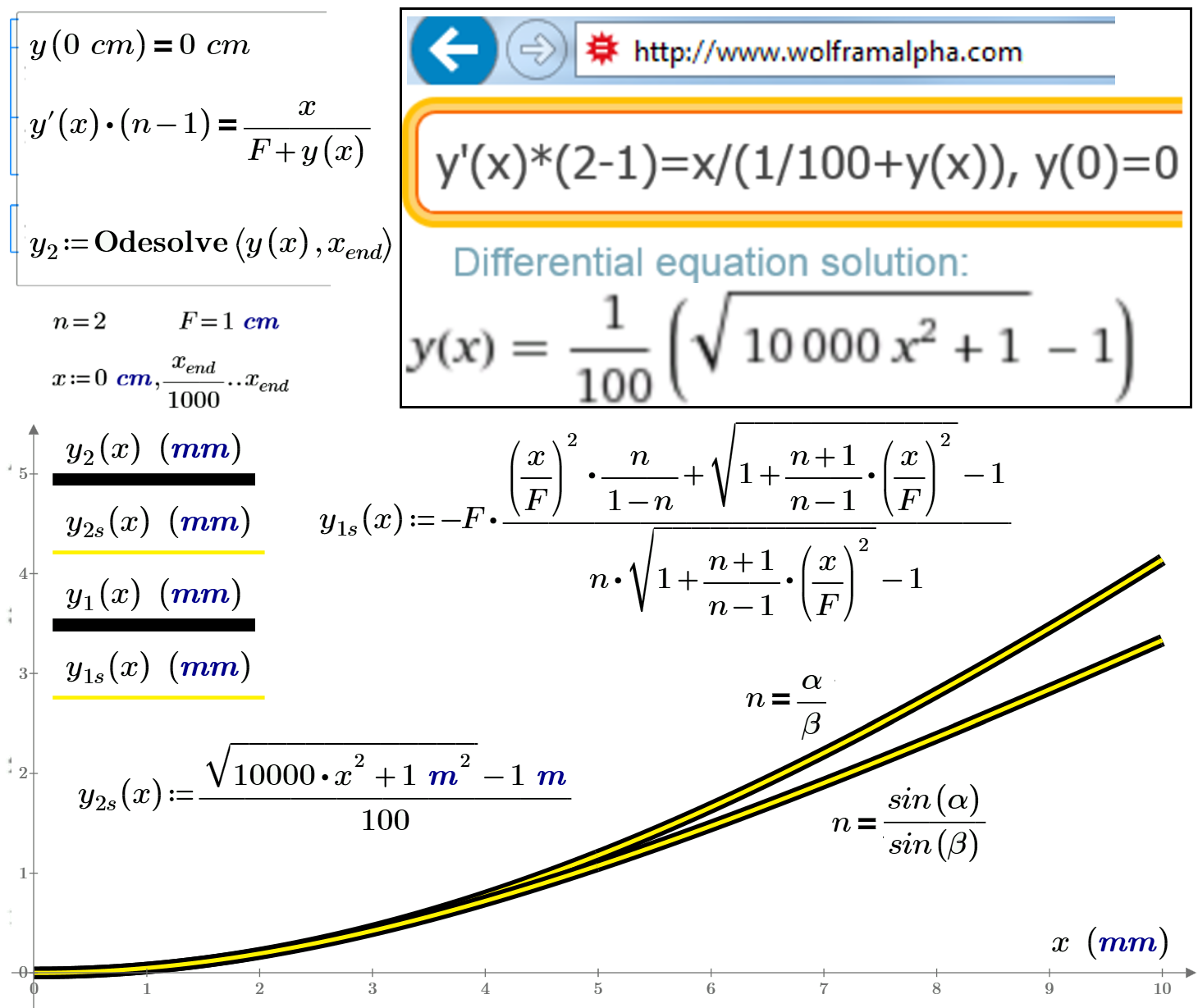
Is there a way to find an asymptote of a function created by the Odesolve function

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you.
I think it's a great honour to be named second in place after Christiaan Huygens.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
The right-sided asymptote is:

Provided you make sure that F is the point on the y-axis where your focus lies.
In your case F would be -10 (mm).
To get a two-sided asymptote, just replace x with sqrt(x^2).
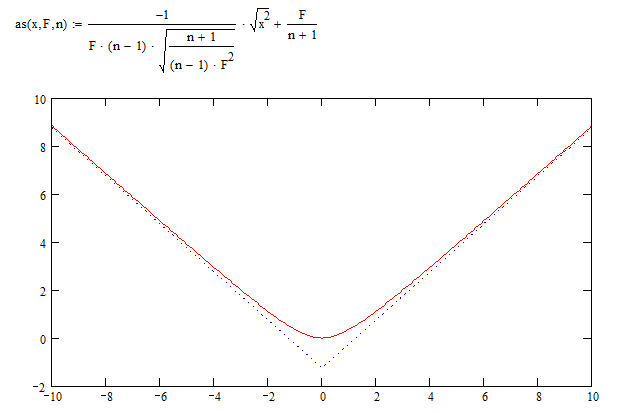
This plot was made with dimensionless numbers, F= -3, n= sqrt(2).
Regards,
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Luc.
Happy NY!
But I think about the red function, not black.
Val
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
The asymptote I gave IS about the y1 function, not the y2....
Note that for the black function, the asymptote goes through (0,-10mm), whereas the y1 asymptote goes through (0,-10/3) for your values of F=1 cm=10 mm and n=2 according to the function I provided: F/ (n+ 1)= -10/ 3.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Hi Valery,
The asymptote I gave IS about the y1 function, not the y2....
Luc
And what is an analytical view of this function?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok Valery, here it comes:

Well you know how to solve it numerically, using Odesolve.
I give you the symbolic solution:


An example with F= -1, n=sqrt(2):

To find the asymptote:
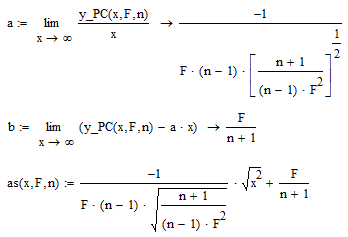
Regards,
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you.
I think it's a great honour to be named second in place after Christiaan Huygens.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Thank you.
I think it's a great honour to be named second in place after Christiaan Huygens.
Luc
About it in my article - http://twt.mpei.ac.ru/ochkov/Mirror-Lens-macket.pdf

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And what is the formula for y(x, F, n) at the case not n=sin a/sin b - for n=a/b?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is this a physical reality?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Is this a physical reality?
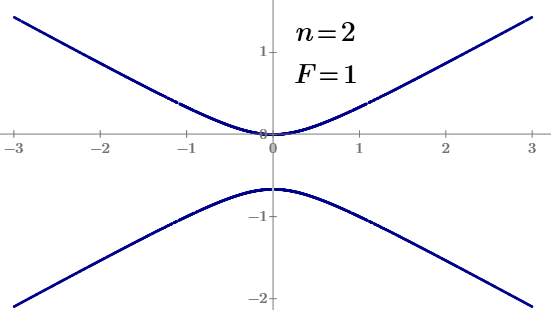
At little angles! See plots avove!
This is a solution of one DE!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc
Could you post the worksheet for that?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I join the request too.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Rich,
Here you are.
It's Mathcad 11. I suspect some things will not work in other versions.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks.
You are correct. A lot of the symbolic stuff does not work with the Mupad engine. If I find the time I'll see if I can fix it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
From my future article - sorry - Google translation:
We used two methods for solving optical problems - numerically using Mathcad-function Odesolve and analytical through the site wolfralpha.com. But there is a third (crafty and lazy) way of solving such problems. You can place a problem on the site PTC Community/Mathcad and wait for it someone decides. Thus it was obtained "terrible" formula for y1s (x), placed in the center of the figure 7. It is calculated profile of the focusing lens without changing their angles of the sinuses. This formula (complex analytic solution of a differential equation) led one user Mathcad from Holland - the birthplace of the great Christian Huygens, who made a great contribution to the development of optics - see. https://community.ptc.com/t5/PTC-Mathcad/asymptote-odesolve/td-p/183281. This user Mathcad (Luc Meekes) was the good old 11th version of the engine with a character from the Maple, and not from the MuPAD, which made it possible to solve the problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
The result of the calculation in Mathcad 15 M045 version you can see in the attached PDF file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks.
You can surely understand how happy I am with Mathcad 11.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Thanks.
You can surely understand how happy I am with Mathcad 11.
Luc
You can surely understand how happy I am with... Luc and his Mathcad 11. ![]()
Val
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One partial case of the Luk's formula ( from one Russian optic hand book - https://mipt.ru/dasr/upload/89a/f_3kf3p7-arphh81ii9w.pdf )
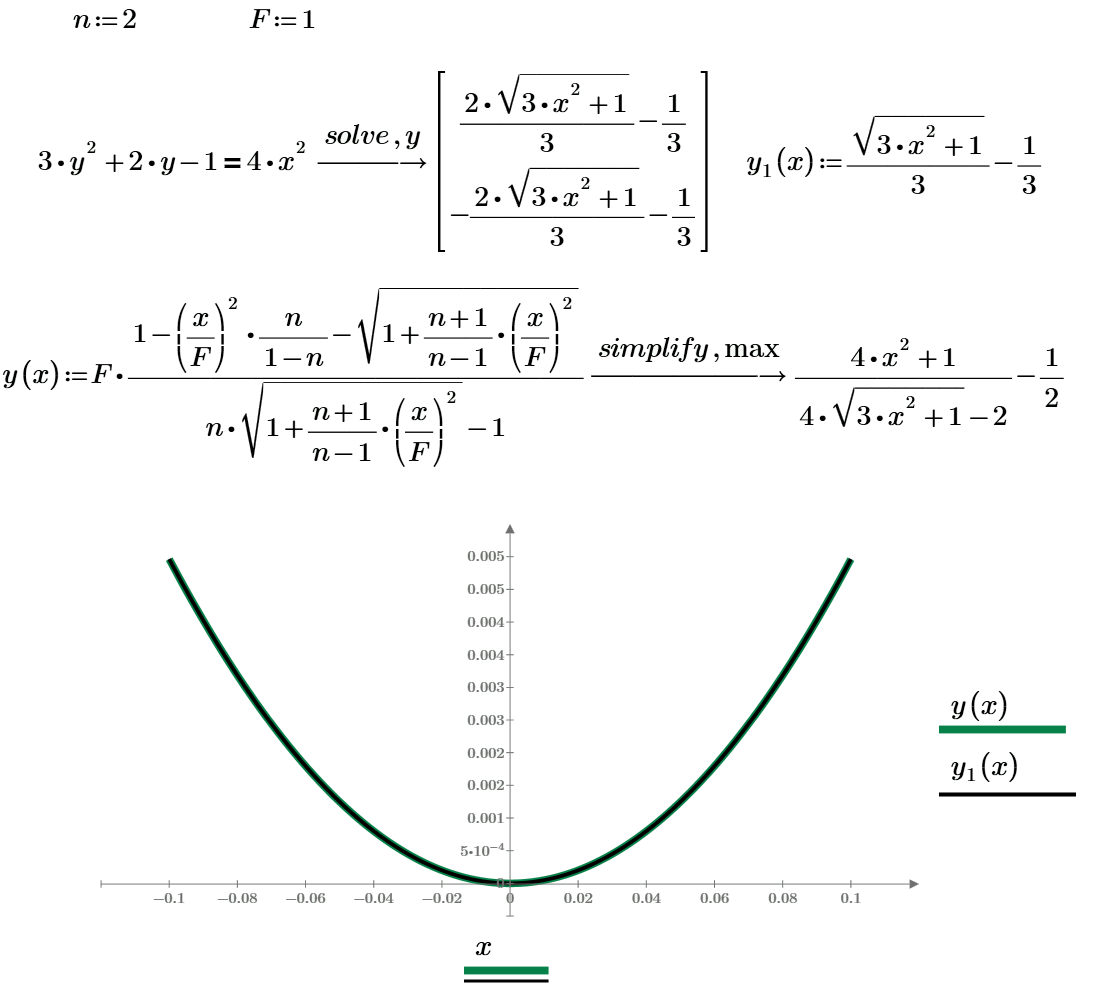
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more solution thru a tautochronism
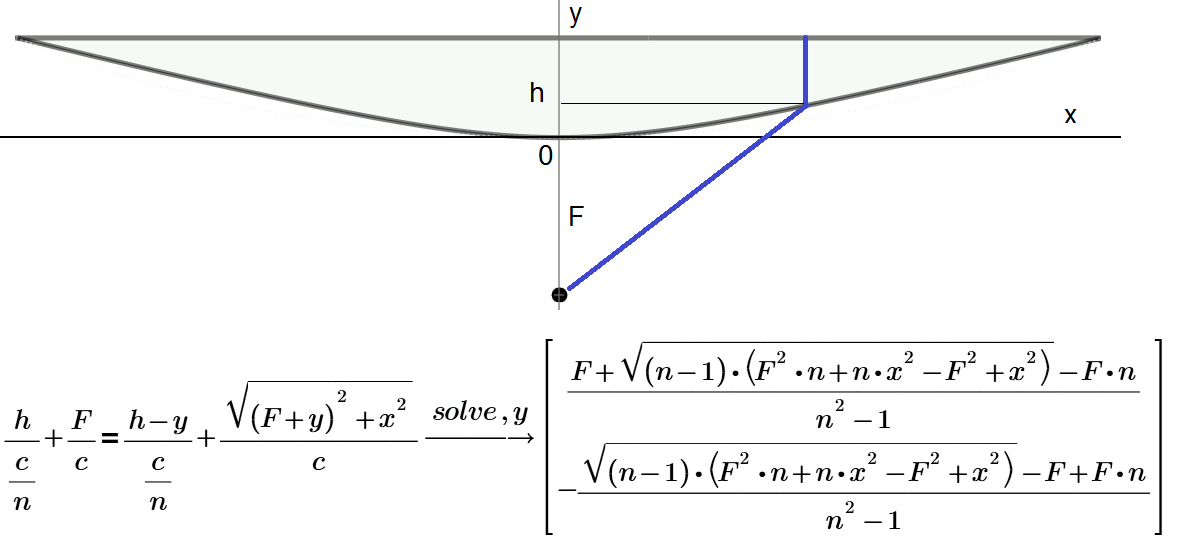
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great, Valery!

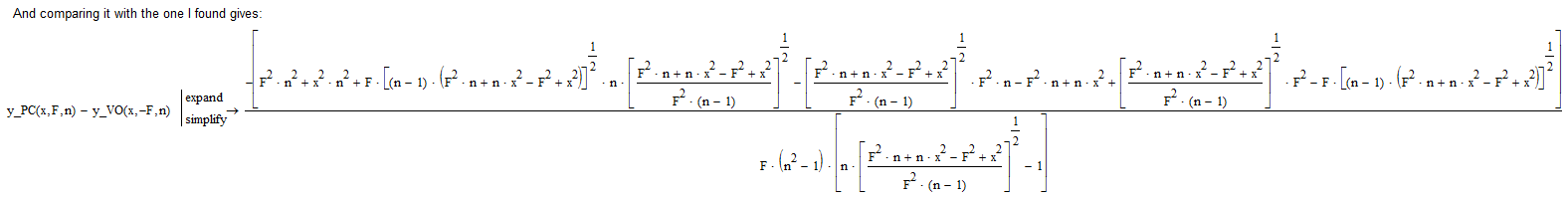
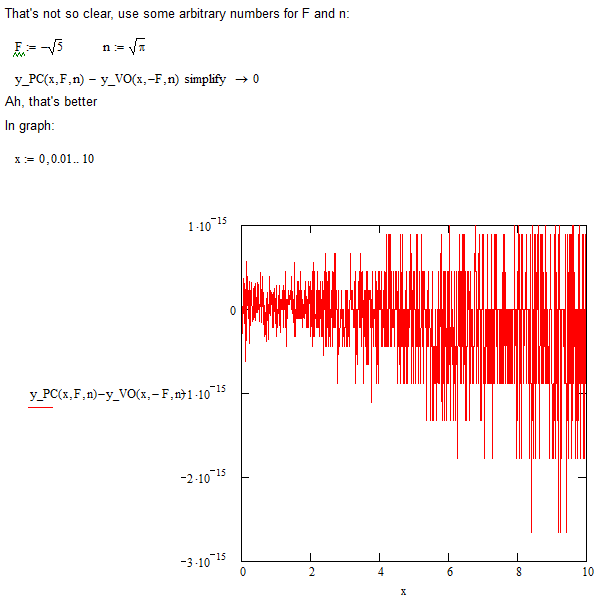
I am convinced.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
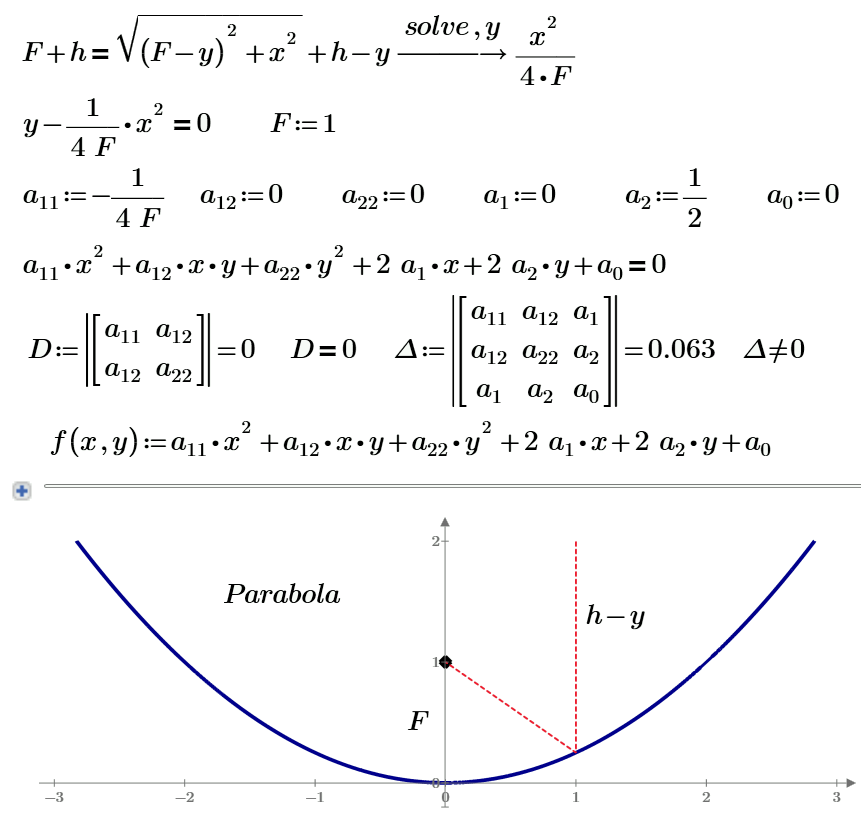
I think it is an errror of numrerical calculation.
The question is.
Is it a one branch of a hyperbola?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ValeryOchkov написал(а):
I think it is an errror of numrerical calculation.
The question is.
Is it a one branch of a hyperbola?
Yes, hyperbola! One question - why not simplify h*n=h*n

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is any physical in second branch of the hyperbola?
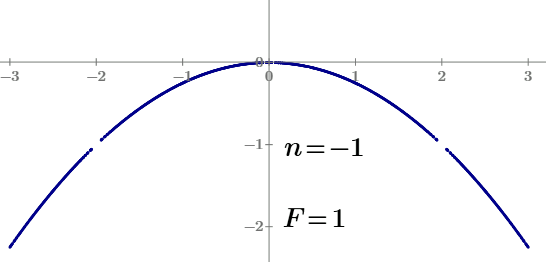
A parabola
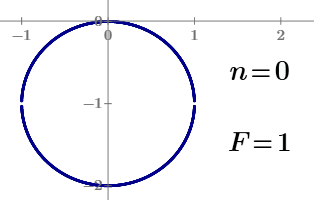
A circle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One simple example

But how can we show that two function y_PC and y_VO are equal? Like sin and tan*cos.