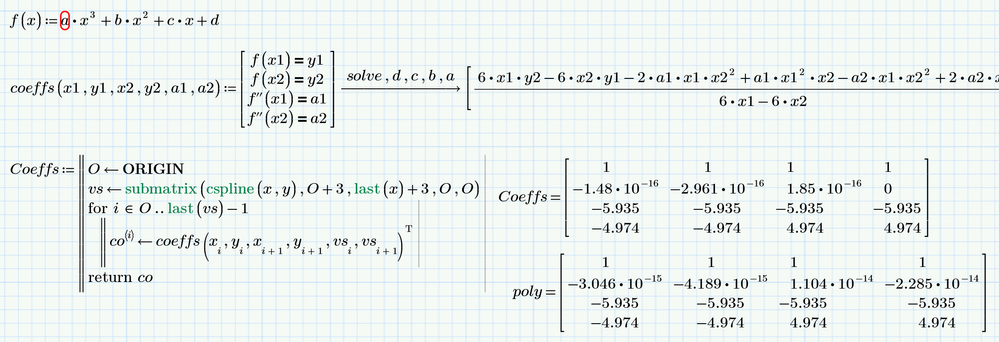Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
cspline
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
cspline
Has somebody Mathcad sheet which return coefficient a, b, c and d of the equations y=a*x^3+b*x^2+c*x+d of the cspline?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the good old Mathsoft days we were offered "The Mathcad Treasury" and there Paul Lorczak shed some light on the meaning of the vector produced by "cspline". Unfortunately at the time I have no access to the Treasury but as a long time Mathcad user you probably have it lying (3 1/2 " disks !!) around in a drawer. Find it and look up "Computational insights_Think before you spline" or maybe "Cubic splines and alternative curve fitting techniques" - not sure.
Chances are that you will find the information, you are looking for, right there.
According to the Mathcad documentation (yes folks, there were times when Mathcad would come with a good solid user guide and complete reference) the vector created by cspline contains, among other things, the second derivatives for the spline curve(s).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
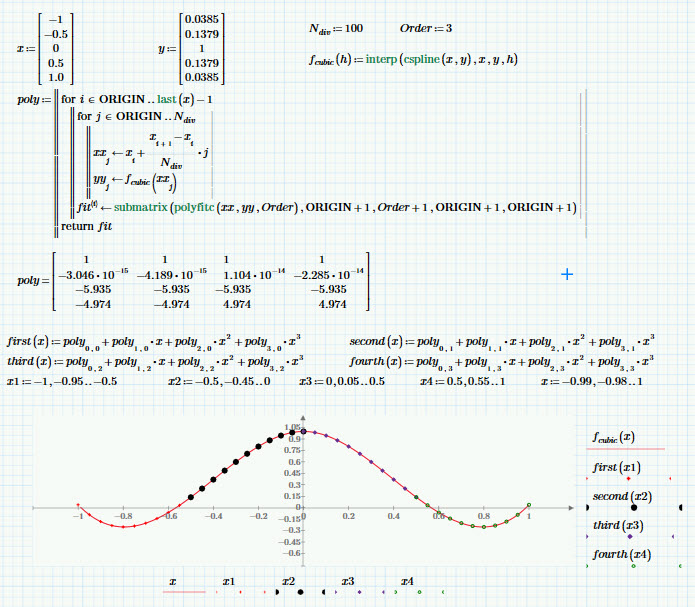
You'll consider this cheating, but we can work backwards from the spline mathcad produces. Probably not what you want, but you do get the coefficients. Here - I let MC do the fit, take 100 points along each segment and create a fit for each segment. Seems to work. Attached is the file, along with another that seems to imitate lspline quite well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@DJF wrote:
You'll consider this cheating, but we can work backwards from the spline mathcad produces.
Its sure cheating, but its a very clever cheat 😉
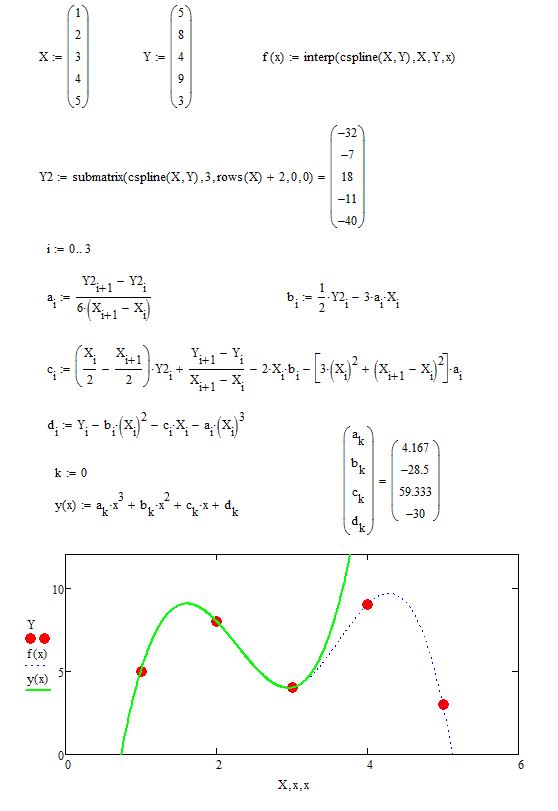
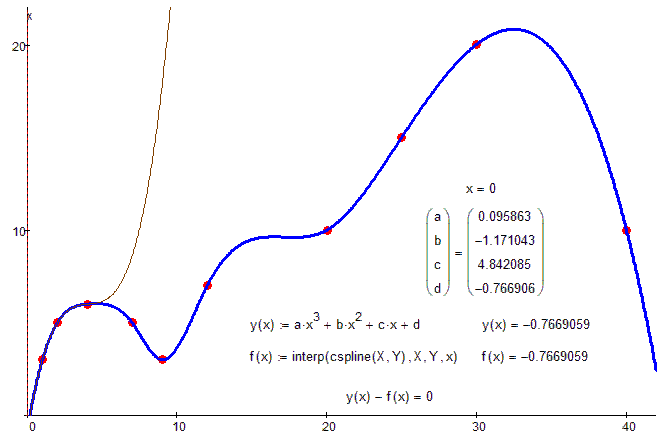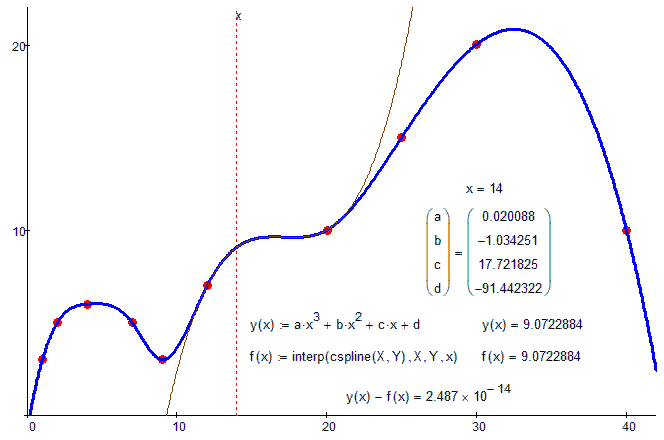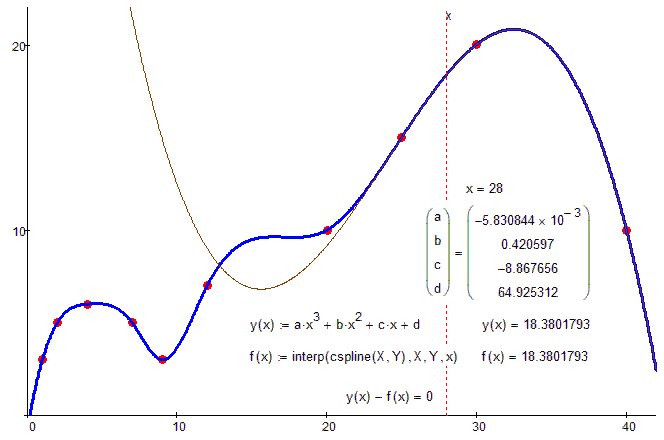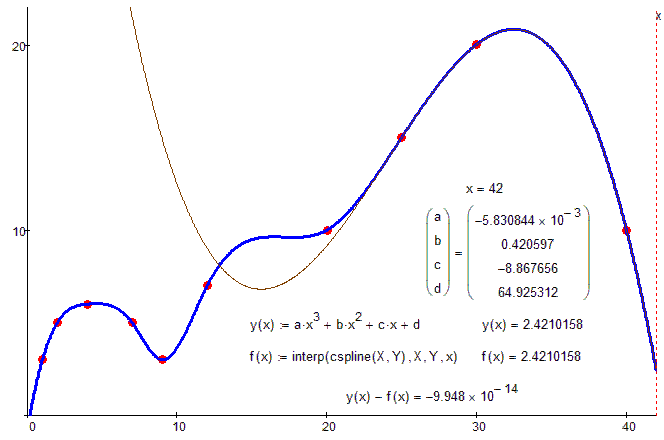
After playing around with your sheet and knowing that the vector created by cspline contains the second derivatives, it was quite easy to derive the coefficients directly from that vector:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a non-cheating version (i.e. never using cspline). Bit crude but seems to work. See:
https://www.researchgate.net/publication/236029592_Cubic_spline_interpolation_using_Mathcad
for a good paper on how cspline, pspline and lspline work.
4.0 and pdf attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have this version.
- Tags:
- mathcad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Valery!
But solution without animation is not solution!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One picture for more understanding: 4 equations with 4 unknown (coefficients a, b, c and).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or so! Like ODE but not ODE