Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
finding ANY point inside a printed shape
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
finding ANY point inside a printed shape
Hi a friend's just asked how you find ANY point inside a printed shape without testing mountains of points.
I suggested the simplex method with a dummy objective function but all the trivial examples I've seen consist of (in themselves) unconstrained straight lines that interfere only at suitably appropriate points .e.g to form a nice convenient triangle.
I've attached a diagram of the "feasible" region and as you can see if you continued some of the implied lines forming the edges you'd slice the region to shreds.
My question is how would you represent the truncations of the lines in your system of inequalities.
BTW Assume you're talking to a layman...'cos you ARE! <smile>.
Thank you in anticipation for any forthcoming help.
Dean
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No algorithm in particular i.e. LP was the only one I was aware of that got you a point on the enclosed region. What we're after is ABSOLUTELY ANY x,y point INSIDE the arrow i.e. not on the boundary/lines. My friend said he doesn't want to try lot's of points out so I was looking for a calculated method to get on the boundary. From here it's a question of testing the movement of the point in 8 directions until you find one that moves the point inside the boundary/line. That's all really i.e. no real optimisation as such, just enough to get a feasible solution. I don't know if there's an easier algo to do this?
Again thanks for confirming that line segments/coordinates is our best bet.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure what kind of MATHCAD help you would need and in as much this would have to deal with "Statistics & Data Analysis". I would suggest to attach the Mathcad sheet with your problem to show what version you use, what you have done so far and show what you are after.
I've attached a diagram of the "feasible" region and as you can see if you continued some of the implied lines forming the edges you'd slice the region to shreds.
I am not sure what you mean by this and I have no idea what the starting point of your problem would be - a scanned picture, an area given as polygon, ... and also its unclear to me what the endresult should be - a function which decides if a point is in or out, a list of "all" points inside an area, a plot of all points inside the area colored in a distinct color,....
You would first have to state whether we are dealing with vector or pixel graphics (your attachment suggests the latter) and how the boundery of your are will be given.
Generally there are some quite proven and efficient algorithms available, maybe the wellknown, widespread and easy to implement "floodfill" algorithm is what you are looking for.
My question is how would you represent the truncations of the lines in your system of inequalities.
Huuh!?? ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Thank you for your response and for "floodfill".
I have no solution because I don't know how to specify the system of inequalities or even if they are specifiable.
That is my question.
LP finds the optimum solution on the boundary of a region constructed by intersecting lines.
The attached diagram shows two pictures.
One is the typical y=mx+c lines that are not constrained re their extents and typically form a nice convenient triangular region from which you find your solution.
Re the diagram in the first post...the 2nd picture underneath the triangle shows that if that pixel diagram converted to vectors of the same form i.e. y=mx+c.
You can see that in thelr unconstrained form these lines slice up the drawn arrow/region so I'm not sure if or how LP can cope with such a region.
An optimal solution is not required i.e. any point on the boundary of the arrow will do...it's just that LP is the only method I know that takes a system of lines and gives you a point somewhere on the boundary.
if we take the top of the arrow...it's a 4 pixel horizontal line and assuming it was drawn at the top of the screen we could represent it as y=0 but only for x>18 and x<23. Unfortunately, other lines require x to be limited to other values so I can't see how you could rope x into your system so as to limit the length of your lines.
Does that make things any clearer?
BTW I'm not seeing a link to add attachments like I did in the first post
Edit...Ahh you have to post and then Edit and then the Attachment facility is visible.
gary3.png is crude but shows what happens to the arrow region when you don't constrain the extent of the lines that form it's boundary.
This doesn't happen with problems in LP tutorials e.g. like the triangle (shown).
Can LP handle regions shaped like this arrow?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What exactly do you mean by "find any point inside a printed shape"? It's not clear to me what it is you want to do.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
High a pc screen is simply an array of pixels with x and y co-ordinates just like a piece of graph paper or spreadsheet.
see diagram in first post.
If you wanted to you could draw the pixels around the edges of the arrow shown as a series of lines
e.g. above I gave the equations for the very top of the arrow (which represents one of the edges).
All that is required is literally ANY point (x,y) that lies on the arrow shown.
The problem is in most example LP problems the lines can be as long as you like and will never cut through the triangular region.
By contrast if you lengthen or shorten the lines that make up the outer edges of the arrow....you compromise the region.
This is where I'm struggling with LP as a potential solution so...
I'm look for a way of calculating a value for x and y given the equations of the lines that represent the ouline of the arrow
i.e. as if it's a feasible region
that will guarantee a hit inside the arrow's area.
Quite where inside is irrelevant cos this is not a real optimization problem...
i.e. it's just that LP generally forms the region from multiple lines for you.
Hope this helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't understand why you insist to solve a discrete problem using continuous analytic methods.
Anyway - you are searching a solution using Mathcad, otherwise you wouldn't post the question here. You have to provide a worksheet for further help. You say, that you don't have a solution - thats obvious, otherwise you wouldn't havbe to ask. But you must have at least soemthing to start with in Mathcad.
Its absolutely unclear to me what you want to do and what your startin and endpoint should.
So forget about describing the method which you think would solve your problem and rather descrive the problem itself!
Whats the starting point? A set of equations and inequalities? A scanned pixel graphic in a specified coordinate system? Whatever it is, provide a sheet containing it.
Whats the goal, the end point? A function with two arguments (coodinates) which determines if a given point is inside a shape (what shape?) A n x 2 matrix of the coordinates of all blue pixels in the picture provided? Another pixel graphic?
You have to specify the problem before we can talk about the method to solve it.
It may also help if you tell us where this problem stems from - whats the reason for aving to "find any point inside a printed shape" (whatever that may mean).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't understand why you insist to solve a discrete problem using continuous analytic methods
That's because I don't know any discrete methods
Whats the starting point?
Whats the goal, the end point?
l believe I have explained that the starting point is a set of linear equations for the lines that bound the arrow shown. I also believe I have explained that the end point is a tuple x,y (Indeed any tuple) that lies within the region represented by the lines for which the equations are given.
You have to specify the problem
Haven't I explained that I'm struggling to do this because I'm not sure how you constrain the length of the lines i.e. the very top edge of the line is y=0 but only for 18<x<23.
By contrast the top edge of the arrow's shaft is y=1 (y increases as you go down a pc screen) but only for -1<x<18.
i.e. I don't see how to represent the system when x varies so much.
In all of the LP examples I've seen the lines are not restricted in their length ie. they're just y=mx+c without any further restriction so LP might not be the thing.
Give me a minute and I'll enhance the diagram
Ok here are two diagrams
In the tutorial LP problem the lines lengths have no bearing on the feasible region so you just specify the lines as y=mx+c.
By contrast if you look at the cyan lines forming the arrow for which I'm sure you can imagine their equations
particularly as I have given two of their equations above
...their extents (and not just their equations) affect the shape of the region
and I'm not sure how you specify these.
This uncertainty re specification IS my question
so asking me to specify the problem is akin to asking me to anwer my own question?
Just added gary5.png
Forget the equation of the single cyan line shown (top of arrow shaft)...see what happens to the region formed by the previous lines when that line is extended i.e. it alters the region whereas in typical LP tutorial problems this doesn't happen. Thats my problem...how would you represent limiting this line's extent and the other ones when each time you do you contradict potentially break the limit you set for the previous line
e.g. in my example above the top of the arrow requires 18<x<23 but the shaft requires 0<x<23 i.e. to contain the shaft line y=1.
This is completely contradictory to my mind so I'm unsure how you represent it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have to accept that you insist to specify the method you think is appropriate and are not willing or not able to describe the problem itself.
You claim that the starting point would be a set of equations, but all you provide is a pixel graphic.
I fear I can't be of any help that way.
Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
>but all you provide is a pixel graphic.
Untrue...
I supplied a pixel graphic with all bounding lines drawn on and the equations for two FULLY described, the rest being pro-rata and obvious to any one undertaking o-level maths I'd have thought. Here the lines you deny...
y=0 where 18<x<23
y=1 where -1<x<18.
In light of these equations your uncertainty re whether I am unwilling or unable to precisely specify the problem seems strange unless of course you can explain how, in a system of linear inequalities, x can be both limited to between 18and23 and simultaneously to between -1and18.
If you can explain this then you've answered my question and if you can't then it will show why further elaboration is difficult.
Either way your response will be helpful so please...respond.
We're talking about mathematical representation here which I don't think a mathcad worksheet can help with.
Can the above lines be part of the same system of linear inequalities or not
given that the limits for x need to be expressed and are seemingly contradictory.
I've not encountered this before and don't know how to deal with it.
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
the starting point is a set of linear equations for the lines that bound the arrow shown.
A set of linear equations for lines do not necessarily define a unique shape. Given the red lines, either the black shape or the green shape (or other shapes) is possible:
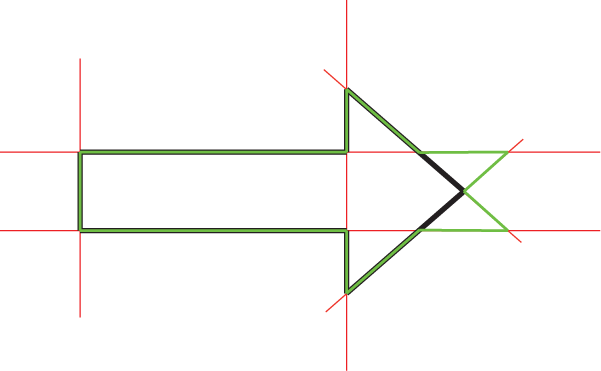
A polygon is usually defined by an ordered set of coordinates of the vertices.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bless you Richard
That's the problem exactly...with not being able to limit the length of the lines.
In all of the tutorials I've ever seen the lines never cut like that irrespective of how long they get.
This arrow is the first time I've encountered this and threw me.
I'm not sure how or if we can get vertices.
Leave it with me and thank you for very much for your advice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have to treat it as a sequence of line segments, as shown in gary4.png (i.e. 21 consecutive line segments), or equivalently a sequence of coordinates. I can't really say any more than that because I don't know exactly what algorithm you are trying to use.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No algorithm in particular i.e. LP was the only one I was aware of that got you a point on the enclosed region. What we're after is ABSOLUTELY ANY x,y point INSIDE the arrow i.e. not on the boundary/lines. My friend said he doesn't want to try lot's of points out so I was looking for a calculated method to get on the boundary. From here it's a question of testing the movement of the point in 8 directions until you find one that moves the point inside the boundary/line. That's all really i.e. no real optimisation as such, just enough to get a feasible solution. I don't know if there's an easier algo to do this?
Again thanks for confirming that line segments/coordinates is our best bet.





