Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
finding number of maxima of a noisy signal
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
finding number of maxima of a noisy signal
Hello everyone,
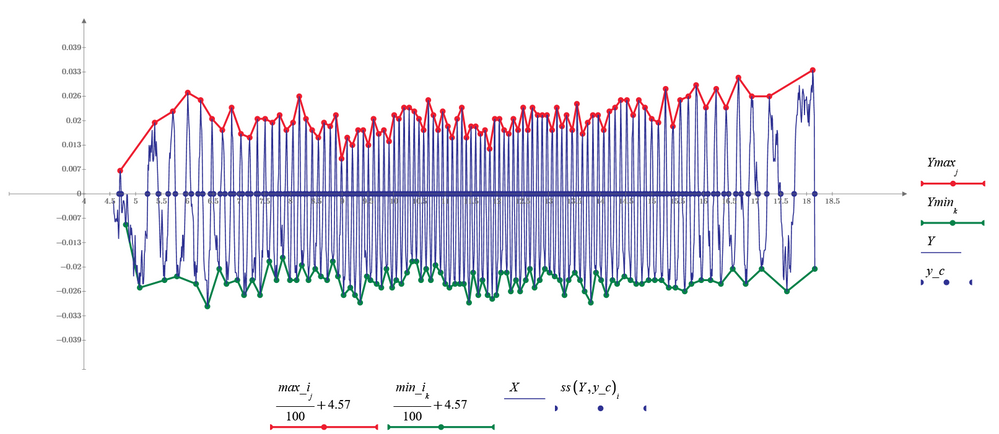
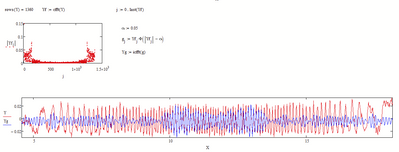
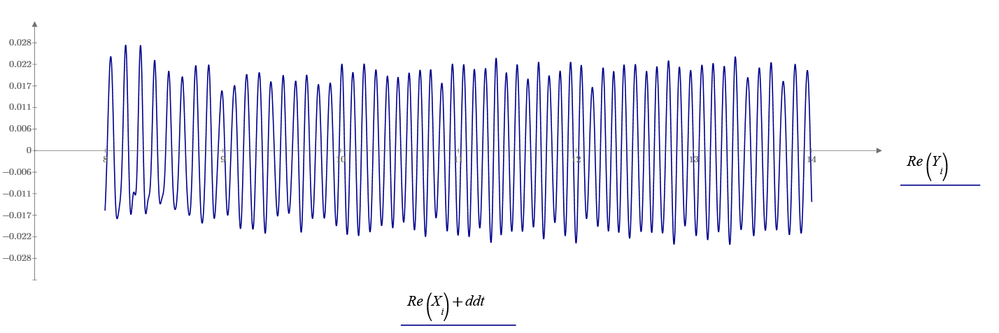
In the attached worksheet, I would like to find the number of maxima of a noisy signal.
I have observed that the built-in "localmax" function, misses some of the peaks and considers some false peaks even with the window option that could be hard to use with higher frequency signals.
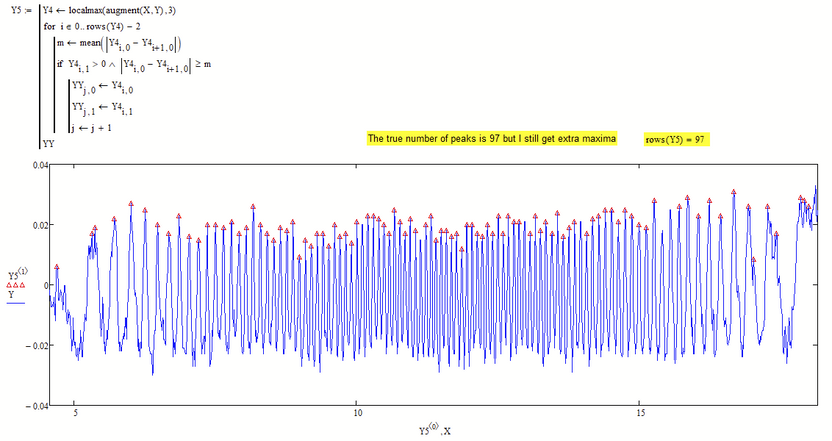
To develop the algorithm, I have smoothed my signal using "movavg" and "loess" functions and finally set some conditions to disregard some of the false peaks. However, there is still a difference between the true and extracted number of maxima. In the current worksheet, the true number of maxima in the attached file can be counted 97 but I have got the number 101 so far.
I appreciate it if you share your idea and advice on this worksheet.
All the best,
Payman.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe not using the fitted but rather the original data and using the optional window parameter of localmax will help (of course "augment(X,Y)" could be replaced simply by "data")
BTW, to save large data in a Mathcad worksheet its better to use Menu "Insert"-"Data"-"Table" (see attached sheet)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Werner.
The point here is that although the total number is correct, some of the true peaks are missed, and instead, some false peaks are counted. I have observed that by using this approach for higher frequency signals, many true peaks will be missed which must be double-checked manually. I am wondering if a more reliable approach could be worked out.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I noticed that some peaks are missing while some extra peaks were added in-between.
The problem is how one exactly would like to define a "peak" so it can be programmed or some out-of-the-box tool can be used. A human probably could see at first glance where a peak could be assumed and were not, but its sure hard to define it in a more general way so a machine can make the same decision.
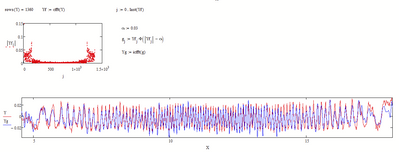
Not really sure but depending on the signal a fft may be of help?
Or how about a larger span value in loess (e.g. 0.01 instead of 0.005)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is there a reason why your data varies in frequency over the sample? The ends cycle very slowly compared to the data at the center of the time interval.
I had originally thought that Fourier analysis (fft) might be useful (a low-pass filter to screen out high frequency noise) but the frequency shift in the data may make that challenging.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it doesn't look that fft would be of much help here
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
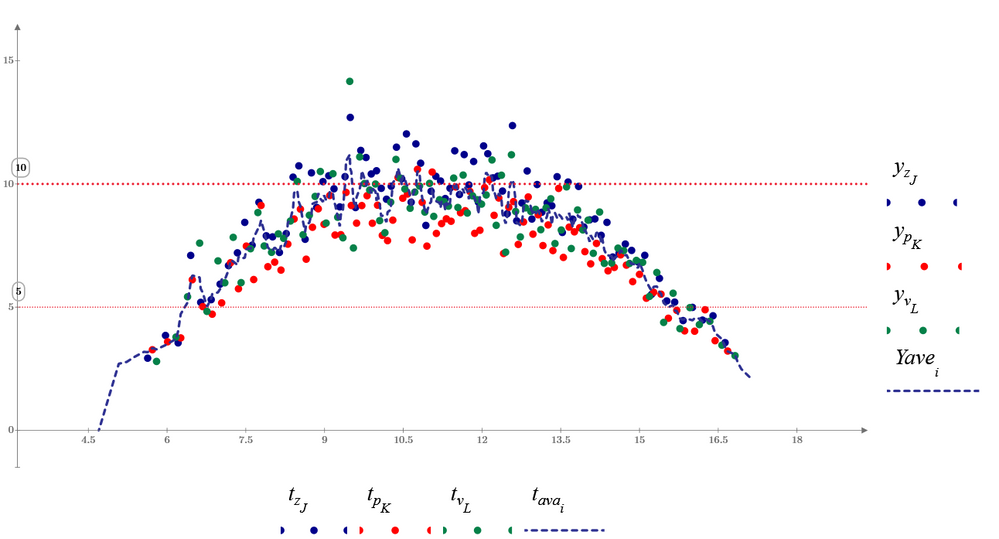
This is the laser interferometry data of an oscillating object. The peaks show the number of times the object traveled half-wavelength distance. When the object reaches the end of its course, the velocity is zero and hence we observe a zero slope area at the very ends of the plot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"The peaks show the number of times the object traveled half-wavelength distance. When the object reaches the end of its course, the velocity is zero and hence we observe a zero slope area at the very ends of the plot."
So we could treat this as a frequency modulated signal--the frequency is modulated by the speed of the oscillating object. The number of half-wave peaks correlates to the amplitude of oscillation.
Window your raw data into short overlapping segments, say 5 msec long with a 2 msec overlap. Take the fft of each segment, plot the largest amplitude frequency for each segment. That frequency times the width of the window should be the number of half-wave peaks in that segment. Some thoughtful fudging may be required.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think Werner addressed the core issue: what do you define as a local maxima? For the data sequence 1,2,3,4,6,5,6,7,8,7,6,5,4..., does this have one local maximum (8) or two (first6, 8)? Do you want the maxima identified based on samples, or some filtered/reconstructed version?
You mention "true" peaks and "false peaks" in you original post, with some distinction between these and the extracted peaks. To me, this implies that you have some well-defined test which identifies "true" peaks, which is somewhat different from the analysis you implemented.
Can you post the file/data in a v11 format?
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lou,
By the false peaks, I meant the wiggles around a peak that the program identifies as a separate cycle.
I have attached the v-11 format.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
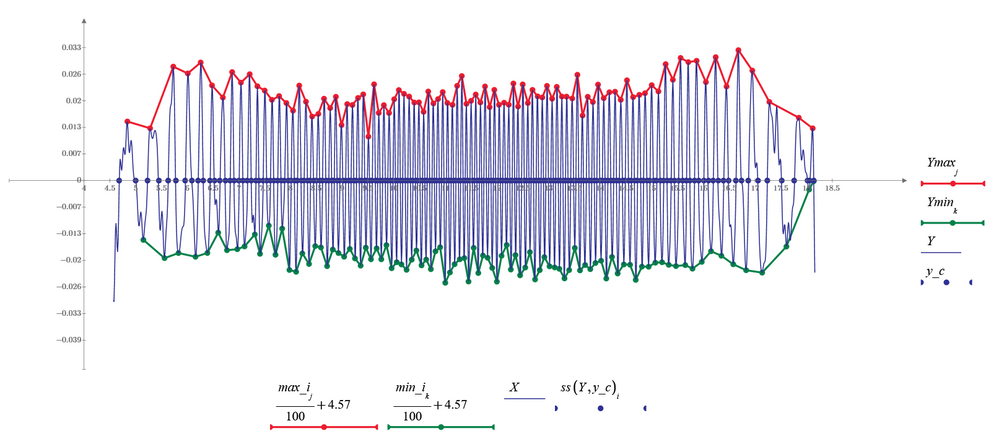
I just had a look at the way you calculate Y5 and wondered what you had in mind with the highlighted parts.
Basically you take the mean of one single value (which is just this value) and ask in the next line if this value is greater or equal to itself (and of course it always is ;-).
Basically your calculation just eliminates the peaks with a negative y-coordinate.
The outline of an algorithm which may work could be as follows:
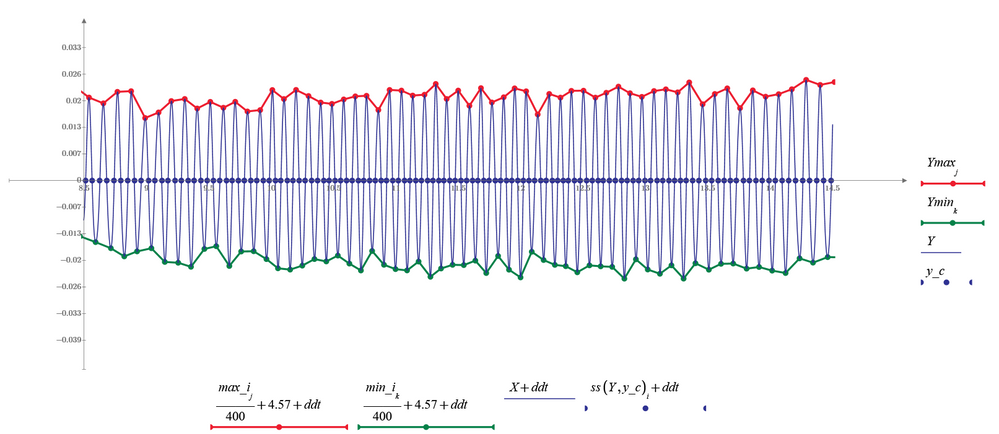
Calculate the local mins as well. A max is only accepted as a peak if the min between it the preceding peak is lower than a certain threshold you would have to define or of the difference of the y-coordinates of the min and the max is greater than a threshold.
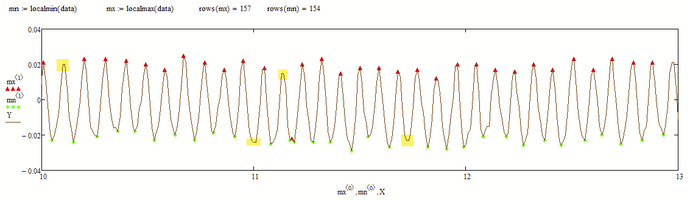
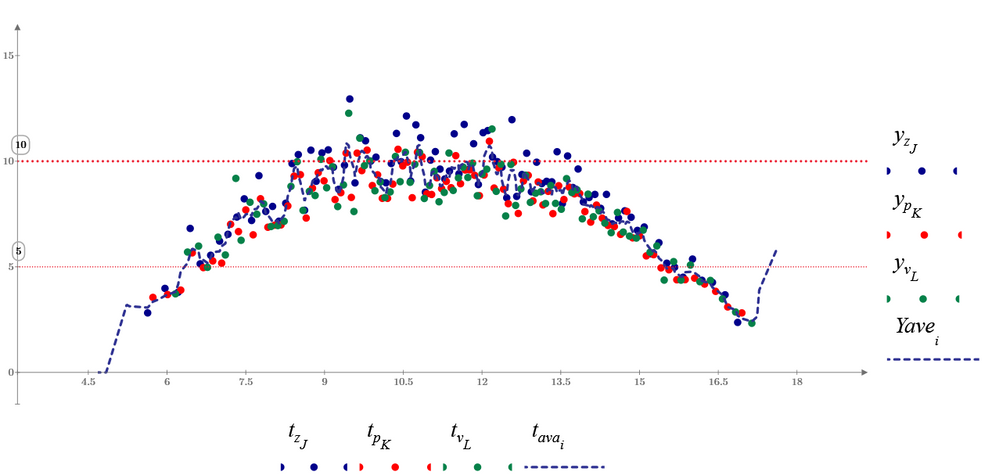
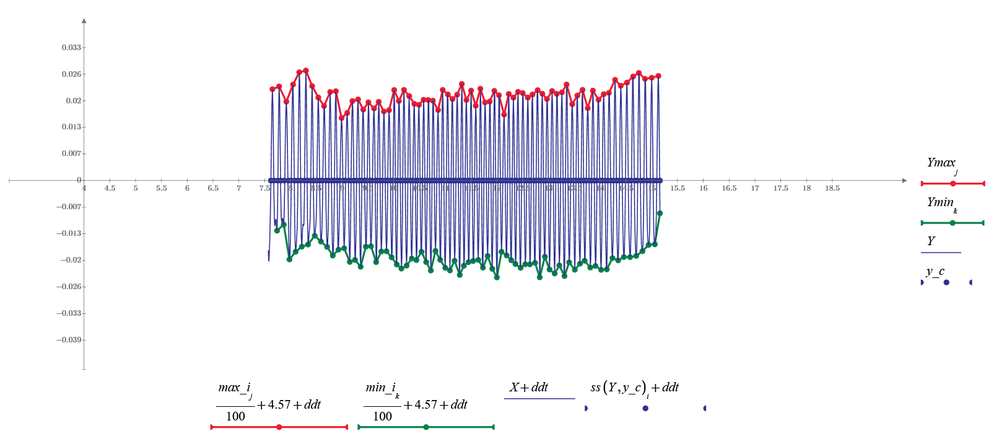
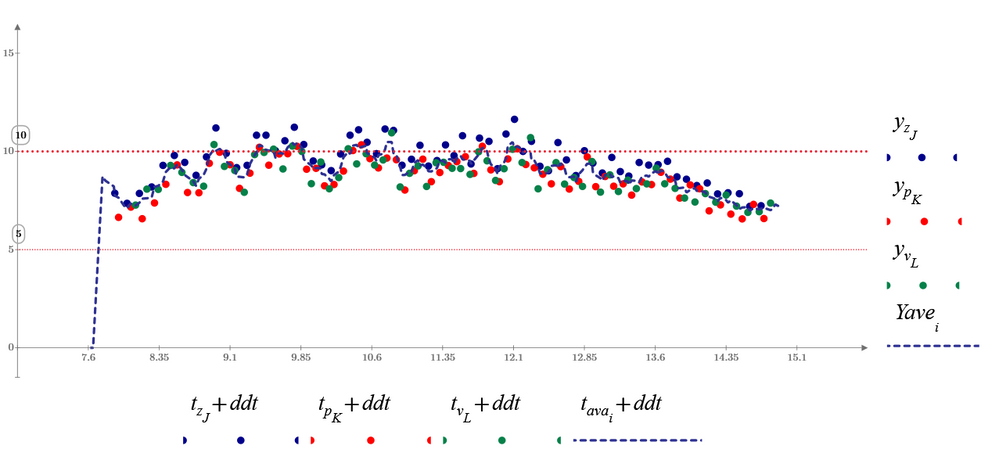
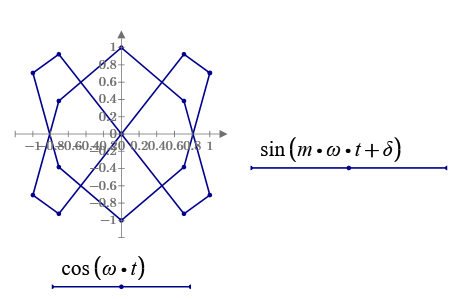
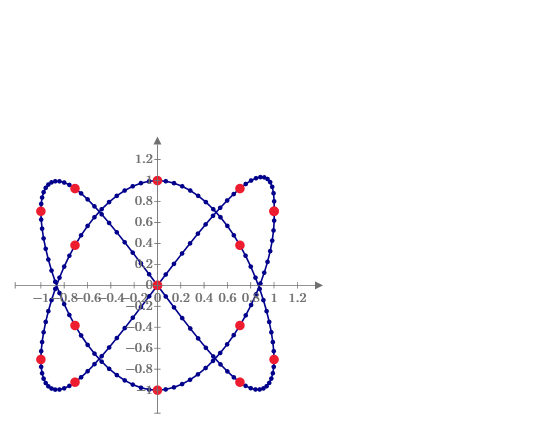
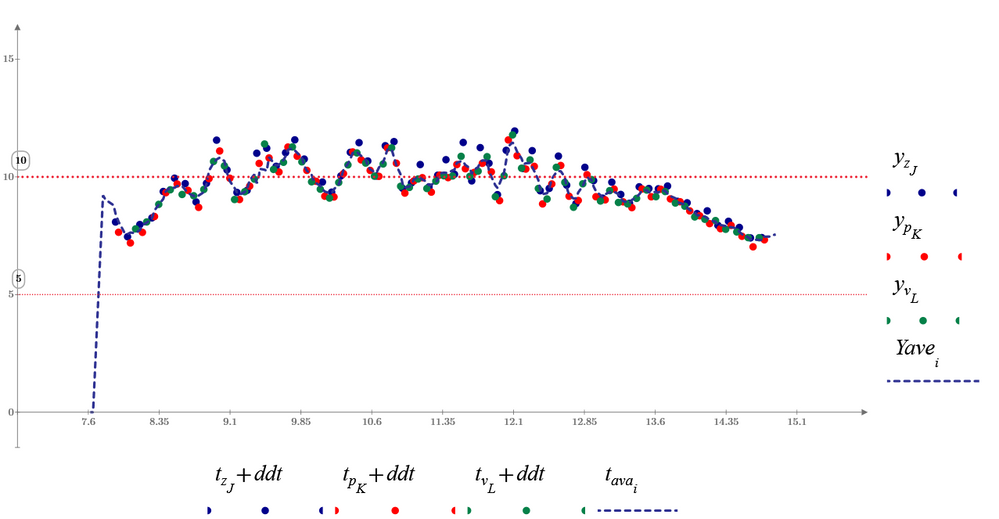
The actual implementation can certainly be made more difficult by a few details. For example, it must be ensured that the minima and maxima interweave perfectly, i.e. there is always exactly one minimum between two maxima, etc. I tried briefly to get an overview and determined the extreme points directly from the raw data. Unfortunately "localmax" does not recognize some maxima if neighboring points have the same (or too similar?) Y-coordinates. See image. So you probably have to work with a smoothed or interpolated signal after all.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
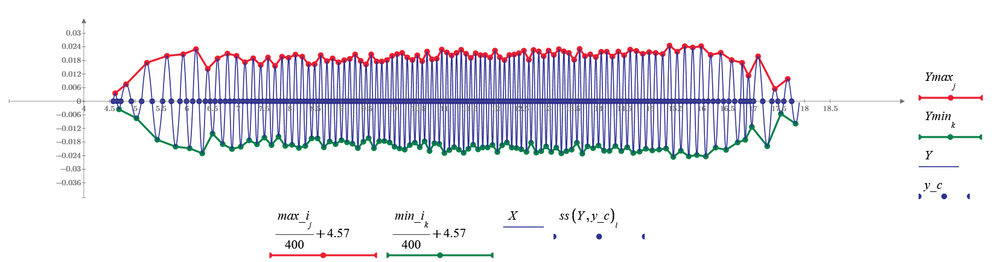
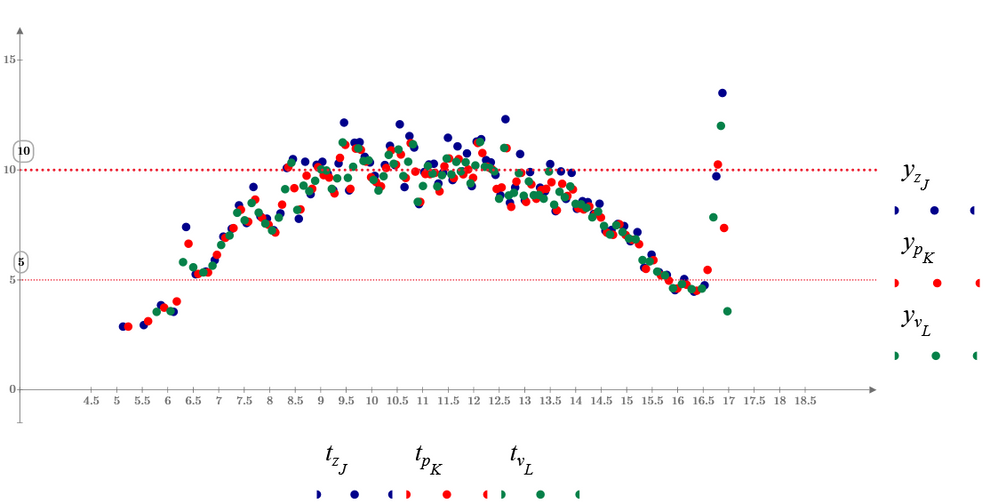
Using Werner_E's many hints, this sheet can find local maximum and minimum more accurately.
- Tags:
- electric circuit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot.
Unfortunately, I am not able to open the file. Could you please try again or change the format?
Payman.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is great. Can you convert the file to Prime 4 or Mathcad-15?
Thanks again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attached is the worksheet copied to Prime 4.0 (Express), less all the pretty graphs.
Express cannot execute the programs--hope it works for you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much, Fred.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fundamental signal only.
- Tags:
- Electric_circuit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Band pass filter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Local band pass filter.
- Tags:
- Electric_circuit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Local band pass filter with over sampling.
- Tags:
- Electric_circuit