Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
graph curve manipulation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
graph curve manipulation
Hi All,
I am trying to get a skewed bell curve to represent a chemical in a reaction via an equation. This first bell curve will be subtracted from another skewed bell curve that represents a second chemical in the reaction. I have tried many equation types and have settled on the one that I am currently using. The trouble is that I cannot manipulate the equation variables enough to attain the configuration that is needed.
Would you all inspect my equation and advise me on whether it can be edited to fit the Benchmark dots on the graph. Maybe another variable can be inserted into the equation? If, not, can you recommend a new equation? The curve slopes are not as critically important as the start, finish, and peak positions and values.
As of now, the starting(blue) and finishing(cyan) points are good. It is the peak(green) that must move to the right without sacrificing the other positions.
All help is very appreciated.
Thank you,
Gary
Mathcad 11
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
I just saw this Reply after I replied to your other Reply. This looks GREAT! I can't wait to try it. I didn't know that sin would work. I guess I was wrong.
You and Werner Exinger know your stuff. This just multiplies my previous Reply to you regarding posting what you asked for originally. I hope I have learned my lesson. Even though I did think that I was doing the right thing, I will try to follow your leads next time.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc and All,
I just produced it and it works as it is written. I don't know how to translate this into php internet coding as it has parts that might not work in php. I would not know how to php code the X and Y stacks and I don't know how these are even part of a mathematical equation. Are the stacks a mathcad shortcut only? I am not advanced enough to know this. Are you familiar with php coding and if so will this translate to it?
This seems to be a great answer in the mathcad realm but can it work in the non-mathcad world? I hope so.
Until I learn how to parse this I am relegated to the equation that I posted.
Thank you again for a great Reply but as of now I don't know how to use it. I hope you or someone can show me. In the mean time I will study this.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think (though I have no experience with php coding) that coding in any programming language (including php) should not be a problem.
You don't need the vectors per sé. You can use variables X0=29, X1=173...Y2=0 instead.
The constructs like (X0<x<X1 you can replace with the php equivalent of:
IF ((x>X0) AND (x<X1)) THEN ...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh. note that the sine is squared!
If you don't want to square, use trigonometry rules to find that:

Then here you go:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi All,
I acquired a different equation from a file that I received online entitled GUMBEL. I can't recall where I got it. I owe thanks to the unknown author of this file. I manipulated it and came up with a very close result. Here it is.
Thank you All for your assistance.
This should effectively close this thread.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So now, finally, you are providing more points!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Ok, I provided 2 more benchmark points. I always stated that I didn't really care how the two slopes went as long as they were smooth. I still don't have an exact match for the slopes. All I ever really needed were the start, the peak, and the end; 3 benchmark points.
But, I should have relented when you asked for more so I apologize for not putting that out there. And, I thought that by only providing 3 benchmark points, that would free you up from being too restricted. I was caught between the proverbial angel and devil. I should have done it the way that you asked; I must have listened to the devil. I have learned for the next time.
Sincerely,
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Luc for sticking with me. I think I am getting close to understanding this and being able to use it. You have, essentially, two customized equations that intricately mesh with each other. One from X0 to X1 and one from X1 to X2.
I copied the code and have a good working file. I was confused by the ^x and first considered it as exponent x. I later changed it to its literal display.
What is the "^x"? I think it is a boolean "and x"? I wouldn't know how to employ this in an analog equation like this.
What is the ",0"? Is ",0" the fixed point of the cosine?
I don't know how I would php code these two items. I am trying to learn this with internet searches.
I will also experiment with adding two more benchmark points.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc and All,
I believe I figured it out. The "^ x" is "AND x". How does the statement "x > X0 ^ x < X1" work? I understand the "X0 ^ x < X1" part as X0 ^ x will always be less than X1 until it reaches 173. The "x > X0 ^ x" part confuses me as x equals x so x will never be greater than x. Am I figuring this wrong?
The ",0" item represents the ELSE statement.
I believe I can php code this. I still need to understand the "x > X0 ^ x" part.
I tried to insert two more benchmark points and I was not successful. How can this be done?
Thank you very much,
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Gary,
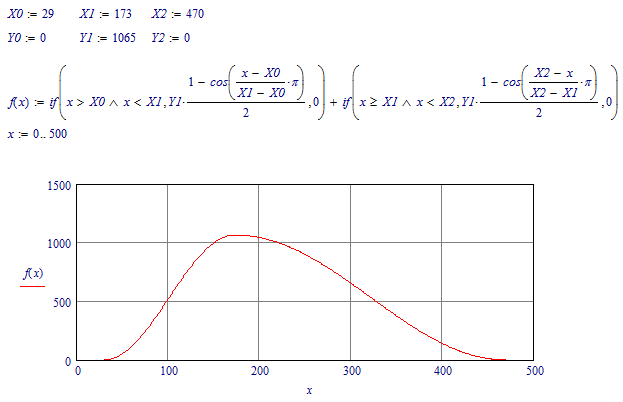
Yes the function consists of two parts, but they are not 'intricately meshed' with each other. They are just two parts, added. The first one is active for x values between X0 and X1, the second one is active between X1 and X2. 'Active' here means, could be other than 0; in the 'inactive' regions their result is just 0.
To get a better match between Mathcad coding and a programming language I have used Mathcad's IF() function, which basically is to be used as:
IF ( {a condition} , {expression when the condition is true} , {expression when the condition is false} )
The condition uses two separate inequalities, x must be larger than X0, so "x>X0", and x must be less than X1, so "x<X1". Both equalities must be true for the condition that I need, so "x>X0 AND x<X1". The mathematical symbol for AND is /\ (not ^), just as the mathematical symbol for OR is \/. You will find both those symbols in the boolean toolbar, because they are boolean operators. In programming languages you will need to use AND (Algol, Pascal) or && (C, C++, C#). I don't know what it is in PHP. Note that, in mathematics, and in most programming languages, the AND (and OR) operators take precedence over the comparisons (<, >, =), just like multiplication takes precedence over addition. So "x>X0 /\ x<X1" is the same as "((x>X0) /\ (x<X1))".
So in short, the function that I defined consists of two parts of a sine squared, or an offset cosine if you will, that are used only for a quarter of their period. The first part between x=X0 and x=X1, the second part between x=X1 and x=X2. For all other values of x, the result must be 0, hence the expression when the condition is false in the IF functions are 0. And since the active regions of the two parts do not overlap, I can just add the two parts.
What I achieved with using these sine squared function parts, is not only that I hit the three benchmark points spot on (because the function actually uses them in its definition). But also that at the benchmark points, the derivative of the function is 0, which makes the parts of the function connect smoothly.
If you add more 'benchmark points' to your input, you are essentially requiring a different function, in that case the gumbel distribution might be a suitable function.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc, Fred, and All,
Yes, I now understand about the "Give these boys all the points you have" mindset. I did not perceive what was going on earlier in the Mathcad realm vs the php realm. Luc has explained this.
There is only one last thing I need to nail this down.. well two things. How do I add another section in the f(x) in order to span between two benchmark points. I have tried a lot of iterations but could not make it work. Please review my file and suggest a fix. How do I represent one of the f(x) equations with a name? This wouldn't work even when I had x = 29 instead of a range of 0 .. 480.
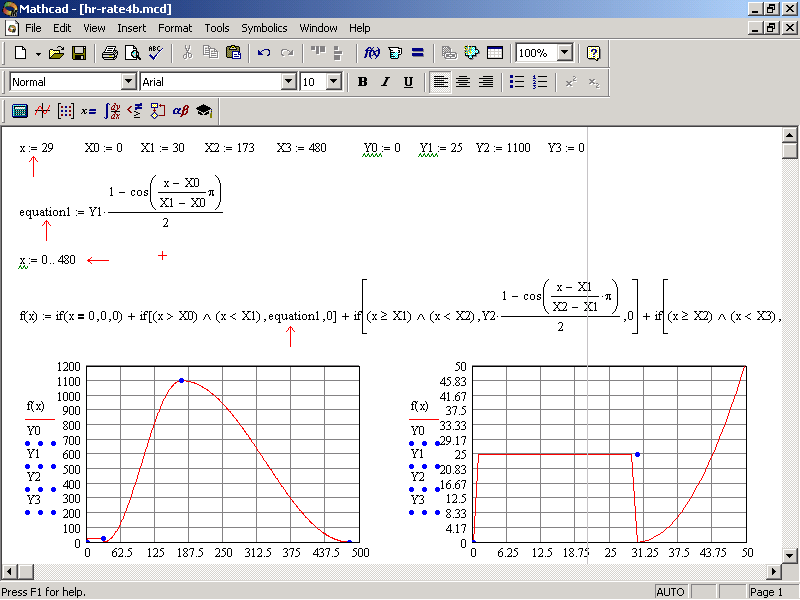
Thank you All,
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached file shows how you would construct the curve with your extra 'benchmark point'. But it has the property, or call it limitation, that where it is non-zero, it follows offset cosine segements.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc and All,
This looks very good but not perfect. There are still glitches. One is where the first part meets the second part. It is not a smooth transition. The second is the first part has a contour that does not lend itself to a smooth transition.
I guess when using more than three benchmarks(start, peak, and end), one must use different equations so the transition points are smooth, although you did not use different equations on each side of the peak, hmmm. I will experiment with this.
I added another benchmark on the right side and edited the equation like you did the previous one. It took me about three tries but I got it.
I can use this arrangement if I have to as the slope is not as important as the three main benchmarks.
I believe that you All have completed showing me how to do this. The final editing is up to me. This was a very fulfilling, engaging and interesting methodology.
Luc, would you choose a Reply and select it as the "Answer" or is that my job or a Moderator's job?
Thank you. I appreciate your extensive help. I learned a lot.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
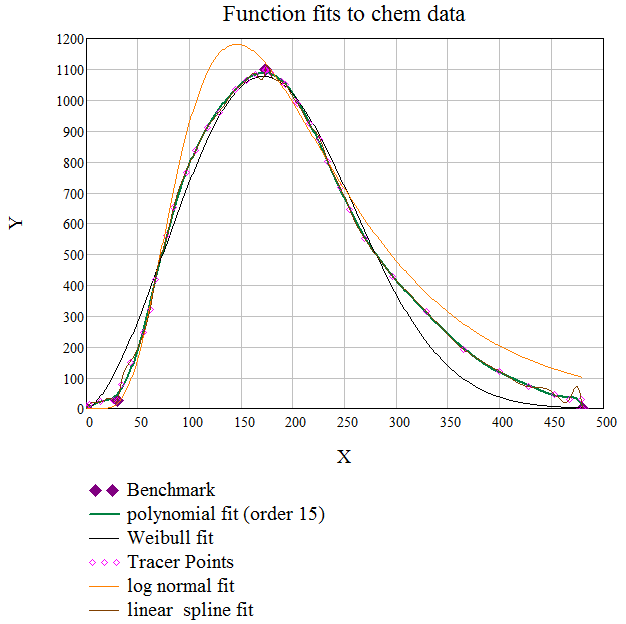
Attached is a fit of various functions to your data. I took your curve (from your original post) and "digitized" it (there is a freeware, "Tracer," that will allow you to click points ad create a data table.) Then I added your three "benchmarks" to that data, and fit a 15th order polynomial, a Weibull function (not the built-in, needed two parameters), a log normal distribution, and finally a linear spline (piecewise) to that database.
A spline fit is an exact match at each :knot." You can see the effects of "hand jitter" in that curve (especially at the right end) as the curve fluctuates wildly over the last four points.
An interesting exercise.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Gary uses Mathcad 11.
Could you repost it as Mathcad 11 .MCD ?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
Please find a Mathcad 11 document in attachment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great work, Fred!
I used your digitized data and fed it in CurveExpert Pro and this program suggests a function type named "Hoerl".
Its a simply function type using only three parameters

I let Mathcad do the job to determine those parameters, but again only the "Optimized Levenberg Marquardt" algorithm would be able to get a result. This algorithm is not available in Mathcad 11, so I provide the values hardcoded in the attached worksheet.
Hoerl does not meet the benchmarks as perfectly as required, I guess. Required for what? Whats the goal? What should the php prog achieve?
Nevertheless, for whatever it may be worth, I added my tries at the end of Freds worksheet and attach the sheet here in Mathcad 11 format.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi All, and thank you All,
Your files would not work, at least as I understand them. I filled in the data fields but variable Y would not be recognized. The first graph filled in but the remaining did not.
The files that were just provided also have a lot of Mathcad shorthand that I would have to learn how to translate into php coding. Luc has already run through this with me in the last file that I posted, chem-rate9.mcd. Even though this might not be the best formula for Mathcad, it might be the best in my world.
Werner Exinger, I tried to figure your file out by hand but it is over my head at this point.
You All are extremely helpful and your collaboration is very appreciated.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Gary
"or is that my job or a Moderator's job?" That's yours to do.
I already indicated that choosing more than just the three points will give you trouble with the sines. Gumbel (which somewhat resembles Weibull) distribution might help you better then; as Fred shows.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi All,
I have made a file that compares Luc's equation and mine. I believe my equation is closer to what I need. Luc's is probably very useful though in some situations but it doesn't seem to lend itself to more than three benchmarks. I couldn't figure out how to get a smooth curve when using more than three benchmarks.
You All are a great collaboratory team. Thank you for all of your contributions.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure where you're getting the values for your curve; but you can use the cost function to get a bit better:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred Kohlhepp and All,
I ran your file and the graph that the cst function generated was, overall, better along the benchmarks but it missed at two important points. The peak and the start were not as good as the curve that I tediously iterated. The peak needs to be at 173 or very close and the start needs to have a more asymptotic design. You probably did not know that and I regret that. I had to rename your variables as my F(x) function was using your F2(x) variables.
I tried to research this cst methodology but could not find it in either the Help menu or the internet. I will try to find the cst function and experiment with it.
As the graph now stands, I can use it. I would like to have it be perfect but, ...
Thank you for your attempt(s) and for revealing the cst function.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
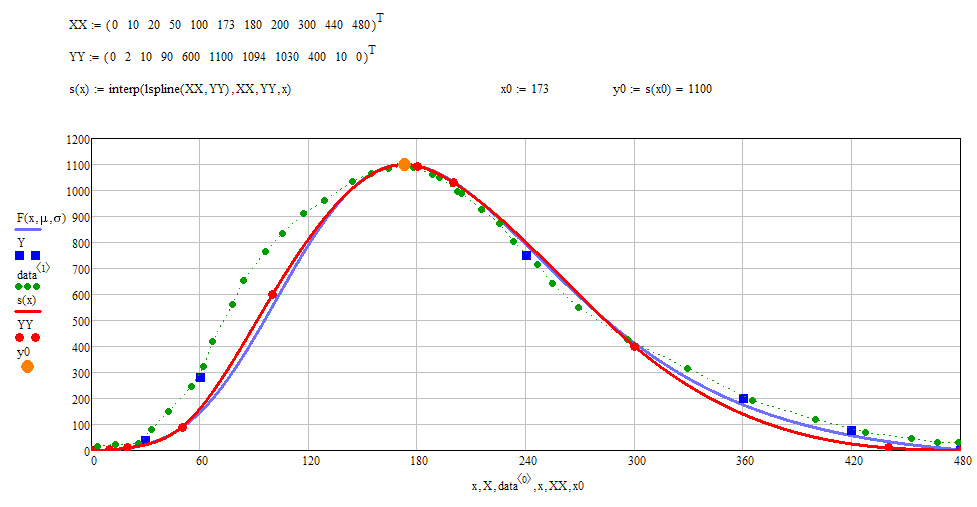
When you first posted your sheet which includes the original picture of the chemical rate (green curve) and this also seemed the reason why Fred took the time to digitize that curve.
But in the meantime it looks to me that you don't care for that original picture at all and you also don't care for the function type used - obviously it does not matter if the used function type really is appropriate for that kind of chemical reaction.
When I look a the last graph you seem to be satisfied with it even seems that you don't care about the additional "benchmarks" you added yourself as you graph (blue line) happily ignores them (blue squares).
Peak at 173/1100 is essential, OK, understood.
Start at 0/0 seems to be important, too, even though the original curves seems not to start at 0/0.
And as I understand it you also want a slope of zero at that point, too. Guess this is what you mean when you talk about asymptotic behavior.
At 480 you would like to see a value as close to zero as possible and probably also a slope as near as 0 as possible. Here you would accept true asymptotic behavior, which would mean that the function is just close to zero and will reach zero just at +- infinity.
As you don't care for a specific type of function and just want to be able to implement the whole thing in PHP - why don't you simply start a simple drawing program. model the shape of the curve using a couple of spline lines which are available in most drawing programs. When you are happy with the shape you created, use the reference points you had set in your drawing and implement spline interpolation in PHP. You find a lot of ready to use solutions for creating splines in PHP if you search.
So you would get the exact curve you are looking for in shorter time.
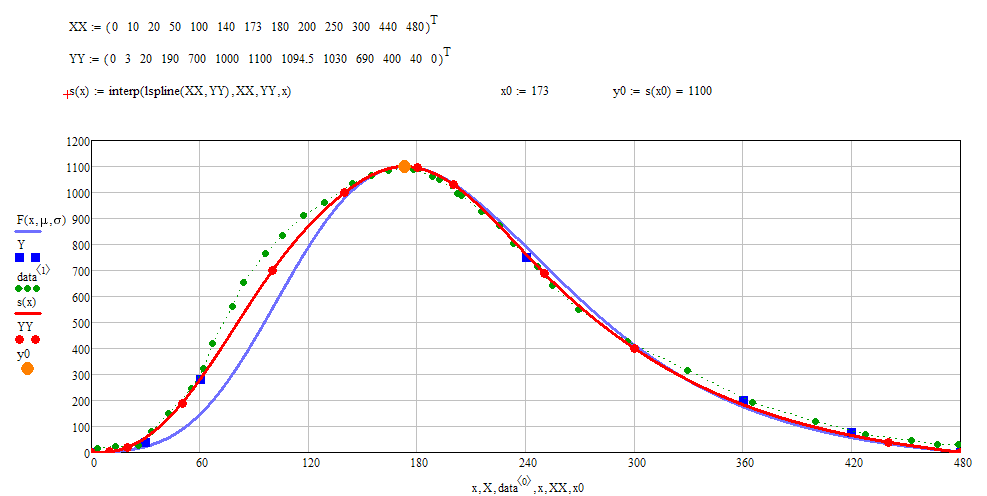
Here are some reference points (red dots, the values you see above) - your 3 benchs and 8 additional ones - for a spline interpolation (red line) which I have chosen (in Mathcad) to be close to your curve (blue).
The green dots are from your original graph using Freds digitized values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is another set of numbers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you look closely you will see that the "cst function," is simply the sum of the errors squared. (The difference between what the value is, (Y) and what the function computes the value to be, squared so it's always positive.) Asking Mathcad to minimize that function by adjusting the coefficients is simply doing a least squares fit to the data. We could have used a "solve block," but minimize works without a solve block so some of the emasculated versions can do this.
More germain to this discussion is the question, "What do you really want from this?" It seems you want to define three points {(0,0), (173,1100), (480,0)} and fit a curve thru them with slopes zero at all three. And, it seems that the shape of the curve between these points is of little concern.
What am I missing?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred Kohlhepp, Werner Exinger, and All,
Fred, you might have come into the discussion at the halfway point(pun intended).
1. I need a curve that focuses on the three main points of Start, Peak, and End.
2. The curve must be somewhat asymptotic at both the Start and the End.
3. The slopes are generally unimportant except that they must be smooth as they will only 'unite or join' the Start, Peak, and End points.
4. The result must be able to be entered into php internet coding as an equation.
5. I will be employing two or more curves or equations at once that will be added or subtracted. Can the cst or Hoerl or interp,lspline functions be addedor subtracted? Can one cst function be addedor subtracted to another cst function to allow generation of a graph? The graph would end up being very flat as one would mostly cancel the other.
6. I am not a math or Mathcad expert so the result should be in an equation form that I don't have to reconstruct or interpret from Mathcad shorthand. I understand little of what you posted. I understand the idea of squaring negatives to get a positive. The rest I don't fully understand or have any experience with. I researched the cst function and found nothing on it so I can't use it. It was not in my Mathcad Help or anywhere that I saw on the internet. It looks like it put out a great curve but I don't know how to use the function and I don't know how to convert it to php coding. I am good at Algebra, Geometry, and Trig. so the equation can be very complex if needed. I don't know if php coding allows for calculus so I am guarded on that method, not that calc would be any good here. I am having trouble finding an answer to that too.
My closest iteration was in the final_chem-rate-both.mcd.zip file above.
Thank you very much for your attention and response. Your work LOOKS great but I don't know how to operate in that environment of 'heavy' Mathcad. If I did know Mathcad like you guys do, I might not need your assistance. Mathcad seems to be loaded with tools to conquer math problems that all of you know well.
At this point, I can use the graph in my final file as it is about 98% good. I wish I did know all of the Mathcad tools but...
You All do fantastic work.
Gary
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Okay. I'm not a php programmer, but this shouldn't be hard to translate:
You have a start, peak and end. We need to calculate two scale factors
between the start and the peak the scale factor is 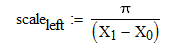 , or 3.14157/(X_peak-X_start)
, or 3.14157/(X_peak-X_start)
between the peak and the end the scale factor is 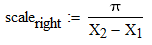 , or 3.14157/(X_end-X_peak)
, or 3.14157/(X_end-X_peak)
Then you write two functions, one for the left side (before peak) and one for the right (after peak.)
The first function is sine the amplitude is half of the peak: 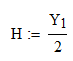 , h = Y_peak/2 and it's sine function, from -pi/2 to pi/2, but scaled to the x value:
, h = Y_peak/2 and it's sine function, from -pi/2 to pi/2, but scaled to the x value: 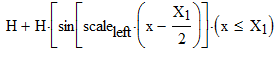 or h+h *sin( 3.14157/(X_peak-X_start)*(x-X_peak/2))
or h+h *sin( 3.14157/(X_peak-X_start)*(x-X_peak/2))
The first function works from X_start to X_peak.
The second function is the cosine from (x-X_peak) to (x-X_end), but the scale factor (3.14157/(X_end-X_peak)) makes that 0 to pi:
 again with : h+h *cos( 3.14157/(X_end-X_peak)*(x)) only for x greater than X_peak.
again with : h+h *cos( 3.14157/(X_end-X_peak)*(x)) only for x greater than X_peak.
Now, I know php has trig functions:



so I think you can code this in php. with a bit of effort.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hallo Fred,
that is essentially the same as what I presented here:Re: graph curve manipulation
Gary wasn't completely happy with it, because it turned out that he had more points to fit.....or so.
Luc





