This is what it looks like (ff=0.075, bb=3) if you follow Valery's suggestion and use that kind of Monte Carlo procedure.
And this is what is should look like (done with PovRay by P. Burke (http://paulbourke.net/geometry/orthocircle/)
What I had in mind was the approach of Viacheslav Mezentsev: http://communities.ptc.com/message/23461#23461
This is the result of Viacheslav's fine method for implicit plots.
Its not raytracig quality but quite good. Drawback is the calculation time. The picture was made with an 80x80x80 grid and took "endless".
If the goal is just implicit plotting you may use other software packages like Maple or Mathcad. But for even better results you may use software like PovRay (see above) or Surfer (http://www.imaginary-exhibition.com/surfer?lang=en).
Forgot to attach the Mathcad sheet in the last post - here it is.
The following pic and the attached animation was done with the free software Surfer (link in post above):
Thanks, Werner - a fine animation!
I see it and think about this 3D surfase - see bellow.
What is its implicit formulа f(x, y, z):=???
Can we create it for next Halloween day? 
PS
Mathcad 15 has 8 outside points for the lighting 3D surfaces
Mathcad MM and Prime Minister has an add one inside points for the lighting 3D surfaces
PPS
Werner, sorry, I see You have a lot of time for Mathcad and PlanetPTC..
Can You help me to translate this text into English?
http://twt.mpei.ac.ru/ochkov/Ellipsoid/index.htm
I hope it will be interesting for Mathcad users.
Valery Ochkov wrote:
Thanks, Werner - a fine animation!
Can be done in minutes using Surfer. The only difficult task being typing in the equation.
The pumpkin would be quite a task modelling by algebraic equations only. But some people are able doing miracles with Surfer. For instance the following by Valentina Galate, suitable for the time soon:
The equations used are:
surface = ((0.99*z-4.7)^2+(0.7*y-2)^2-(0.8*x+3))*((2*z-9)^2+(0.5*y+1)^2-(x+3))*(x+0.8)*((0.5*z-1)^2+(0.8*y+4.3-(0.5*z-0.6))^2-(x+3))+25; surface2 = ((x+1.2)^6+(0.7*y+2.1)^6+(0.8*z+0.5)^6-1)*(0.0001*(x+2)^12+(y+1)^12+(z)^12-0.01); surface3 = (x+2+(0.6*y+1.8))^6+(0.6*y+1.8-(x+2))^6+(0.9*z+0.6)^6-1; surface4 = ((x+2.5)^2+(y-4)^2+(z-2)^2-0.8)*((x+2.5)^2+(y-3.2)^2+(z-2)^2-0.4)*((x+3.2)^2+(y-3.6)^2+(z-2.4)^2-0.2)-0.01; surface5 = ((x+1.7)^2+(7*y-25)^2+(7*z-15)^2-2); surface6 = ((12*(y-2)^2+12*(x+5.7)^2+12*(z-1)^2+2)^2-9*(12*(x+5.7)^2+12*(y-2)^2)-7*(y-2)); surface7 = (0.63^2*x+2.35)^6-2*(0.63^2*x+2.35)^3+1+((z)^2+(y+1)^2-1)^3; surface8 = ((x+2.55)^6+(y+1)^6+(z+0.459)^6-0.0009)*((x+1.445)^6+(y+3.6)^6+(z+1.53)^6-0.005);
I won't try to do it in Mathcad 😉
Werner, sorry, I see You have a lot of time
Thats an illusion 😉
Translations sure are not on my agenda (struggling with English myself - thank you google, leo, dict, etc.). But using google translate in combination with the pics you provide should suffice for us to get the point(s) of your fine article.
Werner Exinger wrote:
The equations used are...
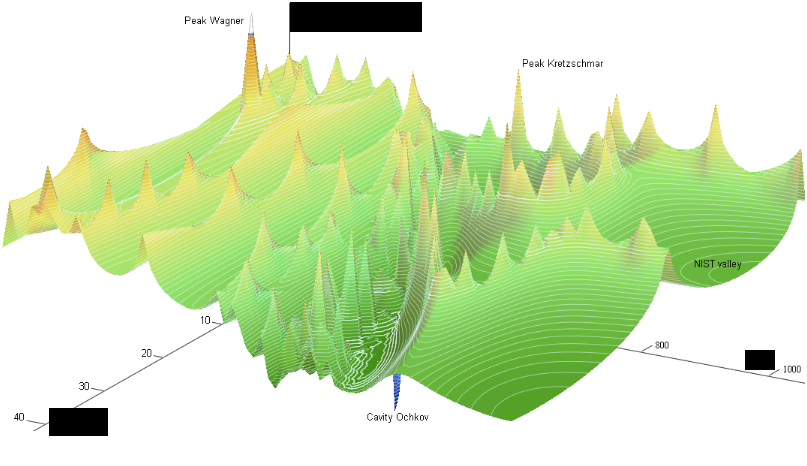
I will show on this seminar this landscape. Do you know what is it - a "material science landscape"?
Werner Exinger wrote:
Looks interesting
Thanks!
As a counter plot too!
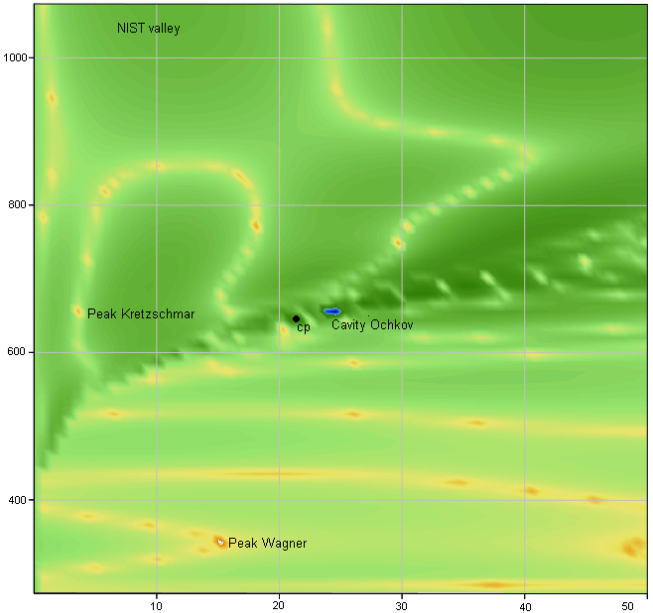But it is not a frctal.
marta janeras wrote:
Valery,
interesting presentation.
About the slide #9, all that companies use Mathcad? How did you get this information?
Thanks!
It was one slide from one PTC presentation.
It is PTC users not only Mathcad.
marta janeras wrote:
I hope that mathcad developers add your implicitplot3d() function in the future versions of mathcad
We have a dreames about old Mathcad 15 tools in Mathcad Prime not about new ones
marta janeras wrote:
I would like my students to create funny or interesting surfaces (like the Halloween pumpkin) with mathcad and print 3D models of the results.
In past we have one MathSoft site for same picture. Where is it now?
