making an Loop with Mathcad

[ycho-3]

what i want to do is making a loop, which can do an iteration work automatically.

In this function, i put the initial value

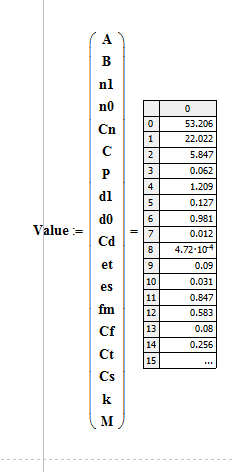
and by using an Minerr optimization, it gives final values(which i defined as Newvalue)

and what i need to do is iteration work

so reusing this Newvalue as an initial value.

for example, if i put n=3, it should mean it iterate 3 times

for that i tried using an While loop.

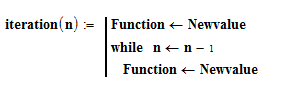
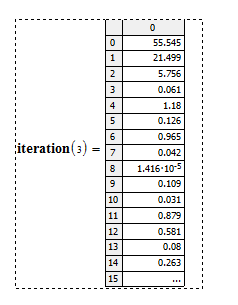
but i think this is not right..because it gives same result eventhough i put different value of n.

can you help me with this problem?

[-MFra-]

Hi Ycho-3, there are inconsistencies. You should correct and then  reattach the file.

Greetings FM.

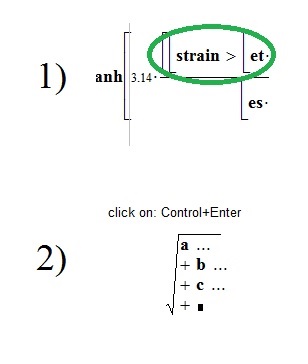
The logical operation, as the argument of tanh, is somewhat unusual. I would avoid as there is enough space to write.

[RichardJ]

Your loop does nothing more than assign Newvalue to the variable Function (which is a variable, not a function, regardless of what you choose to name it) n times. So why do you think the value of Function will change? It is the same as calling the local assignment x<--3 n times. The answer will always be 3.

It is possible to take the results from the minerr optimization and call minerr again with those results as guess values, but it will not achieve anything. Minerr has converged to a minimum, and returns the values of the parameters at the minimum. If you use those values as guess values then minerr will immediately converge to the same minimum, and return the same parameter values.

Perhaps you should explain what your end goal is. What are you trying to achieve?

[ycho-3]

Ultimately what i want to achieve is getting an optimized value even after i put general value(like 1 ) into initial value.

right now it is not possible, if i put general value into an initial value, it occurs an error.

And my professor thought that error will be figured out if i make a loop.

[RichardJ]

Sorry, but it's still not clear. Minerr is iterative. You give is some guess values (your initial values) for the fitting parameters. It then changes the parameters iteratively in such a way that it heads downhill on the error surface. When it gets to a minimum it stops. There is no guarantee that the minimum it finds is the global minimum, and other things, such as flat spots or discontinuities, can also make it stop. If the problem is well behaved then the guess values don't matter much, and it will converge to the same (global) minimum regardless of what they are. If the problem is badly behaved, and as I noted here: Minerr/nonlinear optimizing, yours is very badly behaved, then the guess values matter a lot. There is nothing you can do that will make any downhill optimization method work well with a surface that has discontinuities and multiple minima. You can try different guess values, but in your case there seem to be many minima and/or discontinuities.

In general, taking the results from minerr and feeding them back in as new guess values will get you nowhere, because those values already represent a minimum. In this case it does actually improves the minimization (see other posts in this thread). There is still no guarantee that you have found the global minimum though. Is this what you were trying to do?

[Werner_E]

As I understand you want to use the results of the minerr optimization as guess values for the very same optimization!? Why? Its unlikely you will get different values the second time as Mathcad iterates on its own until it decides that the result is good enough (which admittedly is not always the case).

But you could achieve this by turning the solve block into a function:

[AlvaroDíaz]

Hi Yooney.

I don't think that Einstein could says that "Insanity is doing the same thing over and over again, but expecting different results” because don't apply in a lot of places.

Best regards.

Alvaro.

[RichardJ]

Well, that's a surprise! What you are observing should not happen in a well behaved minimization problem. I suspect the issue is the THE variable, which is discontinuous. Downhill type numeric solvers (which includes all of the minerr algorithms) do not like discontinuities in the error surface. To make things worse, THE is wrapped into d and f, which in turn are wrapped into the return value of Fit(X, Delta). So I suspect there are actually many discontinuities in the error surface, and they cause minerr to stop at arbitrary points. Restarting it at those points allows it to go downhill again until it hits another discontinuity, and again stops.

[AlvaroDíaz]

Hi Richard. Very good point. Actually, round off errors can be interpreted in the same way.

Best regards.

Alvaro.

[ycho-3]

wow i think you are genious!! thank you.. my life saver

[RichardJ]

If you pass the vector of residuals, rather than the sum of the squares of the residuals, to minerr it finds a better solution in fewer iterations, and does so about 70x faster. Note that some of the parameters are very different to the ones found in your best solution

It also shows a points I have tried to make in other posts. The fact that this version finds a solution with smaller residuals means that the solution you found was not the global minimum. I would also be surprised if the new solution were the global minimum. Which brings us back again to the question of what Yooney is trying to do, because if it is to find the global minimum, this approach will not work.

[AlvaroDíaz]

Hi Richard.

Considered f(x,y) = cos(x*y) So, max(f) = 1. But this global maximum happen into a set of the parameters x,y, for example, at any y if x = 0. This is an entire line.

For a general problem, you must to ensure first to have all the local max or min before globalize them, to the highest or lower value. But it global extrama could happen in a very extense set of parameters values.

So, question is about to what can be called a solution under the concepts of numerical calculus. For infinitesimal calculus, you play with the infinity's, and can think in exact solutions. When apply an algorithm, it must to stop at sometime, under some stop criteria. From http://people.duke.edu/~hpgavin/ce281/lm.pdf this is:

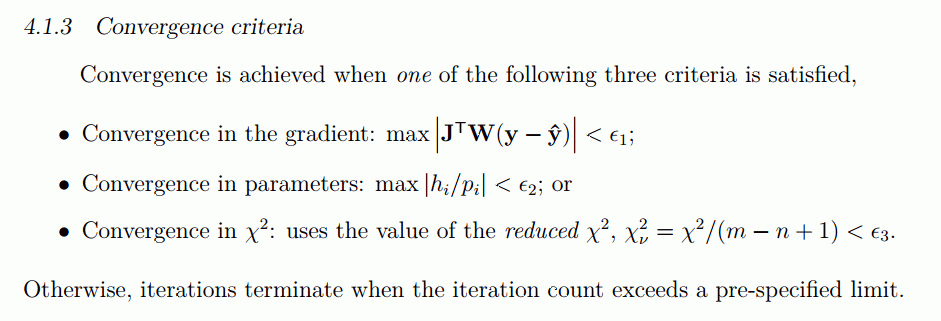
The global min exists as real number, and like other reals, you can found approximations for it, which in this case is based on some set of the parameters. With some good look, this punctual set of parameters could be an approximation for some punctual set in the (assumed) very complicated set of actual solution.

Best regards.

Alvaro.

[ycho-3]

Hi AlvaroDiaz

Actually i have a one more question related with the file you attached.

If i want to fix the value of A,B,n1,n0,Cn, then how can i advise the original file?(still using the iteration loop) can you give me any advise?

for example, fix the 5  initial value  A=1,B=2,n1=3,n0=4,Cn=5 so after the optimization, these values should not change.(same value as Initial values)

and rest of the values(C,P,d1,.....M) would be changed after optimization.

Best regards

Yooney

[RichardJ]

Just take them out of the minimization. However, doing so results in a non-physical solution with huge errors.

[AlvaroDíaz]

Hi.

Richard gives the answer: don't include the values that you want to set as fixed as parameters for the function. With that they are excluded from the minimization block.

But Richard set they as 1,2,3,4,5, and I guess that those values are just as examples, but not actual values. In the Richard's file just delete the yellow assignments for those parameters.

Remember that technically parameters are nothing. What are well defined are variables and constants. There are well defined criteria's, like the derivative, to determine if something is variable or constant.

Parameters are a practical concept to point to something that can vary, but not too much, and eventually, can remain as constant, like caloric capacity Cp, or electrical resistance R, that sometimes are constant, and others function of the temperature. The usual criteria to do that is that if the variation of the dependent variable is small for some range of the parameter, then it can be take as constant for some kind of study.

Best regards.

Alvaro.

[RichardJ]

But Richard set they as 1,2,3,4,5, and I guess that those values are just as examples, but not actual values. In the Richard's file just delete the yellow assignments for those parameters.

Yes, If the question is not read so literally the problem of a non-physical solution goes away. That is the danger of posting a question to a forum populated by mathematicians, scientists, and engineers .

A favorite joke of mine:

The programmers wife is busy preparing dinner, and realizes she forgot to buy a couple of things earlier in the day. She says to the programmer "could you please go to the supermarket and get a loaf of bread. If they have eggs, get a dozen". The programmer returns with twelve loaves of bread.

[AlvaroDíaz]