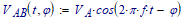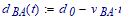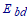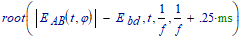- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
maximization problem (voltage stress)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
maximization problem (voltage stress)
In the attached Prime 8 file I'm trying to solve a problem I have invented in my head. I have 2 metal plates, one is fixed and the other is moving toward the other very rapidly (e.g. 1000 mph). The voltage between them varies sinusoidally at 60 Hz. The air between the plates is assumed to breakdown at 3 kV/mm.
I want to vary the phase angle of the applied voltage and find the phase angle that results in the maximum voltage stress across the air in the gap. But, I'm not sure how to find that maximum in MCAD.

Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You ask for the 'stress' in V/m...? That is a maximum of 3 kV/mm, and phase shouldn't play. I guess you want the maximum voltage between the plates.
With, the voltage between the plates as a function of time and phase:
The distance between the plates as a function of time:
The electrical field strength between the plates becomes:
This field strength doesn't exceed the breakdown field strength
within one cycle of frequency f, because the plates aren't close enough.
But just after the first cycle there is an opportunity. The time point that happens is found with:
(where 0.25 ms is a lucky guess)
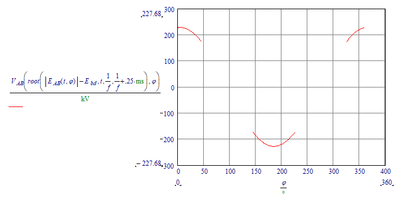
We can fill that into the function for the Voltage between the plates and plot it against the phase:
(Hmm, maybe phase does play a role even for electrical field strength, considering that for two ranges of phase no root is found.)
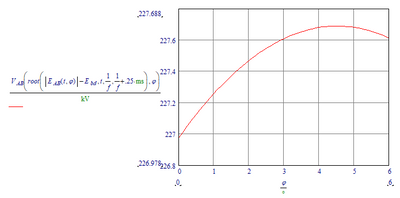
zooming in we find that the maximum voltage occurs at a phase of about 4.5 degrees:
The other point (for a negative voltage) must lie at 184.5 degrees.
A bit more precise, taking the derivative of the curve with respect to phase and finding where it becomes 0, the maximum gap voltage occurs for a phase:
(and thus also for 184.515°..)
I hope this helps.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You ask for the 'stress' in V/m...? That is a maximum of 3 kV/mm, and phase shouldn't play. I guess you want the maximum voltage between the plates.
With, the voltage between the plates as a function of time and phase:
The distance between the plates as a function of time:
The electrical field strength between the plates becomes:
This field strength doesn't exceed the breakdown field strength
within one cycle of frequency f, because the plates aren't close enough.
But just after the first cycle there is an opportunity. The time point that happens is found with:
(where 0.25 ms is a lucky guess)
We can fill that into the function for the Voltage between the plates and plot it against the phase:
(Hmm, maybe phase does play a role even for electrical field strength, considering that for two ranges of phase no root is found.)
zooming in we find that the maximum voltage occurs at a phase of about 4.5 degrees:
The other point (for a negative voltage) must lie at 184.5 degrees.
A bit more precise, taking the derivative of the curve with respect to phase and finding where it becomes 0, the maximum gap voltage occurs for a phase:
(and thus also for 184.515°..)
I hope this helps.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Luc. I will go through what you have done. Phase is the key because the velocity (as you see in the file I attached to original post) is 1000 mph. The plate covers 25 feet in close to 1 cycle.