Sigh!!
Why don't you ask what you really want to know?
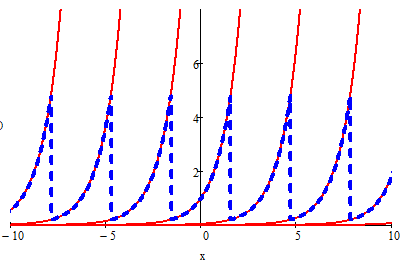
You sure have plotted that sick function and wondered why it looks the way Mathcad is showing.
The answer is (again!) AMBIGUITY - I guess I've mentioned that once or twice. And this time its not the complex domain but simply the atan-function (you may add pi to the result as many times you like).
The min obviously is 0, the real max is infinity of course, Mathcad's max is exp(pi/2).
Look at the plot below:
Red is your function (rather: relation) from a mathematical point of view - an infinte number of exponential functions,
Blue is what Mathcad turns your "function" into as it tries to make a unique function.
atan(x) will only return values from -pi/2 to pi/2. Thats the reason the blue curve has a max at exp(pi/2).
So in Mathcad atan(tan(9*pi/4))=pi/4, while mathematically its pi/4 + k*pi, k=integer
I greatly appreciate your explanation, Werner 
. And I think I don't understand about only three of the followings: ( and I'll try learning more about those. )
Regards.
And I think I don't understand about only three of the followings
OK. I'll try my best.
.PNG){kind=small}
Many functions and operations in mathematics do not yield a unique result but more than one, maybe even an infinte number. You encounter this effect very often especially when you deal with complex numbers (exponentialisation of a complex number or taking the logarithm of a complex number). But also if we stay with real numbers only, we have functions like the arcus function which yield not just a single unique result. Pocket calculators usually decide to select just one of those results, often called the principal value. Mathcad does so, too, most of the times.
.PNG){kind=small}
This is exactly what I was just talking about. Draw a unite circle and look where 9*pi/4 is located, or 17*pi/4, etc. They all are at the very same postion (pi/4, 45°). So the tan() of all those values is the same (1). When you now take the atan(1), all those values are valid results, so atan(1)=pi/4 + k*2*pi. But what about 5*pi/4 (or 13pi/4, or -3pi/4,...) They also are located at the same position (225°) and their tan() is also 1 (tan(x) has a period of pi). So atan(1) is also -3pi/4, 5pi/4, 13pi/4, ...etc. So combining all the above gives us that atan(1)=pi/4 + any integer multiple of pi. And atan(tan(9*pi/4))=atan(1)=pi/4+k*pi, k=integer.
.PNG)
Great! Matcad's symbolics is aware of two kinds of ambiguities here (most often it is not) and so using "fully" yields even a mathematically correct general result. But the check must fail because of Mathcad's attempt to yield unique results (which is a good thing given what Mathcad is made for).Let alone the complex result you selected. Lets chose more simple x=pi, which is a solution of your equation, too. (_n=1, _k=0).
When you check, Mathcad first calculates tan(pi). The result is of course 0 (thats unique). Then Mathcad has to calculate atan(0). Mathematically atan(0)=any multiple of pi= .....-3pi, -2pi, -pi, 0, pi, 2pi, 3pi, .....
Any of those values is a valid result - what should Mathcad do? Not surprisingly it selects 0. atan(x) defaults to the range (-pi/2; pi] as its also the case with most/all calculators. So your expression gets e^0-e^pi=1-e^pi and not 0. Thats life! In other words D(pi) has an infinite number of results, one of them is 0, one is 1+e^pi and there a lot of otheres, too.
One word about how functions are implemented in Mathcad and a try to guess why Mathcad sometimes seems to be aware of ambiguities and sometimes its not.
Mathcad is aware of the fact, that the equation tan(x)=0 has an infinite number of solutions
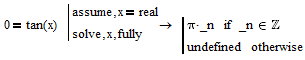
but the atan() function is implemented as a unique function and so Mathcad does not see any ambiguities here
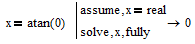
This is very similar to squaring and square root. While the equation x^2=4 has the two solutions +2 and -2, the sqrt(4)=2 (and not -2). There is a commonly ageed on mathematical definition that the square root is just the positive value (with the exception of 0).
( and I'll try learning more about those. )
Great, but don't use Mathcad to do so!
I have written it already in a previous post some time ago: If you want to learn more about math, stick to the books.
Mathcad IS NOT mathematics!!
Mathcad is a great tool to use if you already have a decent math knowledge about what you are doing and you often need that knowledge to be able to interprete Mathcad's results. But Mathcad sure is a lousy teacher. If Mathcad gives you no solution it does not mean that there is no solution. If Mathcad gives you a result which seems to be wrong, it may just be a matter of interpretation (as with the seemingly wrong check above) or in some rare cases it may be really wrong, too.
So you can't blindly trust the results of any math program. The math has already to be in your brain, the program is just the tool.
So gather some math textbooks about subjects which are of interest to you and carefully study those rather than to try to get Mathcad to teach you - it won't do so.
I greatly appreciate your time and help, Werner. . I got it. , but only one thing :
and I got stuck it here. In other words, what is a input, value of x, would make the output, D(x) := e^atan[tan(x)] - e^pi, equal to 0.
Best Regards.
and I got stuck it here. In other words, what is a input, value of x, would make the output, D(x) := e^atan[tan(x)] - e^pi, equal to 0.
The answer depends.
Mathematics:
e^atan[tan(x)] - e^pi has an infinite number of results for any value of x. Its not unique because of the atan() function and if we accept complex numbers, too, because of the e^() as well. So strictly spoken the expression never simpifies to 0 alone but is always an infinite number of values. If x is any integer multiple of pi, one of those numbers is zero. Even more possibilities if you accept complex values, too - Mathcad had shown you how.
Mathcad:
Only x=0.
But remember:
