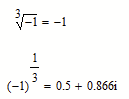Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
numerical solution of a differential equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
numerical solution of a differential equation
Hello,
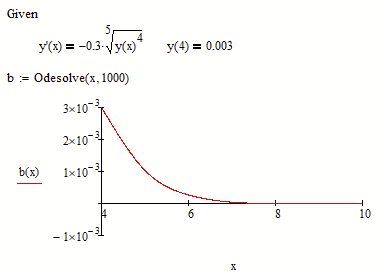
I would like to solve the differential equation in the document. However, Mathcad can only calculate the values if I use a positive factor. In Python the values are calculated without any problems. What am I doing wrong? The problem exists in Mathcad 15, as well as in Prime 6.0.
Thank you very much for any hints.
Best regards
Paul
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
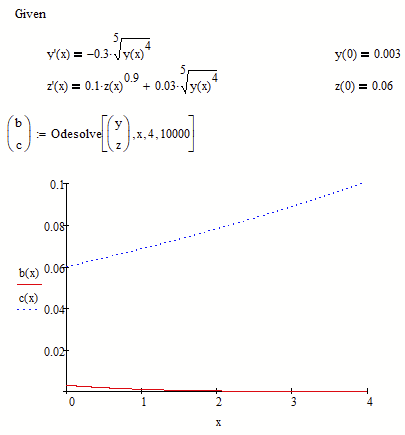
Mathcad chokes on the different x-values in the initial conditions (0 for z but 4 for y).
Are you aware that the second argument of the odesolve function is the endvalue for x?
The start value is taken from the initial conditions and so Mathcad runs into troubles if it encounters two different "start" values.
Here is what you get with 0 as the start value for both (and 4 as the endvalue). The last arguement of odesolve is the number of calc steps and is optional.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad doesn't like the imaginary components you get from y(x)^0.8 when y goes negative. Taking the real part works ok:
What does the Python result look like?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's another workaround
The root function is implemented in Mathcad so that it returns the real value, not the main root (the one with the smallest positive phase). Actually in math a power with a rational exponent is defined only for non-negative bases.
See for example
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hey Alan and Werner,
thank you! You made my day. I thought Mathcad can't do it and I have to calculate everything externally.
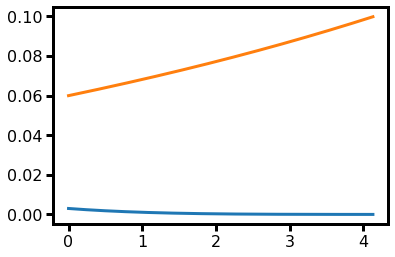
Here you can see the result from Python. So it matches. 🙂 blue line=y, orange line=z
Now I have another challenge. If I solve the previous equation together in a differential equation system, Mathcad says "Convergence to one solution not possible, too many integrator steps" No matter which method or which step size I choose, the problem remains. Do you have another hint for me?
Thank you very much.
Best regards
Paul
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad chokes on the different x-values in the initial conditions (0 for z but 4 for y).
Are you aware that the second argument of the odesolve function is the endvalue for x?
The start value is taken from the initial conditions and so Mathcad runs into troubles if it encounters two different "start" values.
Here is what you get with 0 as the start value for both (and 4 as the endvalue). The last arguement of odesolve is the number of calc steps and is optional.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you once again! I was indeed not very familiar with the odesolve function. In Python, both initial conditions start at 0. That's why there were no problems there.
I have now helped myself like this. I first calculate the first differential equation with y(4)=0.003 and then determine b(0)=0.052. I then use this value in the differential equation system as the new initial condition y(0)=b(0)=0.052.
It should work like this. Perhaps there is a more elegant way.
Thanks again for your help.
Best regards
Paul
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As your first ODE does not depend on z your approach of solving them one after another instead of a system looks straight forward to me.
I lack experience with ODE systems with different initial values.
It may be that the functions "bvalfit" and/or "sbval" can be of help, but I never had used them. You'll have to look them up in the help.
Here from the help of MC15:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hey Werner,
thanks! I will have a look at this function. If I find a better solution for this kind of problem, I will post it.
Cheers.
Paul