Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
odesolve
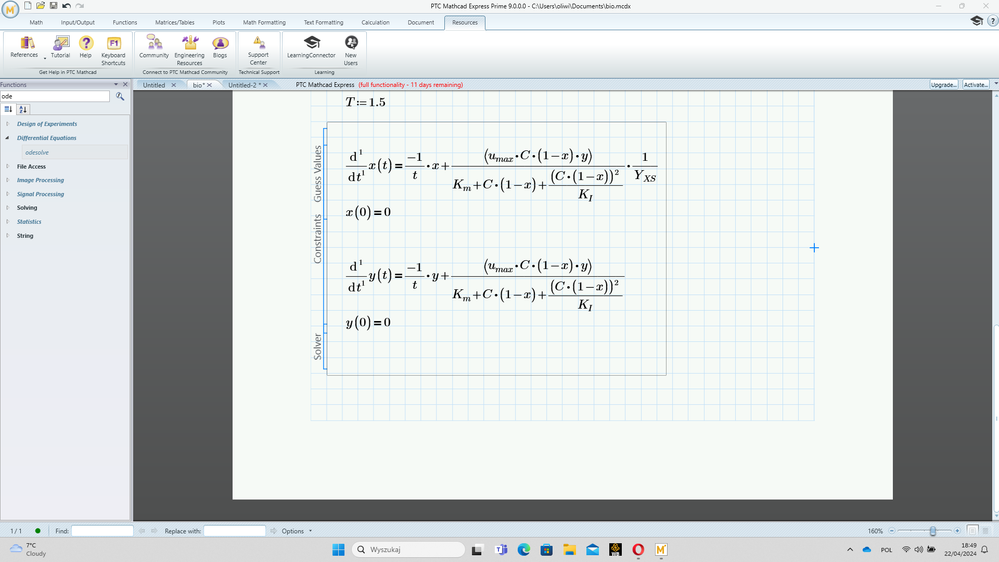
Hey, I have problem with system of differential non linear equation. I dont have any idea how to solve this. I hope you will help me 🙂
- Labels:
-
Chemical_Engineering
- Tags:
- odesolve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I assume that everywhere on the right-hand-side of =, where you use x, you mean x(t) and where you use y you mean y(t).
If that is so, you should write them as such.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc already noted the missing arguments when you wrote x and/or y.
For further help and if you have troubles with the usage of "odesolve" it would be necessary that you attach your worksheet.
Prime's help is not much helpful and I guess there is not a single example showing how to use odesolve to solve a system of ODEs.
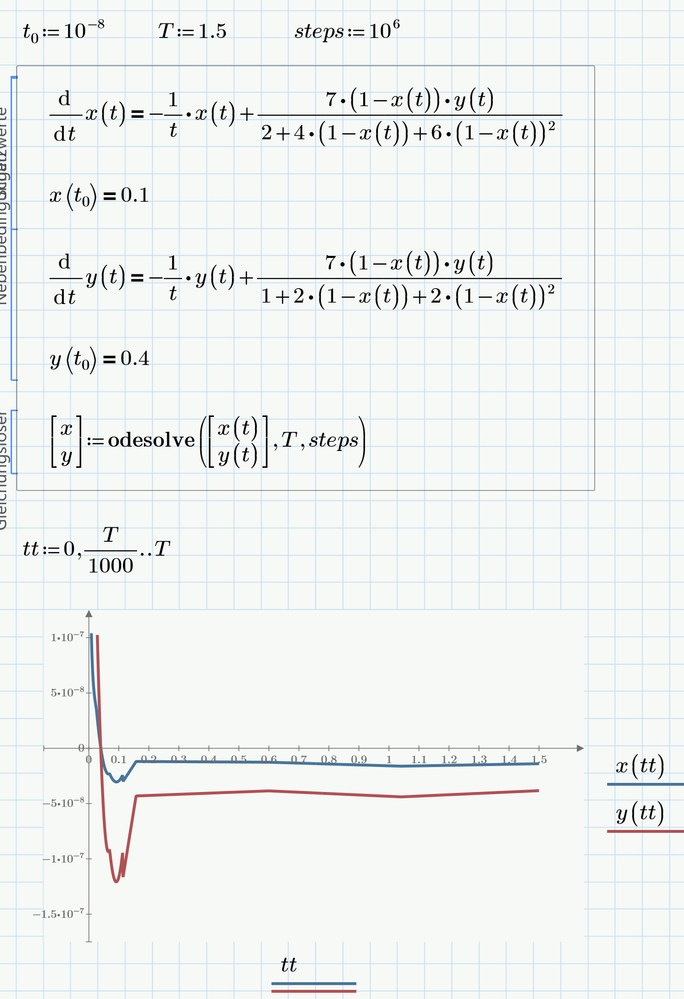
In your case you may run into trouble when using t=0 as starting value because of the expression 1/t in your equations (division by zero).
Here is an example. I changed the starting value to t=10^-8 and also the initial conditions to 0.1 and 0.4.
If I demand the initial values to be both zero, I would end up with constant functions x(t)=y(t)=0 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The system of equations is given in explicit standard form. The right sides are continuous. According to the theorems about existence and uniqueness, exactly one solution exists with initial values. It is easy to see that the zero solution is the only solution to solve the system.
Another way to this solution:
Multiply the first equation by Yxs and subtract the second equation. The large term on the right side is omitted. The difference function z(t) must then satisfy an equation of the type z´(t)=-z(t) with z(0)=0. Here too, only the null solution is possible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Addition and correction:
The problem cannot be solved in the form presented because the initial values are not in the continuity region of the right-hand sides. It is only possible to give a general solution, including the zero solution, without these initial values. Or to represent the problem (as Werner did) initial values close to zero but in the continuity range are chosen.
It is interesting to examine the difference function mentioned. The equation type is: (correction) z´= -(1/t)*z with z(t)=x(t)*Yxs-y(t) and general solution (separation of the variables) z(t) = K/ t with K>0. In this respect, it can be expected asymptotically that x(t) and y(t) differ less and less.