Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
plotting a circle using points of triangle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
plotting a circle using points of triangle
Hello, i am studying master program at mechanical engineering. I am trying plot a circle using 3 points of a triangle. Circle must be plot inside triangle. How can i do? I have done my first homework but second is harder for me. I am using mathcad 15.
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
henry leung wrote:
Can anyone help me to make this file work?
Not anyone - only Werner!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats exactly the problem with vectors and solve block. Mathcad can not know the dimensions of E and so you would have to provide the elements and again we don't have a pure vetcorial solution.
The best we can achieve is a solution using complex number (similar to Alan's) instead of vectors.
A workaround is attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Vectors, complex numbers...
KISS- 3 simple (transparent!) equations with 3 unknown r, x.r and y.r. Numerical or symbolic solution and no problem!
See one more animation in attach.
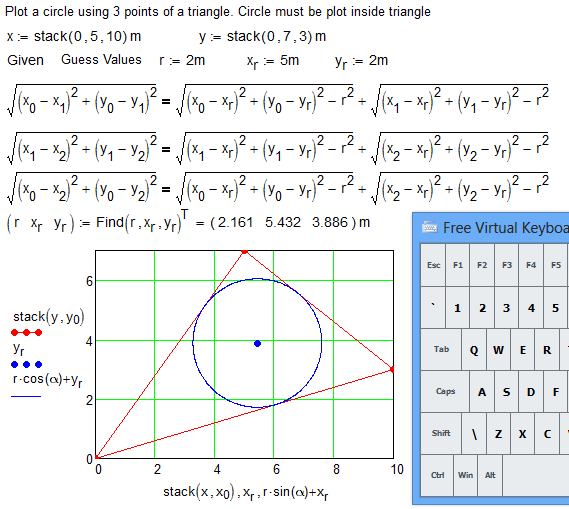
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
The best we can achieve is a solution using complex number (similar to Alan's) instead of vectors.
Whatever you can do with complex numbers you can do with vectors, of course - see attached. But this still doesn't help with the symbolic solution.
I'm inclined towards Valery's view that his approach is the simplest, especially for novices. That said, there is a pleasing elegance about a vector approach!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Simplest solution - a cloud function! ![]()
Do You know more simple solution this task?
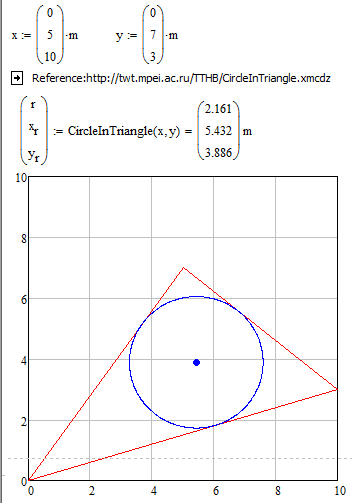
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's yet another approach (still numerical) that finds the coordinates of the points where the circle touches the triangle at the same time as finding the coordinates of the circle centre and the circle radius.
I think enough is enough though. An interesting problem but time to move on!!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok. Just for you Valery. Here's a 3D version of my previous post. But I'm definitely not going to do anything about a 4D version!
Alan
Message was edited by: ALAN STEVENS Worksheet replaced with a more sensible one!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan!
But...
Einstein said and Werner pointed for us one more that: "Make everything as simple as possible, but not simpler!"
You solution is "simpler" ![]()
We have 4 unknowns r, rx, ry and rz and I would like to see the solution of 4 equations, "but not simpler" - 16 equations.
OK!
One subsidiary problem.
We have three segments (or 4), which are known that its are bisectors of one triangle (tetrahedron). Is it possible with a compass (циркуль) and straightedge (линейка), pardon it is unpossible, with Mathad to construct this triangle (tetrahedron)?
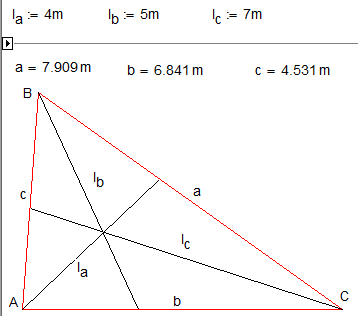
.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
One subsidiary problem.
We have three segments (or 4), which are known that its are bisectors of one triangle ...
Do you mean that the angles are bisected or that the sides are bisected?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Valery Ochkov wrote:
One subsidiary problem.
We have three segments (or 4), which are known that its are bisectors of one triangle ...
Do you mean that the angles are bisected or that the sides are bisected?
Alan
Angle - a angle bisector, not median.
Sorry for my English.
The angle bisectors crossing is in our triangle a center of our circle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Angle - a angle bisector, not median.
Too late! I did both just in case. ![]()
I used Heron's formula in both cases - see attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Valery Ochkov wrote:
Angle - a angle bisector, not median.
Too late! I did both just in case.
Alan
Sorry, not to late - KISS ![]()
![]()
![]()

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Very neat - I like it!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
Very neat - I like it!
Thanks, Alan!
I have a lot of "neat" ideas for the book "Geometry with Mathcad" but no time to do it. And second - it will be good to write this book in English too but Ai knou Inglish not khorosho...
Let us develop this Group - http://communities.ptc.com/groups/fine-math-curves-in-mathvad
- « Previous
-
- 1
- 2
- Next »






