Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
plotting an abitrary polyhedron
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
plotting an abitrary polyhedron
I have MathCad 14.0 and would like to plot a 3-D polyhedral surface from a set of (x,y,z) vertices. I could not find any plotting option/function to this - am I missing something? Does MathCad 15 have this functionality?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is nothing built-in, but if you download and install this e-book you will have more functions for plotting polyhedra than you know what to do with ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
chris jekeli wrote:
I have MathCad 14.0 and would like to plot a 3-D polyhedral surface from a set of (x,y,z) vertices. I could not find any plotting option/function to this - am I missing something? Does MathCad 15 have this functionality?
I can't have that functionality because a set of vertices does not describe a surface! You would have to provide the information which vertices form an edge and which a tile. Being no 3D CAD software Mathcad's posibilities are limited and a surface is built by quadrilateralso only. But the "Amazing Images" E-Book Richard pointed you to does more most of us where aware that could be done.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
a set of vertices does not describe a surface!
In general that is of course true, but are you sure it's true when the surface is specified to be a polyhedron? If the surface is a polyhedron then I think the vertices must be on a 3D convex hull, and that is enough to determine the edges. I may well be wrong about that though, because I certainly do not have any proof ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
a set of vertices does not describe a surface!
In general that is of course true, but are you sure it's true when the surface is specified to be a polyhedron? If the surface is a polyhedron then I think the vertices must be on a 3D convex hull, and that is enough to determine the edges. I may well be wrong about that though, because I certainly do not have any proof
I am not sure, either, but I guess you are assuming that the polyhedron is simply connected and convex, which was not stated by the OP.![]() This does not mean, though, that I would know of a simple way to create the necessary data structure in MC for a convex polyhedron.
This does not mean, though, that I would know of a simple way to create the necessary data structure in MC for a convex polyhedron.![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all for your responses. Given the vertices one would need to do some kind of three-dimensional triangulation and then plot the faces of the polyhedron, which should be possible even if it is not concave. Alternatively, one could create a regular data grid and interpolate function values from the vertices and plot a surface. These are a couple of options in Matlab that may be a future functionality also in MathCad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
chris jekeli wrote:
Thank you all for your responses. Given the vertices one would need to do some kind of three-dimensional triangulation and then plot the faces of the polyhedron, which should be possible even if it is not concave. Alternatively, one could create a regular data grid and interpolate function values from the vertices and plot a surface. These are a couple of options in Matlab that may be a future functionality also in MathCad.
Yes, some kind of triangulation would solve the task, but you would have to provide it yourself along with the points to make for a unique solution. If only a bunch of arbitrary points in 3D space are given, there are numerous ways you can create a polyhedron with those points as vertices. No software can read your mind to determine which of the many solutions is the one you would prefer. Of course a software could chose one of the many solutions at random and create the necessary data structure to plot it and I guess it would be possible to write a Mathcad routine to do so.
Maybe the problem can be better understood in 2D. The task would be to plot a polygon when only the vertices are given. The solution is not unique again as you can see in the pics below - just 3 out of 24 ways to create a polygon with the 5 given vertices.
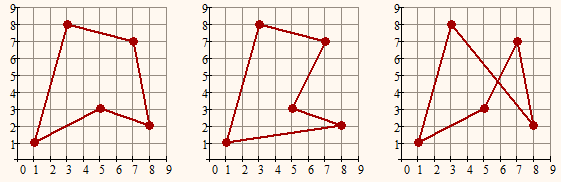
So a bunch of points in 2D don't define a polygon, a bunch of points in 3D don't define a polyhedron.
The situation is different if its possible to form a convex polygon/polyhedron with those points (which is very unlikely for a bunch of randomly chosen arbitrary points). Then this convex polgon/polyhedron would be the convex hull of the points and is unique.





