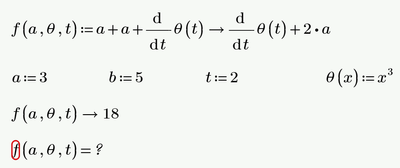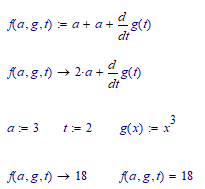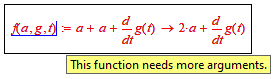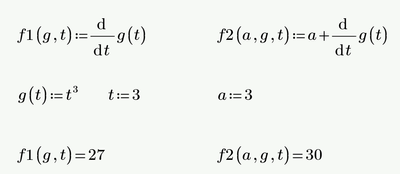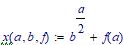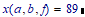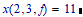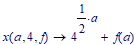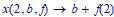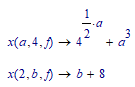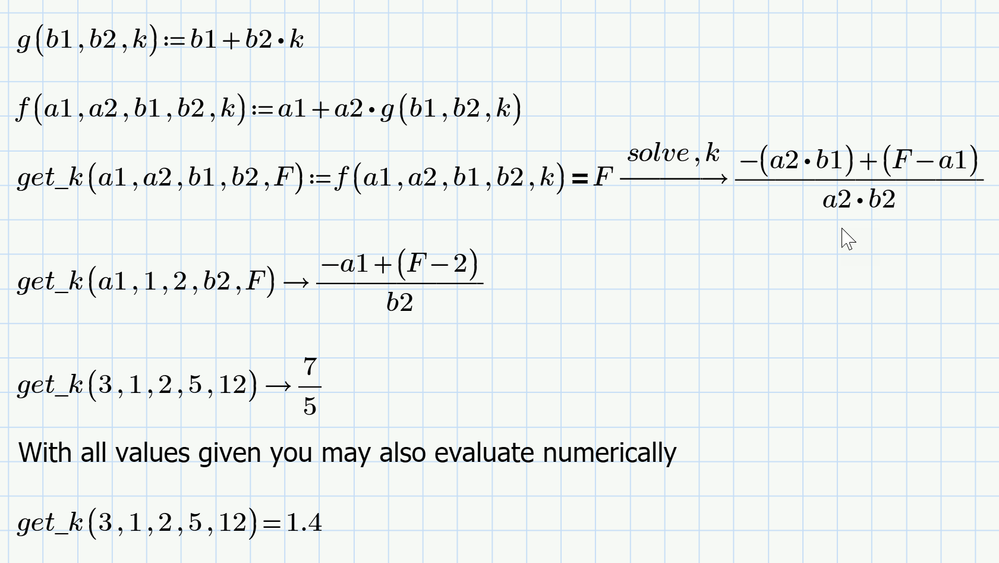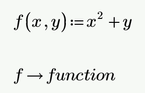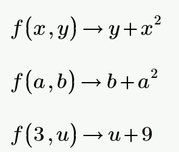Thank you for your answer.
I now try another approach:
1-define completely the symbolic formula
2- then i will define numerical values of known parameters
I expect so to see the formula with some numerical values.
In the following formula, the result seems unknown, as I would have expect on 2nd line to have the same than 1st line.
You must realize the difference between numeric evaluation (=) and symbolic evaluation (->)
Here some remarks using a simpler example
BTW, even in the last approach a derivative won't work (IMHO it should, but maybe its because Prime would have to do the numeric derivation at definition time which it can't because the function is unknown at that time?)
nor that way
It look like its a new Prime 10 bug!
It still works OK in Prime 9
Prime 9:
Prime 10:
Error message means "A function or variable name is needed".
I can see no meaningful reason why f2 should fail but f1 would work OK.
Again - any expressions. either typed in or derived by a symbolic operation like "solve" is static in the sense, that variables defined later will not be replaced in that expression if you evaluate it.
Only way out is to define it as a function.
As already shown you may define variables and functions but make them inaccessible for the symbolic engine.
That way you can make an expression evaluate numerically using the numeric evaluation (=) and still have the symbolic result at hand if you evaluate it symbolically.
"At the end, I need to see better which are preponderant terms of the formula and understand better how it behaves."
Exactly for this purpose it is MUCH better if you define a function with parameters. Elaborating on Werner's example with:
you can have the numerical result:
or another one:
AND you can see how a specific variable is handled, such as a:
or b:
And if you do NOT clear the symbolic for f:
Success!
Luc
Thank you for your proposal.
I am currently trying it but facing a simple issue to build the final formula:
In your example the value of k would not only depend on a1, a2, b1 and b2, but also on the value given by function f. I call this value F in the screenshot below.
You could do as follows:
again thank you very much for your answer
I try to follow your example, but very quickly it says there is no solution, although I am sure there is one
Don't ask me why, but Prime fails because of the function Load.axial in the parameter list.
Maybe because the solutions does not directly depend on that function, but the logic behind that failure is not really clear to me at the moment.
But anyway, once you delete Load.axial from the parameter list of your function get_LoadPinch..., Prime is happy and returns a result:
EDIT: OK, I guess a have a logical explanation for Primes failing when you apply the function name as a parameter. Doing so would you enable to provide different functions Load.axial. But Prime tries right ahead to find a solution even though now the function Load.axial is unknown. But this function has the variable you want to solve for as an argument and because Prime does not know what the function looks like its quite clear that it can't give a symbolic solution.
We would need some kind of late evaluation which triggers the symbolics only when the function is called with a specific function Load.axial as its argument, but this is not an option in Prime.
Here a simplified example
Interesting point, thanks a lot.
Now I come almost to the end.
I have my symbolic formula.
I define some numerical values
I would like to get 'simplfied' formula where all calculation that be done and simplified appear done
and ideally with a factor or the symbol "I"
What should be used as keywords to get a kind of clean and understandable equation ?
I had a quick look but actually I am lost as of the large expressions because of your huge long variable names.
Maybe I'll have a second look tomorrow if times allows.
EDIT:
I had a quick second look and moved the unit (re)definitions to the front of the sheet, where they belong (in front of any variable definition) and also labeled then as units (see the bold blue type face).
I also added gm := 10^-3 kg
See attached file
If you need more unit simplification you have to tell the symbolics so likewise.
The last expression yields something like sin(function) and I tried to find out where this may stem from but I got completely lost in your (for me) much too large expressions with all those lengthy variable and function names. All I could see is that this strange expression also occurs in the definition of your function get_LoadPinch but I was not able to trace any further.
I guess I can't be of help anymore here...
EDIT2: OK, I couldn't resist 😉
Found the root of the problem:
Here some thoughts which may help tiding up the worksheet, making the expression a bit shorter and maybe better readable:
You may of course combine the methods, create a function with two or three vector arguments, etc. - whatever seems appropriate.
After fixing the aforementioned problem with gamma we get a symbolic result, but there are one or two unit problems you'll have to fix!
Prime 9 sheet attached
@FB_10651590 wrote:
Great! thank you so much!
I am new to Prime but finding the error seems a litttle complex,
the case of the 3 arguments of Gamma was not easy to find as not clue from Prime.
Anyway thank you for your patience.
Now I need to find this unit problem.
It wasn't easy for me, too because of the large expressions and variable names.
Prime's symbolics can't give any clue because it doesn't see it as an error.
If you define a function and evaluate just the function name, all information you will get is that its a function.
This is exactly what happened when you used just the function name gamma.
Only when you provide function arguments the symbolic will evaluate the function using the definition
One idea to make the expressions in your sheet a bit smaller would be to make all functions only dependent on the few arguments you need.
It looks like you just want the result be dependent on the four arguments I, Acc.Mot, Fr.Axial and K0.
So you could define the other variables at the top and then define all functions only dependent on those four variables.
According the unit mismatch I can't help. Its either in the formulas you used or in the variable definition (or both). Good luck!
