Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
smoothing with movavg creates offset ??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
smoothing with movavg creates offset ??
hi all,
i'm using prime 2. when i smooth some data with the movavg function, the resulting data is offset by the size of the smoothing window. in fact, even the helpcenter example on using moving average to smooth data shows this resulting offset! but with no comment. attached.
is this a bug or am i using movavg wrong?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a suggestion for a symmetrical moving average window
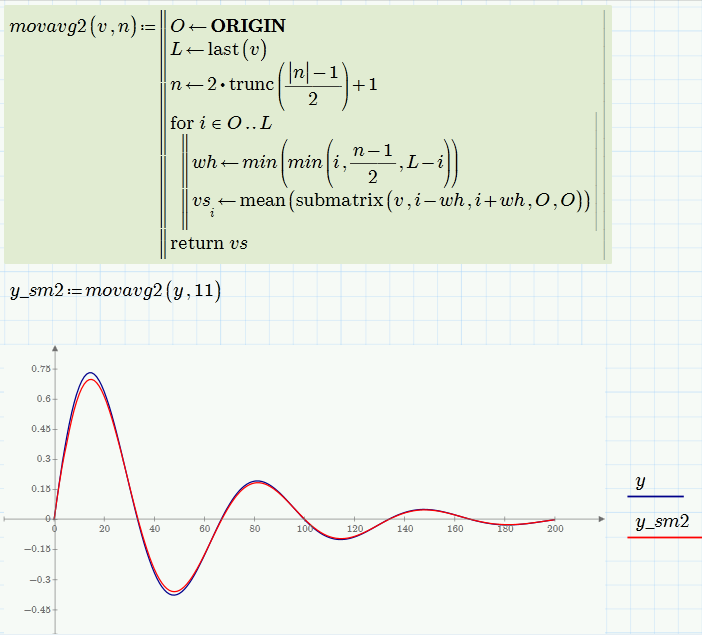
The attached file is in P3 format, so your P2 will not be able to read it - therefor the pic.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> is this a bug or am i using movavg wrong?
Neither of the two.
Its simply the way this algorithm works and its explained in more detail in the Data-Smooth-Example. Here the help clearly states
Note Large window widths introduce a time lag. |
The reason is that only values to left of the time value are used for calculating the average. You might consider writing your own routine using a synmmetrical window.
Or maybe "medsmooth" or "medfilt1d" (deprecated but still available; replaced by "medsmooth") are more suitable for your purposes.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Note
Large window widths introduce a time lag.
Yes, a decidedly inaccurate statement, since it's obvious that any window width will introduce a time lag, it's just a question of how big a lag.
You might consider writing your own routine using a synmmetrical window.
A trick you can use with smoothing functions like this is to reduce the window size, run one smooth, reverse the data, run a second smooth. The second smooth undoes the shift created by the first smooth.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a suggestion for a symmetrical moving average window

The attached file is in P3 format, so your P2 will not be able to read it - therefor the pic.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a Savistsky-Golay filter (and a modified version of it that is marginally better). It is a pure convolution operation, and as such does not introduce a shift.
Also look up the ksmooth function, which uses a symmetrical kernel and therefore does not introduce a shift.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
super! the symmetric moving average works like a charm.
i'm looking at the savistky-golay versions as well.





