Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
solving ODE that consists of erfc(x)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
solving ODE that consists of erfc(x)
Dear all,
I'm trying to solve a PDE that consists of erfc(x) and exp(x^2) like the file attached below, which is simply a poisson's equation.
Since it has an unknown boundary condition, F electric field at position x=0, I tried 'minerr(F)' type resolution with F declared beforehand by initial guess.
Unfortunatlely, it keeps saying that F in the 'miners' syntax has not been defined.
Could anyone can help me?
Thank you in advance for your help.
Sung
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have a unit problem/inconsistency which makes the odesolve solve block fail, when called. Furthermore you should change the label of F in V(F):=... to "variable".
The meter in constant A should be to the power of 2, not to the power of 5, as they are now. Otherwise you can't add F^2 (under the root).
I am not sure what the error is, you made, but if I boldly add the required units to A
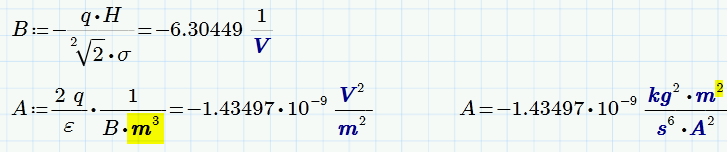
your sheet works OK:

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have a unit problem/inconsistency which makes the odesolve solve block fail, when called. Furthermore you should change the label of F in V(F):=... to "variable".
The meter in constant A should be to the power of 2, not to the power of 5, as they are now. Otherwise you can't add F^2 (under the root).
I am not sure what the error is, you made, but if I boldly add the required units to A
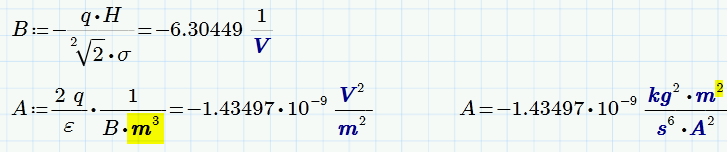
your sheet works OK:

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
It is my pleasure to have you again for this problem. I tried your tip and it works well.
In fact, I forgot to multiply N_{V} to the coefficient A that has a unit of m^{-3}.
Thank you very much for your keen observation.
Sungyeop
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
It seems solver work fine but, now, the problem is the value of V(d) which is unreasonably larger than 0.6 V (the boundary condition).
How can we make sure the boundary condition is fulfilled V(d) = 0.06 V, V(0) = 0?
Regards,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may want to have a look at your ODE as it seems that F has not much influence on the outcome:
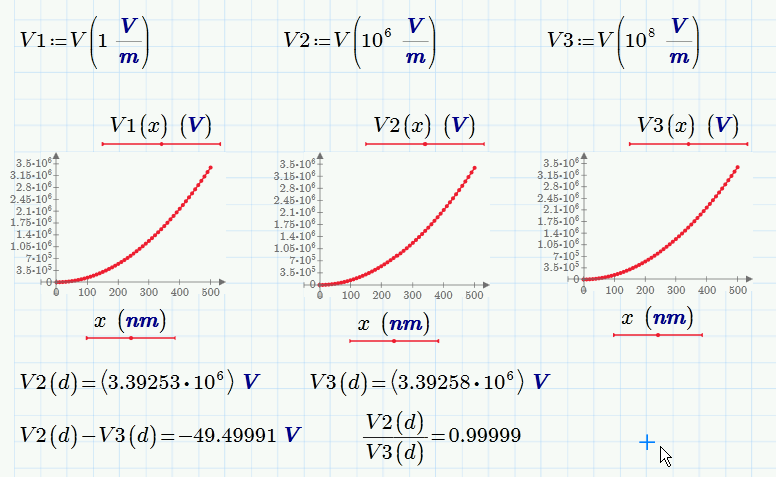
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What an inspring comment it was. I made a mistake in the polarity of the coefficients. Converting signs of A, B, C resulted in a good results.
Thank you very much Werner.
Sincerely,
Sungyeop





