testfirstname testlastname wrote:
See proof please:
Proof what?
"testxxxxname", what did you expect? You are using numerical math and therefore should be prepared for numerical round off errors.
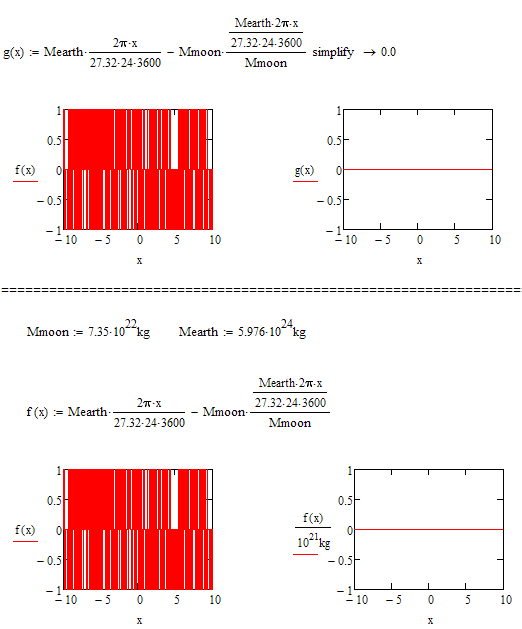
See attached that the error is just in the range of 10^-14 % - pretty good, I think.
See also two different ways to deal with the "problem", while the most obvious would be to cancel beforehand (I let Mathcads symbolics do the work) or apply some scaling.
testfirstname testlastname wrote:
no wish to change the display name?
But Mathcad can operate with much more numbers ( up to 10^307
Thats right (even more than 10^307, precisely 10^1024-1=1.797*10^308, its just Mathcads error message which mentions the 10^307), but that does not mean you will get a307 digit precision with your calculations. The range of numbers we can deal with does not say anything about the accuracy - it depends on how the overall bits are distributed on mantissa and exponent. More bits for mantissa - more accuracy but smaller magnitudes. But no matter how many bits you will reserve - calculations with "computer numbers" will be inaccurate.
So how to control accuracy? And how I know , that Mathcad suddenly generates mistakes?
You can't. You don't. Thats bad but if it would be that easy any program could correct its errors and produce 100% accurate results which is not possible. You as a user have to be aware of those effects and you may countersteer in some cases, like scaling down (or up) your numbers, etc.
In MC sometimes using the symbolic eval help, but its not applicable in any situation. Its hard to say when you will run into numerical errors (unless you follow the fatalistic way and accept it will happen anytime and anywhere). If you change the 1.1 to 1.2 in the following example you will get a difference of perfect 0.
The mathematical theory of numerical errors/numerical analysis is not an easy one and is closely related to the effect that the use of (inaccurate and usually truncated) measured data may have on the overall accuracy of a calculation. Sure not a trivial task to provide ranges the "real" (whatever that may be) result would be in with a certain probability, etc.
Numerical errors occur for different reasons, a finite set of numbers used with a finite precision, truncation errors (a sine is calculated by an infinite series expansion - it had to be truncated for obvious reasons), digitalisation errors (1.1 has just two digits in base 10, but an infinite number of digits in base 2 - its representation has to be truncated, unless you use something like BCD arithmetic).
Because the numbers used in computer arithmetic are so different (discrete, finite, ...) from the real numbers we usually think of, some simple mathematical laws we are used to do not apply. E.g. the commutative law of summation. As you can see in the example below, the order of the summands matters and influences (slightly in this case) the result.
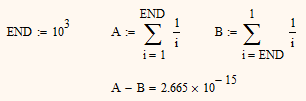
Sometimes people would come up with clever algorithms to overcome some single undesirable effects (e.g. Kahan summation algorithm), but in general you can be sure that computer arithmetic is not accurate and 100% precise - this applies to your clever pocket calculator, too 😉
How digits after decimal comma Mathcad takes to calculations? 17 ? Why not 307 ? How to control it?
You can set the result to DISPLAY up to 17 digits, which does not affect calculation precison. Why not 307 - guess because it would not make much sense to display that many (in most cases probably random) digits. Just because you see 100 decimal places does not mean the third one is still corect. Its always funny (and sad) to see students writing down all ten or twelve digits from their calculator display after calculations with measured data with a precison of just two decimal places. Thats some kind of lack of understanding, too.
If you really need to see more digits use symbolic eval (just up to 250, I think).
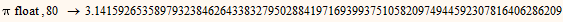
For small numbers you additionally can set the zero threshold from the default 15 up to 307. This will show you a result different from zero sometimes where you otherwise would just see 0. But there is no way to control the precision of calculation - Mathcads numeric will calculate the same in every case.
Thats a big difference to symbolic evaluation. If you use the keyword "float", the precison you indicate affects the whole calculation. Thats quite dangerous and therefor its usually adviseable not to use "float" in symbolic evals at all.
You may search the net for "numerical errors" "numerical anlysis", etc. for further reading.
