Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
unit^unit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
unit^unit
I know one problem with this

See also Mathcad PM (Prime Minister)
One semisolution
Mathcad 15

Mathcad Prime ![]()

Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery.
Valery Ochkov wrote:
Yes. My graph is a^b=constant. In Mathcad without units (m=1). Why? Mathcad cannot work with unit^unit.
Finally I can see that a^b = constant in the curve! But still non understanding why 😞 . You take L2 = ln(a)/ln(L1) with L1 in meters, so maybe have more complicated expressions for the units, even at the end must to be constant = m^m.
I never see something like your curve, but I'm not a curve expert. I guess that for the curve name Valery's curve isn't the best, just because you between hands have others like logarithmic or roth, in your math toolbar picture. Maybe the "potential - exponential Valery's curve" for this, and log-Valery's, root-Valery's for the "others". There are some math or geometrical institution where can ask about some antecedent of this?
Please, give us parametric expressions of the curve, and then eqs for arc length and area. Also, someone with a lot of ability and some time can construct the mechanical system showing in the plot. Your curve represent a geometrical system, with an amazing property, which can be translated to a mechanical system, and some other electrical via mec-elec equivalents (this is a circuit showing in an oscilloscope this curve).
Raise powers are curious. They are just a resumed products, that's easy, and seems to be the same than product is for the sum. But because is not a commutative binary operation (3^5 != 5^3) have to inverses: one by the right (roots) and other by the left (logs). And that's not that easy.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
Is there any physical or mathematical significance or use for this?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Hi Valery,
Is there any physical or mathematical significance or use for this?
Luc
Yes, there is!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
Hi Valery,
Is there any physical or mathematical significance or use for this?
Luc
See please No name curve

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I don't see any physical or mathematical significance here.
All I see is that you are violating the rules of exponentiation by using an exponent which is not a number.
AFAIK there is no definition in math or physics for hat kind of exponents.
Units in exponents simply don't make any sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
I don't see any physical or mathematical significance here.
Really?
This curve is a quartic plane curve defined as the set (or locus) of points in the plane such that the degree of the distances to two fixed points is constant.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This curve is a quartic plane curve defined as the set (or locus) of points in the plane such that the degree of the distances to two fixed points is constant.
The "degree of the distances" ???
I see what you have in mind.
But a +- b is defined and has a well defined dimension - length
a*b as well, its an area
a/b is dimensionless
but a^b simply is not defined, has not a well defined dimension and no physical or mathematical meaning.
What your graph shows is a^b=const. without any units for a and b as you had set m:=1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
This curve is a quartic plane curve defined as the set (or locus) of points in the plane such that the degree of the distances to two fixed points is constant.
The "degree of the distances" ???
I see what you have in mind.
But a +- b is defined and has a well defined dimension - length
a*b as well, its an area
a/b is dimensionless
but a^b simply is not defined, has not a well defined dimension and no physical or mathematical meaning.
What your graph shows is a^b=const. without any units for a and b as you had set m:=1.
Why not?
a +- b has dimension length
a*b - area or length*length
a/b - length/length
a^b - length^length
Yes. My graph is a^b=constant. In Mathcad without units (m=1). Why? Mathcad cannot work with unit^unit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ValeryOchkov написал(а):
a/b - length/length
Do you know this base Math constant?
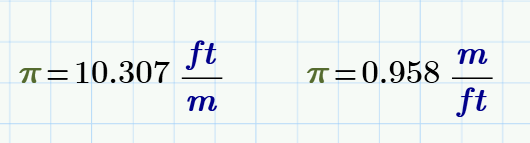
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, I can't see any reason why we should do so.
Unless I am missing the point, I guess you are departing from your own topic.
BTW, whats the correct result for (2m)^(3m) in your opinion? Whats the correct unit and what is the absolute measure, the number in front of the unit?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Mathcad cannot work with unit^unit.
For good reason. Mathcad knows about math and its definitions!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How do you propose to convert between units of length^length?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its even worse 😉
(4 m)^(2 m)= 4^(2m)*m^(2 m)=16^m * (m^2)^m
But (2m)^(4m) = 16^m * (m^4)^m
Is simply nonsense, as Victor already had written
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner.
In general, pow binary operation don't commute. So, maybe for pure numbers could be that 2^4 = 4^2, but this don't implies that must to be true for measures, like isn't Ln(a/b) = Ln(a) - Ln(b), which is true for pure real nonnegative numbers but false for measures.
Don´t think that this could be some strict. There are some others worst: ¿Por qué 5x3 no es lo mismo que 3x5? El problema matemático que se volvió viral - BBC Mundo . I don't have this article in english.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course I know that pow op is not commutative - the example was chosen on purpose to get the same number at the end.
The point was, that I would expect from a binary operation the same unit as an outcome, regardless of the numbers provided.
But in the first example we get number^m*(m^2)^m and in the second number^m*(m^4)^m. Thats quite different.
That was the point to show that it seems to make no sense using units in the exponent.
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner.
Sorry about saying that pow don't conmute, any collabs here don't need me to remember that, much less more you. You're true saying that have "not sense" regarding a^b where b have units. But for me the interesting point here is that meter^meter must to exist and have some sense, given that there are a curve with the property that two measured distances L1, L2 are related by L1^L2 = k. What's k? Not a magnitude, but must to be something related. So, I don't hope that magnitude's properties are preserves by power to the entity k, which I don't know what it is.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Units, for math programs, are those things that we want, or can do, to be.
My units package, for mathematica, now lives only in the web memorial cache, have been supersead by a built in one: http://webcache.googleusercontent.com/search?q=cache:RZrO5YR9MWUJ:library.wolfram.com/infocenter/MathSource/5511/+&cd=1&…
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure I understand what you're showing, but we both agree this is "simply nonsense."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hy Marks. That isn't. If 2^2 = 4 ft, that's don't mean that the unit for some "2" was in feet. You can get the correct values using mathcad as usual, but with nondimensional units.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
(16m)+(0.5m)=16.5m and (16ft)+(0.5ft)=16.5ft
(16m)*(0.5m)=8m^2 and (16ft)*(0.5ft)=8ft^2
do you suggest that:
(16m)^(0.5m)=4m^m and (16ft)^(0.5ft)=1.828706ft^ft ?
That means if we want to calculate this by hand we must first convert our length to meters (regardless of if we're using ft, mm, or any other unit length) and then convert the result into the units we want.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yep.
Well, that's short answer.
For long answer, we must to remember that in old books of phys and math there are always entire chapters about magnitudes. In those books demonstrates that given the newton's laws, there are a well defined entity called mass, which was a magnitude just because have a correspondence between plus and times operations, given the relationship m=a/F. In geometry I remember Puig Adams books, where there are a chapter called "Magnitudes" (magnitudes in english?) where define geometrically distances, and demonstrate the interception between circle and line without the algebraic theory of reals, adding an axiom to the Euclides ones.
Point is: Valery show us a curve with the property that L1^L2 = k, where L1, L2 are the distance to two fix points. Math programs refuses to consider magnitude^magnitude, meter^meter in this case. But, what about k? Is it a magnitude? Probably, not but must to be something. If you want to see the same properties as those for plus and times, must to prove first a closure property: magnitude^magnitude is a magnitude. And I guess that this isn't true.
For example, any superior limit of oscillation of real up bounded real valued successions are a real number (axioma de completitud o axioma del supremo). This property is a closure property. Other closure properties are Plus is closed in N, but not the inverse, minus, which is closed in Z. Product is closed in Z, but the inverse is closed in Q. Pow is not closed in Q, but closed in C, and with restrictions, in R. They two inverses too. Vectorial spaces have their own closure properties. Probability theory too. So, they are important.
If closure property don't holds, new things appear, with some unusual properties, like the limit for a succession of functions. Dirac's delta is the simplest example: isn't a function, and have some unusual new properties.
Old books each time that introduces a new magnitude, take some pages to prove that they are well defined magnitudes. With the correspondence for plus and times. So, I guess that meter^meter are not a magnitude, but, given that can show a geometrical origin for that, must to be something with sense. So, maybe can't preserve all the magnitudes properties, like "in system evaluation" (if all are in ft, the result is with algebra and in ft). Some thing happend when starting with Peano's axioms, want to preserve properties to the new entities, Z, Q, R, C. Between R and C, for example, lost some importants things, like order: can't preserve all.
Best regards.
Alvaro.
PD: To Werner: "degree of distances" are the words that a no native english speaker, like me and Valery, could use to say measured length.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alvaro!
I would like to write an article about this subject!
Would like you to be coauthor?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, that's go to be an honor to me! Thanks!
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery.
Valery Ochkov wrote:
Yes. My graph is a^b=constant. In Mathcad without units (m=1). Why? Mathcad cannot work with unit^unit.
Finally I can see that a^b = constant in the curve! But still non understanding why 😞 . You take L2 = ln(a)/ln(L1) with L1 in meters, so maybe have more complicated expressions for the units, even at the end must to be constant = m^m.
I never see something like your curve, but I'm not a curve expert. I guess that for the curve name Valery's curve isn't the best, just because you between hands have others like logarithmic or roth, in your math toolbar picture. Maybe the "potential - exponential Valery's curve" for this, and log-Valery's, root-Valery's for the "others". There are some math or geometrical institution where can ask about some antecedent of this?
Please, give us parametric expressions of the curve, and then eqs for arc length and area. Also, someone with a lot of ability and some time can construct the mechanical system showing in the plot. Your curve represent a geometrical system, with an amazing property, which can be translated to a mechanical system, and some other electrical via mec-elec equivalents (this is a circuit showing in an oscilloscope this curve).
Raise powers are curious. They are just a resumed products, that's easy, and seems to be the same than product is for the sum. But because is not a commutative binary operation (3^5 != 5^3) have to inverses: one by the right (roots) and other by the left (logs). And that's not that easy.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BTW, I get a different looking curve when using your values.
See here -> Re: No name curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Added an animation for Valery
Looking forward for Valery providing the parametric equations and equations for arc length and area, as Alvaro demanded ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner. You're looking me some sadic. Well, for this case maybe you aren't wrong. Have not idea about how difficult could be get the parameterization from the expressions that are obtained with the solve for x,y in the Valery's worksheet, but they looks enough complicated for play with that a couple of weeks or months and don't get any good expression. Maple have some functions to do that, but don't know how powerful could be them. But they must to exist, and someone can get them; difficult is know when. At least, you can't add a diabolic tail to me: I don't ask for polar expressions.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz написал(а):
Hi Werner. You're looking me some sadic.
Best regards.
Alvaro.
Sadistic - sádico? ![]()
Sorry - for me too. See other example Re: One catenary problem
May be I am a Math-m a s o c h I s t.
PS
One joke.
In Moscow, police broke up a demonstration of masochists. Both sides have been enjoying.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11 gives the correct answer
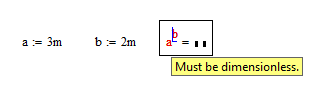
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, it is not correct answer!
Maple gives the correct answer:






