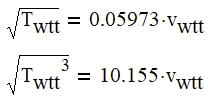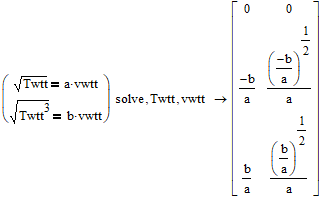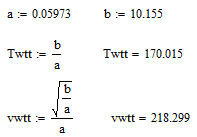units in a given/find block

[AF_9801489]

Hello Ladies and Gents, 

solving a non-linear system of equs.

Assigning the output values (there are 2 variables but the solution shows 6 output values) to the variables, the units disappear.

Script enclosed. 

Please advice.

Thank you. 

Arturo

[Werner_E]

OK, lets start with the fact that you see 6 output values. Actually what you see are three sets of solutions. Each of the three columns represent a solution. The first one being T.wtt=v.wtt=0. The second one obviously the one you are looking for and the last one using a non-real value.

You used the symbolic evaluation and this usually tries to find all solutions. Furthermore the symbolic does not know anything about units (it treats them as unknown variables). In your case the symbolic does not see any units, because the symbolic use of "Find" does not need and doess not use any guess values.

All the symbolic sees are the two equations in two variables and there are no units:

In your case it sure would be better to use the numeric evaluation, which gives you a solution which may depend on the guess values. But before you go ahead doing so, you will have to make your equations unit balanced.

As you have it now, in the first equation the dimension on the left hand side is root of temperature, while the dimension on the right hand side is velocity. Mathcad will complain about that. Similar you second equation is not unit balanced either.

So you have two choices:

1) strip all units (here in the guess values) and add the corrrect units to the result

2) make the equations correctly unit balanced - probably by adding units to the factors.

Here is one way for option 2, hope it makes sense

[LucMeekes]

It's a wonder you get an answer at all.

With two equations, you can only get a unique solution for (at maximum) 2 variables.

Then your units don't balance:

If the square root of Twtt has the same unit vwtt, then the square root of the third power of Twtt cannot have that same unit.

Conclusion: You're working with empirical equations. You should divide the units out (or use the UnitsOf function).

You're also far better off with solving the set symbolically:

Shows there are three possible solutions, two of which will probably be useless, or physically impossible.

Pick the right one (the third) and fill in the values for a (=0.05973) and b(=10.155):

Success!
Luc