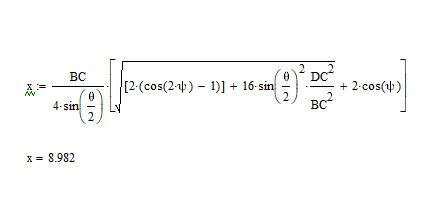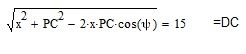Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
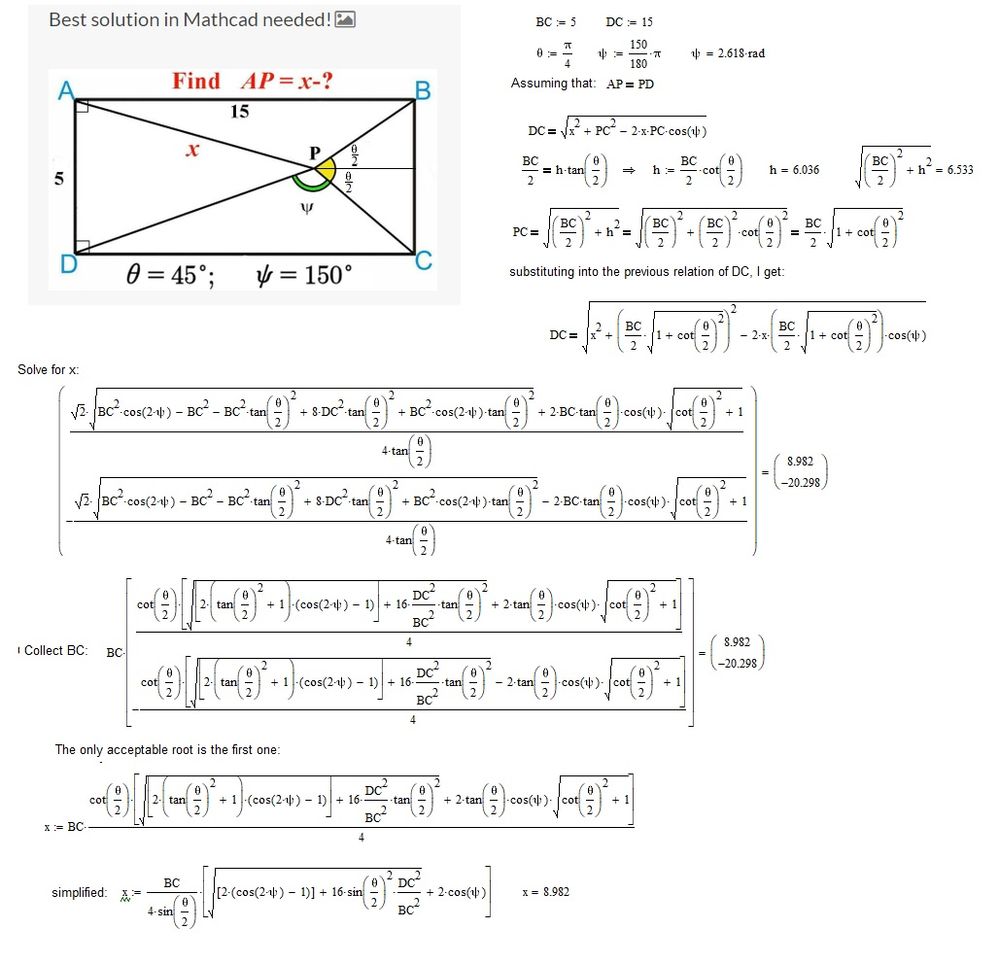
Best solution in Mathcad needed!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No answer - that's a pity!
But no matter - anyway, to conclude for what ever it may be worth, here is a small animation made a few days ago, which shows the position of the possible solutions for P and the graphs of the distance functions at variable distance CD.
have fun!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
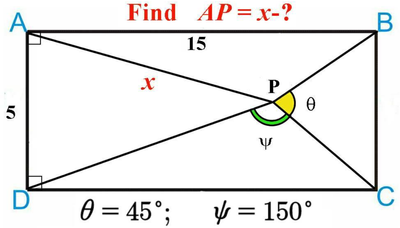
Hi Valery,
to me it is x=8.982
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
Hi Valery,
to me it is x=8.982
There is a discrepancy to my solution.
But if my guess is correct Valery already has a solution in his hand and he can tell which one matches.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Best solution in Mathcad needed!
What is "best" ?
"best" may be the simplest way to get the solution (simple is also hard to define), "best" can mean the the most visual solution or it can be the solution you already have in your drawer to post it later.
"best" can also mean the shortest solution and this would be to just type in the correct expression (if you are after an exact result) or the number like this:
![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
????
Your reply is an empty post???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I wanted to delete it, but I can't, I can't find the right instruction.
As a test I used Carnot's theorem :
PC is necessarily the side of an equilateral triangle with base, BC.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
I wanted to delete it, but I can't, I can't find the right instruction.
Silly as it is but we are not allowed to delete our posts, but we are allowed to edit them even when somebody already answered to this post an may have referenced it. Thats not really clever.
As a test I used Cartesio's theorem :
Guess you are talking about the Law of cosine (cosine rule, Al-Kashi's theorem) for triangles in Euclidean geometry. https://it.wikipedia.org/wiki/Teorema_del_coseno
I used it, too. Another way would be to intersect two circle arcs.
PC is necessarily the side of an equilateral triangle with base, BC.
I don't see that symmetry. The distances from P to the four corners of the rectangle are all different.
As far as I see it the triangle BCP is neither equilateral nor isosceles.
Why do you think that PB=PC ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
According to my intuition, the theta angle is 45 degrees and it is so only if PB = PC otherwise it assumes different values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
According to my intuition, the theta angle is 45 degrees and it is so only if PB = PC otherwise it assumes different values.
Your intuition is deceiving you 😉
There are a lot of different triangles with base BC and angle 45 degree at P. All possible locations of P are on a circle. I don't know what its called in English, in German its "Peripheriewinkelbogen". I doubt that Google translate does correct with "Peripheral angle arc" or "Peripheral angle circle".
See my picture which I added to the post above for the solution which clearly shows the different lengths.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right on the circle. What I'm not sure of is that both angles remain constant moving P on a fixed circumference. However, my solution is not wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, but what you show at the bottom right as a "proof" is no proof because you again use the wrong assumption PB=PC here.
Calculate the coordinates of P with your "solution" and then calculate the lengths and angles one by one without assuming any symmetry (which simply isn't there).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
you are right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just noticed that an easy way to see that is when you try to add up the four angles you calculated - they should add up to 360 degree but they don't.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I apologize, you are right. Ich bitte um entschuldigung!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
I apologize, you are right.
Absolutely no reason to apologize for a mistake that can happen to anyone.
In fact I wasn't absolutely sure about my solution which was developed rather quick (and dirty) but after I checked with the angles as shown in the picture above as a consequence of our discussion, I feel pretty sure now.
Maybe you find the time to solve, too, and confirm.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Genau jetzt habe Ich diese solution gefunde, was glaubest du daruber?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its hard and boring to debug just a pic, but as far as I see you have five unknowns to solve for but only 4 equations. This would mean that there would be an infinite number of solutions and the searched for solution would be amongst them, but is not necessarily the one Mathcad solve block comes up with.
BTW, are you sure that those 4 equations are independent from each other? If they are not, additional degrees of freedom comes into play.
Do you get different results if you change the guess values, lets say x:10 for example?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just to be on the safe side I solved the problem with a completely different approach compared to my first (P as intersection point of two circles as mentioned in one of my replies above) and got the very same result as with my fist method. So I assume its the correct result.
EDIT: This second approach can be significantly simplified as we already know one of the two points of intersection (B in my nomenclature). Therefore we only need to mirror B at the connecting line of the two circle centers to get P.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here I added the condition that the sum of the areas of the single triangles is equal to that of the rectangle:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So you see that changing the guess value changes the result significantly.
Using your method you can get a myriad of different "solution" but only one of them is the correct one. Unless you add additional appropriate constraints your solve block will hardly find the correct one only.
The 5 equations you have so far are not independent!
If two of the four lengths x,y,z,t are given, the other two can be already calculated.
I just posted a different approach and again arrive at the solution I found first. So I guess we can assume that this is the correct one 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I approached the problem in three different ways and also tried to derive a symbolic solution from each.
Its interesting to see the different ways Mathcads symbolic is able to display the result when asked to simplify.
Mathcad 15 file attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Numeric solution from Pythagoras, Hero and... Valery
I have a dream - to write a problem book for school, when the problem in mathematics, physics, chemistry, etc. is solved hybridly - by attracting the student’s head and mathematical packages. Who wants to help me!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Numeric solution from Pythagoras, Hero and... Valery
So Heron is your hero ? 😄
Your approach is very similar to what Francesco came up with - he just used other formulas for the triangle areas. As your attempt shows, it looks like the four equations stemming from the cosine law are independent (so my guess that Francesco's wrong result is because of still dependent equations was wrong).
I had another look at his last approach and I think he got a wrong result with his last try where he added the comparison of the areas because he used sin(delta) with a wrong, fixed value for delta in the solve block.
Probably he will get the correct result when he replaces sin(delta) by sin(2pi-alpha-beta-gamma0) or by sin(phi-gamma0) as it seems that he had defined phi:=2pi-alpha-beta somewhere outside of the picture he posted.
Can you provide a symbolic solution using your approach or at least an exact numeric one (with roots, etc.)?
In real Mathcad we can evaluate a solve block also symbolical and for reasons beyond me your solve block returns non real values if I try.
The symbolics switches into float-mode and returns those useless non-real numbers. If I add the constraint AP>0 nothing changes, if I add AP>1 the solve block fails 😞
Any ideas whats going on and how to get a symbolic result with your approach, too?
BTW, if I put your five equations in a vector and use the symbolic "solve" command, then no solution is found.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My take on the numerical solution. Nothing very different I think.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We are opening an auction! Starting price - 18 unknown! Who will give more! 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
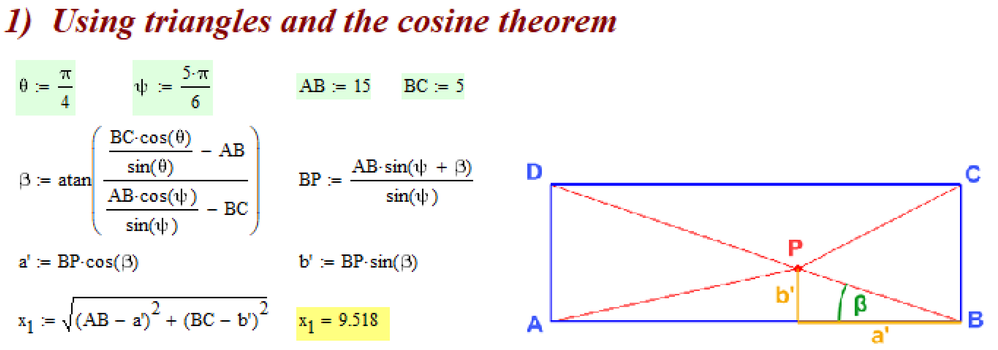
OK, here is the approach which came into my mind at first.
Its basically the way a school pupil would be assumed to approach the problem. BP can be expressed in two ways using the triangles ABP and BCP using an auxiliary angle like beta in my pic. From the resulting two equations I eliminated BP and using the basic angle sum and difference identities I arrived at an expression for beta. Mathcads symbolics wasn't of much help here and it was quicker done by hand 😉
Using beta we can calculate AP and then the position/coordinates of P (using a' and b') and finally the distance x=PD.
The approach is straightforward, we get a nice (but not fully simplified) exact result and the approach can also be done fully symbolically (see one of my previous posts with all the symbolic expressions -> x1)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And now my second approach.
It follows the way one would draw a sketch of the situation using peripheral angle arcs. Not sure whats it really called in English - maybe a native speaker could help.
Its quite easy to determine the center and radii of the two circles and using the symbolic solve, the points of intersection are found. Of course one of those points is B, so we filter for y>0 (and surprisingly Mathcads symbolics really takes this condition into consideration) to find P and finally calculate x=DP.
Again we can also get an exact result (not fully simplified and equivalent to, but more complex as the expression we got with method 1).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
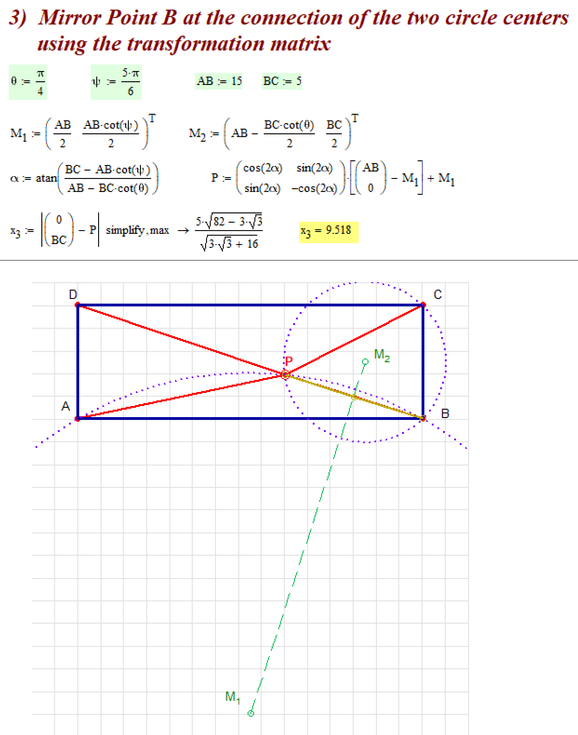
Finally my last approach and the worksheet.
After thinking about method 2 where we intersect two circles and already know one of the points of intersection, it was clear, that all that must be done is to mirror this known point B at the connection line of the two circle centers.
This sure could be done in quite some different ways and I settled at using a transformation(mirroring) matrix.
This approach delivers the most simple exact representation of the result as could already be seen in the sheet with the symbolic functions I posted a while ago. -> x3
x3b was an attempt to manually simplify the expression further, but while the symbolic expression looks a bit smaller, the exact result with the values provided could not be simplified by Mathcad in a satisfactory way.
Here is the picture of method 3 along with a plot showing the circles and also the mirroring of point B to get P.
MC15 worksheet attached.