Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Community
- Creo+ and Creo Parametric
- 3D Part & Assembly Design
- wavy circle by equation
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
wavy circle by equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
wavy circle by equation
Hi all, I have been trying to figure out how one might create a 'wavy circle' similar to the attached screen shot by using curve equation. It is 2 dimensional.
Regards
John
Solved! Go to Solution.
- Labels:
-
Surfacing
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
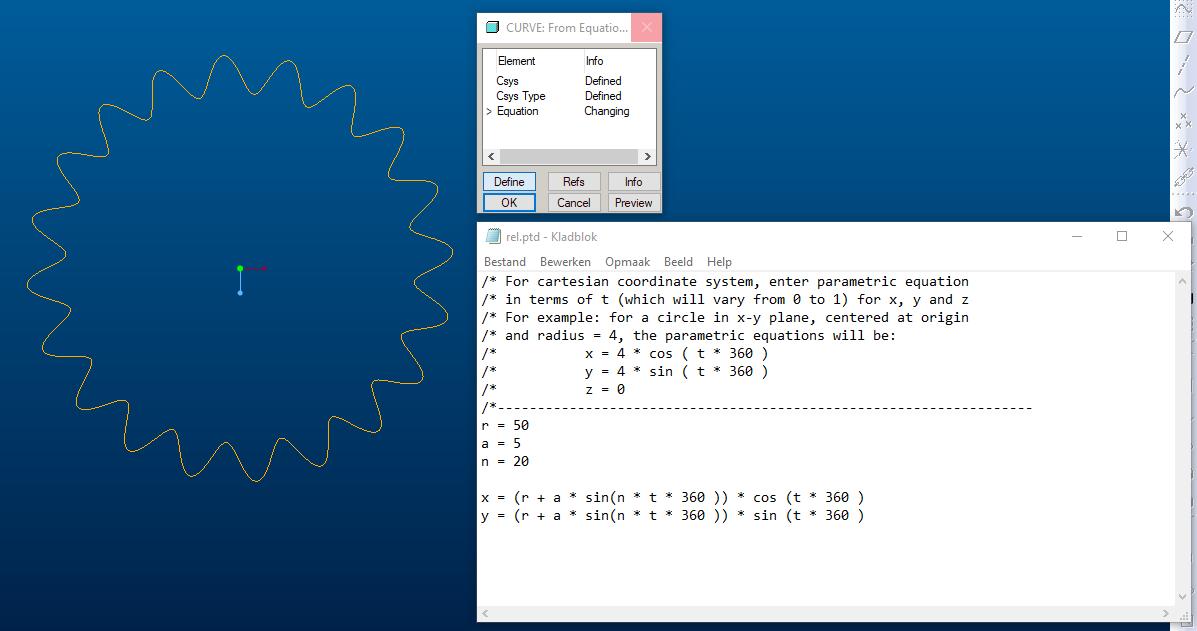
/* For cartesian coordinate system, enter parametric equation
/* in terms of t (which will vary from 0 to 1) for x, y and z
/* For example: for a circle in x-y plane, centered at origin
/* and radius = 4, the parametric equations will be:
/* x = 4 * cos ( t * 360 )
/* y = 4 * sin ( t * 360 )
/* z = 0
/*-------------------------------------------------------------------
r = 50
a = 5
n = 20
x = (r + a * sin(n * t * 360 )) * cos (t * 360 )
y = (r + a * sin(n * t * 360 )) * sin (t * 360 )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
/* For cartesian coordinate system, enter parametric equation
/* in terms of t (which will vary from 0 to 1) for x, y and z
/* For example: for a circle in x-y plane, centered at origin
/* and radius = 4, the parametric equations will be:
/* x = 4 * cos ( t * 360 )
/* y = 4 * sin ( t * 360 )
/* z = 0
/*-------------------------------------------------------------------
r = 50
a = 5
n = 20
x = (r + a * sin(n * t * 360 )) * cos (t * 360 )
y = (r + a * sin(n * t * 360 )) * sin (t * 360 )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, I knew there would be an equation. I just could not figure out how to introduce number of cycles & amplitude to a circle in x-y plane.
Best regards
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the first time I have created such a curve.
I combined the knowledge from the reply by Max in this StackExchange post "Equation of sine wave around a circle" with this Creo post about Equations for Curves and more.
After I replaced "θ" (the angle) with "t * 360", the wavy circle showed up.