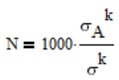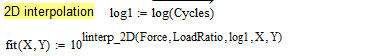Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
2d linear interpolation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2d linear interpolation
Dear all,
I'm facing again a problem with linear 2D interpolation.
In this case I tried to see if the results of direct and inverse interpolation coincide.
z=f(x,y) and y=f(x,z).
Unfortunately, they don't.
Could you please help me in finding the solution of this problem?
Attached you see the mathcad file.
Thank-you very much for your support.
Regards.
Enrico
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
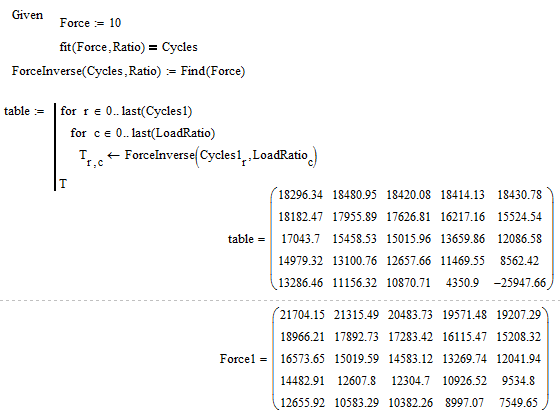
Sorry, but I see no reason why the two diagrams in your sheet should coincide.
Your first table yields a value for cycles of 35309 if force=16574 and ratio=0.2.
Your second table suggest a cycle value of just 100 for the same values. Obviously different functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
Thank-you very much for your reply.
You are right. I've sorted out the file. Now it should be clearer.
I still find some difficulties by interpolating the data.
I really appreciate your support!
Regards.
Enrico
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just looked at the top of your new sheet and compared the "inverse function" you provide (Force1) with the inverse values we can calculate from the given data (Force, Cycles, LoadRatio) using a solve block to provide the inverse function.
Some values are similar, some are quite off. So its no surprise that you don't get the same results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
Why are there value which do not correspond?
Is that due to the fit function you use to provide the inverse function?
below you find the function.
In the direct function I calculate the "N" while in the inverse function I calculate sigma.
The tables from excel are correct. Why shouldn't not work with mathcad?
Thank-you very much for your support!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why are there value which do not correspond?
Is that due to the fit function you use to provide the inverse function?
I'm not sure, but it looks like the two data sets don't stem from the same function.
Don't think that the interpolation is responsible for the big differences.
Why are there value which do not correspond?Is that due to the fit function you use to provide the inverse function?
below you find the function.
"log" means logarithm to base 10 as in Mathcad?
sigma is Force in your sheet, N is Cycles, k is LoadRatio ?
Whats the value of sigma.A?
BTW, If you have a function, why would you need interpolation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
The data sets stem from the same function. You can prove it observing the two excel tables I've copied on the right side of the mathcad sheet.
Below the answers to your questions:
"log" means logarithm to base 10 as in Mathcad? Yes
sigma is Force in your sheet, Yes
N is Cycles, Yes
k is LoadRatio ? No, each column of the table "direct function" is a S-N curve obtained for one specific load ratio.
The load ratio is defined as (Fmin/Fmax). "k" is the slope of the S-N line and changes with the load ratio.
Whats the value of sigma.A? SigmaA is the force corresponding to 1000 cycles and varies for each load ratio.
I need the interpolation to get the function N=f(Force,LoadRatio).
The equation I wrote down indicates the relation between Force and Cycles: Cycles=f(Force).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, I was asking because I was curious if i would be able to calculate and so verify the data tables you provided myself. But obviously I don't have enough information to do so.
I have looked at your Excel table pictures and I noticed that the red underlaid values fit pretty well, but the yellow ones don't!
With Ratio=0,8 and Force=10000, the first table shows cycles=285792
With Ratio=0,8 and Force=10926, the second table shows cycles=100000
This discrepancy may be possible, but may also be a sign the the data tables don't match up.
I can't tell as I am not able to recalculate the data in your two tables.
So the reason for the values not being the same may either be an error in one or both of your data tables, or it can be because your data values are too far apart and linear interpolation is not appropriate - can't decide.
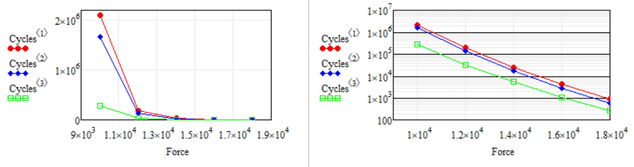
BTW, you write that k is the slope of one column in your first data table but when I look at hos curves, they don't seem to be perfect straight lines with a constant slope - not in linear, nor in log scale:
I need the interpolation to get the function N=f(Force,LoadRatio).
If you have a way to calculate k for a given Ratio, wouldn't it be simply
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Werner,
The discrepancies are possible since a low variation of the stress can lead to a big variation of the number of cycles.
The S-N curves are linear if x- and y-axis are logarithmic.
I think that the data are too much apart from each other for linear interpolation.
I tried also the following interpolation
which is working better for low number of cycles but poor for high number of cycles.
Do you have any idea how I can deal with this issue?
Thank-you very much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you have any idea how I can deal with this issue?
Unfortunately - no.
I tried with a modified interpolation function which would use logs only when interpolating the columns, but to no avail. The result was the very same is you have in our last sheet.