We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
2nd Moments of Area
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2nd Moments of Area
Hello to all!
Tonight I am working on what should be a simple problem as below:
I know that from my reading material I have been given that:
So for my simple triangle problem I have started by defining y (assuming that y is symmetric about x as:
I have then integrated using the given forumula for JT but I am not coming up with the model answer of 1/48*B^3*H I am instead getting H to the power of 4? Which is a reoccurring problem...
Following the question I have used the same approach for JoL and JL given that these are defined as:
NB JL is the only answer I get spot on but only by using the given answer for JoL not the one I have calculated.
Further if anyone can elaborate as to how J1L would be derived for a base of x=H? The given answer seems to be the answer for JoL for a rectangular shape?
As always your help is greatly appreciated.
Andy
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

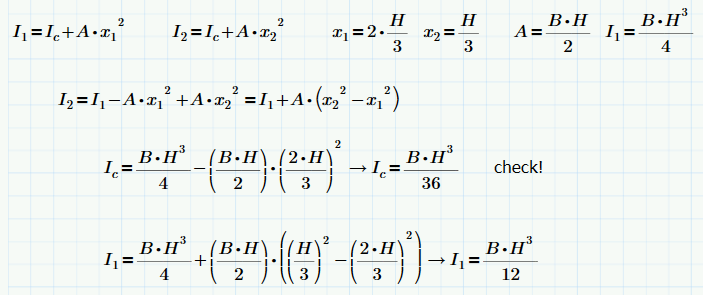
The moment of inertia about the centroid is always the smallest! You can translate between any two if you do the math right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andy Wibroe wrote:
I have started by defining y (assuming that y is symmetric about x as:
Take another look at your definition of y
Give some values to H & B and check a few values of x & y.
For example, if we assume H=10 and B=8, let's check what you get for y when x=5
y = B * x / 2 = (8) * (5) / 2 = 20
Is this a reasonable value for y?
I'll give you a clue: the equation for y needs to include the variable H.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Eureka!
I had omitted the H
So this should be:
This gives the correct answer for the first three 2nd moments.
Any idea on the derivation of the last? i.e. J1L?
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
That is amazing! Thanks so much!
Is it however, possible to set up in the way I was doing originally i.e. integrating over one half of the triangle and multiplying by 2 noting the triangle is symmetric about x?
Thanks,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The calculation of centroid locations will not work with your technique (in the y direction) because the figure is symmetrical in y.
In general, the answer is "No".
I use this technique on airfoils shapes, defining the y(x) for the top and bottom surfaces, so it works in general as a computed numeric solver. The expressions from the symbolic solver are specific to the triangle figure.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Thanks again, I understand what you are saying. I have tried to stick with the method I was using as best I can as I believe this is the method that is expected of me. But I do understand fully the logic of not relying on symmetry about x and integrating between -y to +y.
I have however managed to rearrange as follow:
What I find perplexing is that taking what is essentially a second moment about the distance x from x=0 from the second moment of the total area gives the second moment about the new point x. This I have proven above with the calculations of JL which work either by integration and with the subtraction method. However, this does not seem to work for JL1. i.e. JL1 can be derived by integration but not by the subtraction method. Why is this?
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

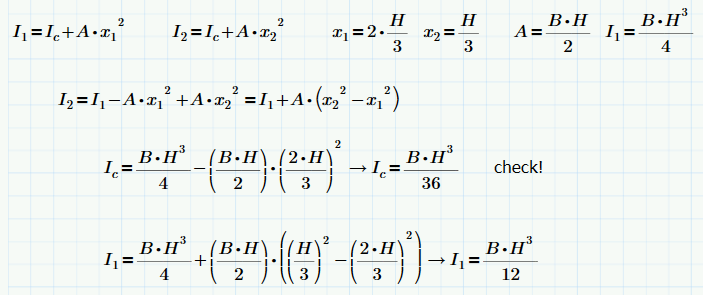
The moment of inertia about the centroid is always the smallest! You can translate between any two if you do the math right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Andy, the "subtraction method" that you reference is really just the reverse of Fred's first equation here:
Note that JL is the moment of inertia about the centroid, or I.o in Fred's equation.
If you want to solve for J1L using this method, use the following:
JL = J1L - A*(x')^2
or
J1L = JL + A*(x')^2
Where x' is the distance from the centriod to the new axis: x' = H - x.bar = H - (2*H/3)
This is exactly what Fred is showing. I just wanted to make sure you saw the correlation between his variables and yours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Both,
My sincerest thanks. Really helpful explanations for my continued learning!
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One question, why can't the Ishift be calculated directly from the total 2nd moment about x=0? in the same way that JL ie 2nd moment about centroid can?
You cannot go from x = 0 directly to x = H because you're crossing the centroid position and the x in the equation I = I+A*x^2 is calculated incorrectly. If I plot moment as a function of position I get:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Cheers Fred,
In the example above, Iwe have looked at a position further from the centroid from x=0.If I wanted to find moment about a position between x=0 and the centroid I assume I would still work from the centroid but would this still be of form Ishift=Io+A(x)^2 or would this now be Ishift=Io-A(x)^2 as I am working back toward x=0?
Cheers,
Andy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The moment of inertia thru the centroid is always the smallest you will calculate along that axis. The moment calculated about any other point must be larger. So the moment of inertia increases no matter which way you move from the centroid, and I = Io + A x^2
I >Io whether x is positive or negative
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK so the crux of the problem is find the second moment about the centroid then you can find the 2nd moment about any point by adding A(x')^2 to the centroid where x' is the distance either direction to the new point?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You got it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is the right way to think about this problem.
However, if you happen to know the moment of inertia about an axis other than the centroid, and you also know the distance from that axis to the centroid, then you can use this knowledge to back-calculate the 2nd moment about the centroid (the "subtraction method" you described above).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I suppose you can directly calculate one from the other as long as you know the difference in distance from the centroid to each axis (including +/-).
If x1 is x' units further from the centroid than x0, then Ix1 = Ix0 + A*(x')^2
If x1 is x' units closer to the centroid than x0, then Ix1 = Ix0 - A*(x')^2
Using the originally posted question:
x=H is closer to the centroid than x=0 by a distance of H/3
Therefore, the following should be true:
J1L = J0L - A*(H/3)^2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the original question surely x=H is further from the centroid than x=0 i.e. from left to right long x you would come across x=0 then H/2 units later the centroid then H/3 unis later x=H which is why I origonaly thougth you could derive from LJ1=LJ0+A(x')^2. where x' is H?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The centroid is at x=2H/3.
Therefore, the distance from x=0 to the centroid is 2H/3, and the distance from x=H to the centroid is H/3.
That means x=H is closer to the centroid than x=0 by a distance of H/3.
OK so the crux of the problem is find the second moment about the centroid then you can find the 2nd moment about any point by adding A(x')^2 to the centroid where x' is the distance either direction to the new point?
This comment is the best way to think about the problem. My response to Fred was to answer his question, but it is more confusing to try to think of the problem the way I framed it there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The centroid is not x = H/2, it's x =2H/3.
The distance from x =0 is 2H/3, the distance from x = H is H/3
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yyou guys know your stuff!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, they definitely do! Just like custom writers from handamdewritings custom essay writing service!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Andy!
Your problem is a good exercise and example for multiple integration of functions, i'm teaching my students.
The interrestig there is the relationship between the Steiner-moment and the directly integration.
You can see an example in the attachement.
Best Regards, Volker







