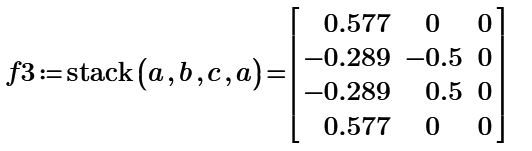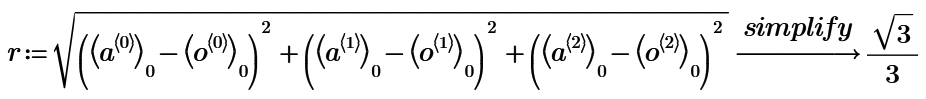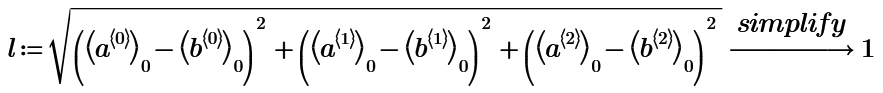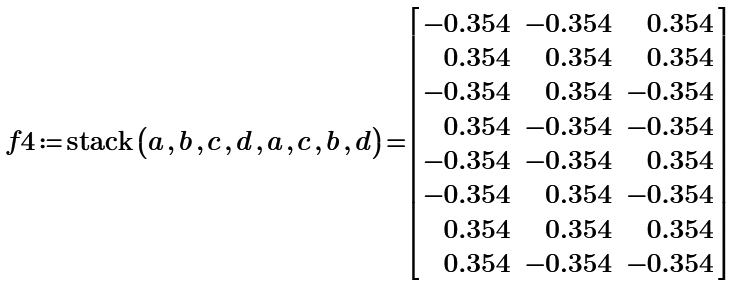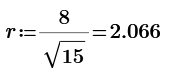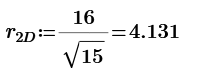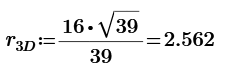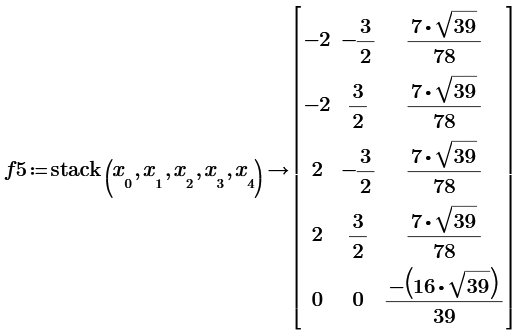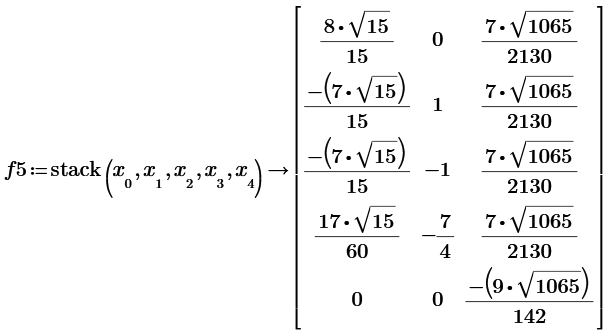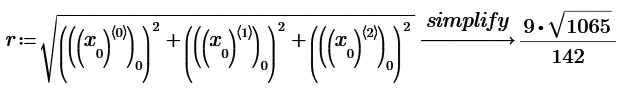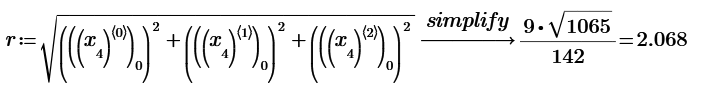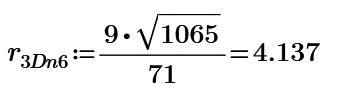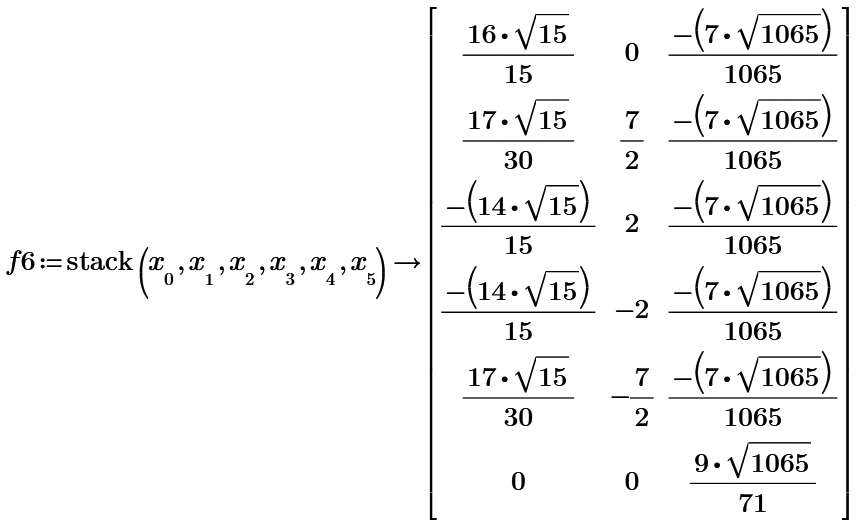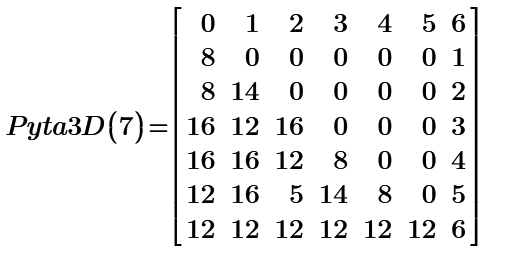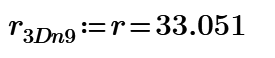Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
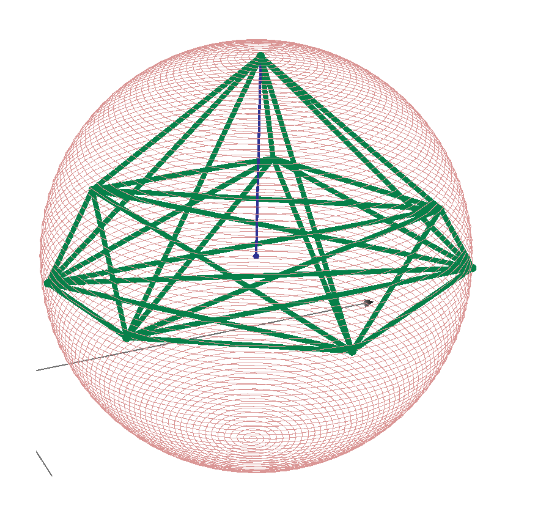
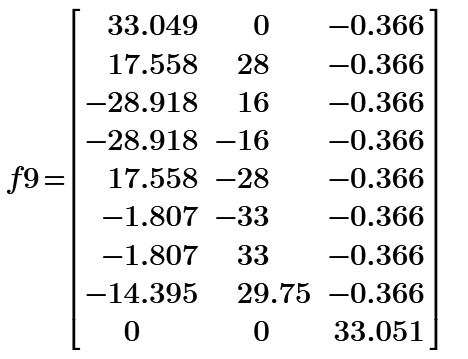
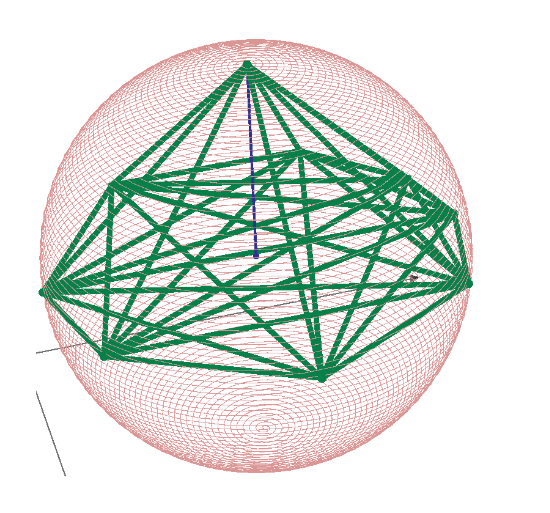
All distances of the points on the sphere to be Integer
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All distances of the points on the sphere to be Integer
All distances of the points on the sphere to be Integer
n=2, r=0.5, l=1 (0.5,0,0),(-0,5,0,0)
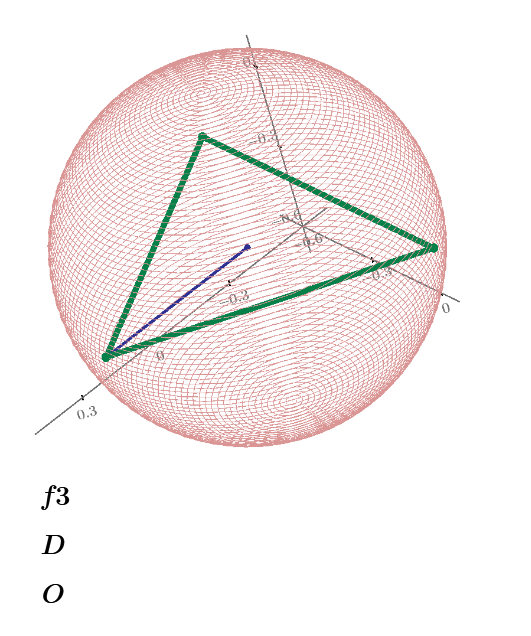
n=3,
- Labels:
-
Puzzles Games
- Tags:
- Prime_6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
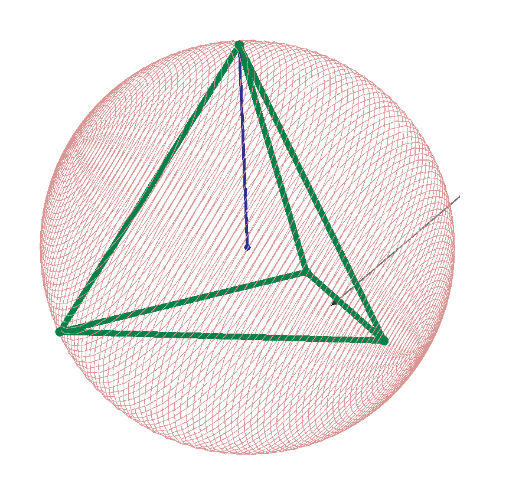
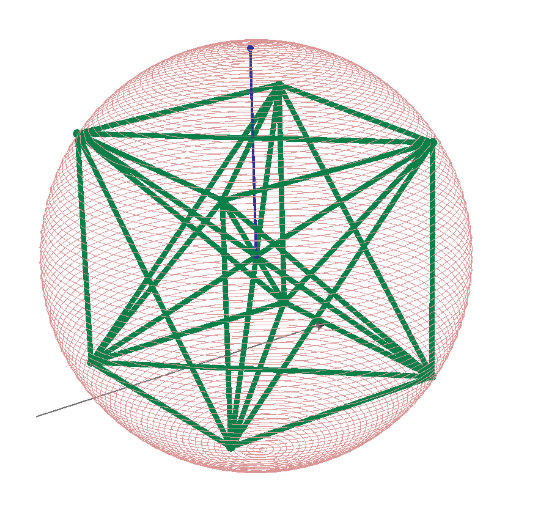
n=4
How about other points n>4?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
n=4 of 2D;
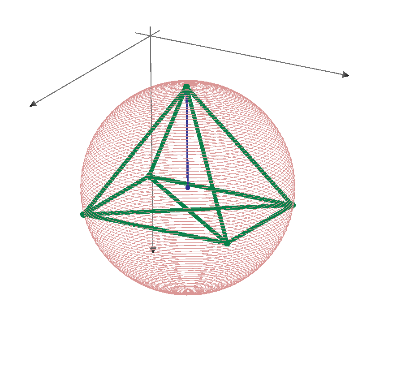
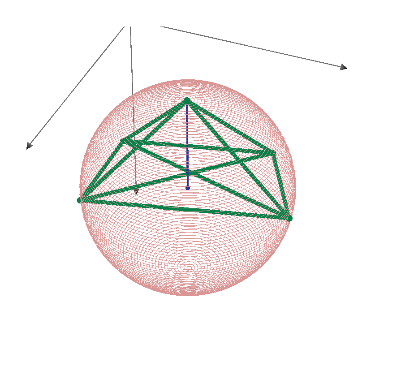
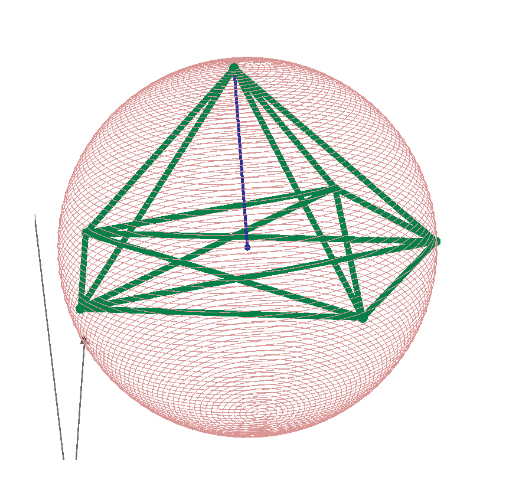
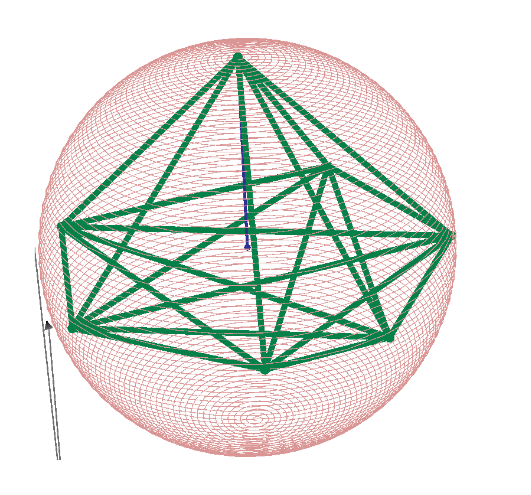
The one of 3D;
n=5 of 2D; by terryhendicott
The one of 3D;
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
n=5 with new 2D n=4 results.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
n=6, r2D6p=
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime_6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
All distances of the points on the sphere to be Integer
n=2, r=0.5, l=1 (0.5,0,0),(-0,5,0,0)
n=3,
The problem of the precise number that lies on the surface is of a number theoretic nature. It has to do with the number of ways we can express an integer as the sum of n squares. A lot of modern and classical work in number theory relates to this question.
The other problem, where we count all the points inside instead of just those on the boundary, is of a different flavour. If ar denotes the number of lattice points on the surface of the 3-d sphere with radius r centered at the origin, then each individual ar fluctuates quite erratically. If we study the sum a1+a2+⋯+ar instead, then we get smoother behavior and analytic methods can be applied.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks to reply my subject.
Solved: All distances of the points to be Integer - PTC Community
Above is the one of 2D. I am solving the n points answer for both 2D and 3D.
If you know any study corresponds these puzzles, please let me know it.
Tokoro.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is not the answer of n=8.

- Tags:
- puzzle