Community Tip - You can change your system assigned username to something more personal in your community settings. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Array Dimensions Do Not Match
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Array Dimensions Do Not Match
I'm attempting to do a simple matrix subtraction operation and it doesn't appear to work.
I just get the "Array Dimensions Do Not Match" error however as shown in the attachment, the dimensions clearly match.
Not sure if it has anything to do with one matrix have double parentheses (not sure why as I didn't intentionally creat this) and the other having single.
In any case, I've attempted multiple things including using the Vectorise but this doesn't resolve it.
Any assistance greatly appreciated.
Thanks.
Wade
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks like the first is just a 1 x 1 array with a 2006 x 1 vector as its element, while the second is a normal 2006 x 1 matrix.
Try to use the matrix index 1 when you use the first.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks like the first is just a 1 x 1 array with a 2006 x 1 vector as its element, while the second is a normal 2006 x 1 matrix.
Try to use the matrix index 1 when you use the first.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"Not sure if it has anything to do with one matrix have double parentheses (not sure why as I didn't intentionally creat this) and the other having single."
It does.
The double parenthesis means that you have a matrix (or vector) as an element of a matrix (or vector). This is a.o. what you do with matrices
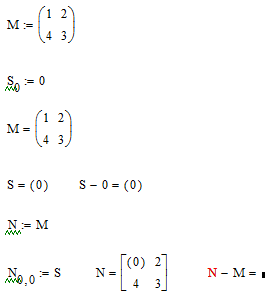
Without your worksheet it's a little hard to understand why you got the nested vector, but the non-vectorized expression could be the cause.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your responses.
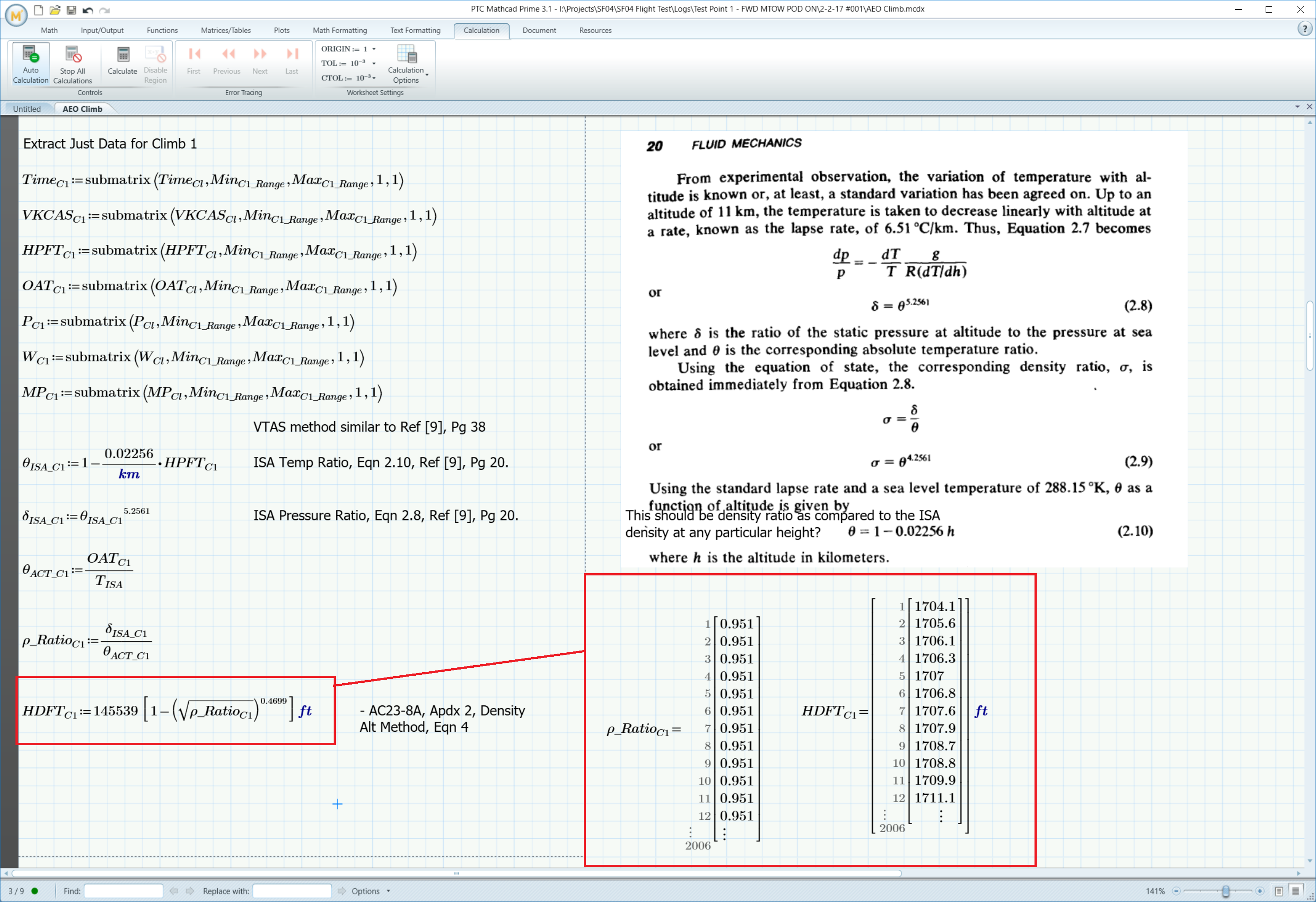
I've included an image below of where this occurs.
What I want was the equation to perform the operations to every element in the density ratio matrix which it appears that it has, just that the result gets put in as a separate element vector within a 1x1 vector rather than just the vector by itself.
Do you have any advice of how I might modify the original equation to get the result I need (i.e. just the single vector)?
Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looks like the solution is the break each section into separate terms the add / multiply the terms together at the end.
Thanks again for your assistance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As it is now, the HDFT vector is nested vector: A vector where one or more of the elements are vectors. In this case HDFT appears to be a 1-element vector, where the one element is a vector in itself.
Werner suggested, as a work-around, to take that vector out, by doing HDFT[0.
Ideally you should prevent to get the nested vector at all. I can't exctly predict from your pictures what causes it to become nested.
If you want more detailed help, we need the worksheet, not a picture of it.
Success!
Luc





