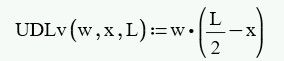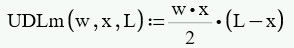Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Custom Function - ignoring matrix variable...?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Custom Function - ignoring matrix variable...?
I have a MathCAD Prime 7.0 worksheet and I created three custom functions, which are very similar.
The each seem to process variables somewhat correctly, but only one of the three will process a matrix/range variable even though I've tried using the same arguments for all three.
Any idea why the two later functions are treating the matrix/range variable as a constant?
Thanks!
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
-
Programming
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks @terryhendicott !
I'm just getting back into working with MathCAD after a few years hiatus...
Just for my own knowledge...why was the one function working okay without vectorization and the others weren't?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
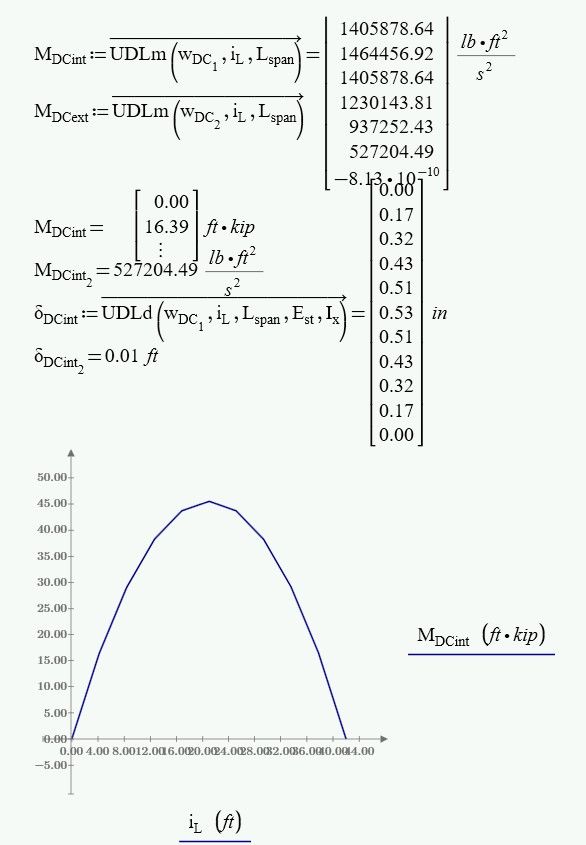
On contrary to UDLv, your function UDLm calculates the product x*(L-x) and if x is a vector, then this is the product of two vectors and Prime correctly returns the dot (scalar) product and thats a scalar and not a vector. So all you see in your second plot is a single point.
Generally, when you define a function expecting all scalar arguments (as all you functions do) and you want to call it with a vector as an argument, you should apply vectorization.
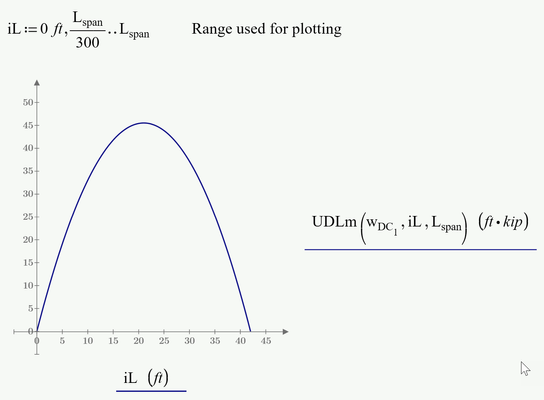
But I see no reason for the vector i-L anyway. You just use it for plotting and you get a rather rough, inexact plot using just 11 points for the parabola.
Why not define a more dense range and use it for the plot?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just for my own knowledge...why was the one function working okay without vectorization and the others weren't?
Pass a vector x into the above equation and the L/2-x is a scalar minus a vector that gets a vector, then a scalar times a vector that also gets a vector.
Pass a vector x into the above equation and you eventually get a vector by vector product. Matrix multiplication is not defined for two column vectors but a dot scalar product is so you get one value.
Cheers