Film Model: Sbval with multiple ODEs

[KHecht]

I am trying to solve a film model for diffusion and reaction of two species (liquid film of a gas/liquid reaction). The problem I would like to solve is described in sbval_Film_Model.xmcd (attached). At the interface (x=0) CA has a known value; CB is unknown, but dCB/dx=0. At the end of the film (x=dL), CA and CB are in a sense known, but depend on dCi/dX, i.e. the amount passing through the film.

I can't assume that CA(x=dL)=0.

I'd like to somehow solve this problem using sbval to estimate CB at x=0 and a standard ODE solver to obtain the concentration profiles in the film. Eventually I would like to solve the film profiles at different points along a reactor length, meaning I need something that can be implmented in programming and doesn't use a given block. Does any one know how to setup sbval when there are two variables (CA and CB) and not just one?

[Fred_Kohlhepp]

You might try attacking this problem using finite differences rather than SBVAL and the ODE solvers.

The first file solves a boundary value problem using finite differences. Basically a vector of solution values is guessed at, the differential equation is expressed using finite difference expressions in vector positions and the boundary values and the finite difference function are used in a solve block to find the values of the solution.

The second file develops the expression for different derivative replacement functions (forward difference, central difference, etc.)

The advantage of this method is that you can constrain the boundary (or a derivative of the function at the boundary) rather than an initial condition set (all of the ODE solvers are initial condition solvers, you need SBVAL to "guess" at the correct initial condition to arrive at the opposite boundary correct values.

I've looked at your problem, I can't develiop the equations from what I can see.

Good luck.

[KHecht]

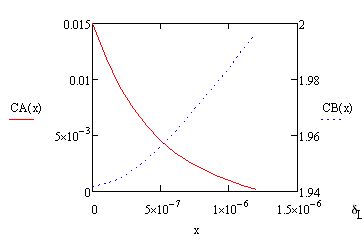
A finite difference solution would be very welcome. I tried to implement such a solution in the attached file film_model.xmcd. It's not as elegant as your proposed solution; in the red box I have to set the lowest guess value of CB (on a scale from 0 to 1) that still gives CB=1 at x=dL. I still have several problems:

1 - Boundary Condition: dCB/dx=0 @ x=0

Unfortunately, I don't know how to implement the boundary condition dCB/dx @ x=0 using this strategy. I could do this at the very first point, but at the rest of the points I would use k*CA*CB*x^2, so it wouldn't make any difference.

In another question (film_model_simplified.xmcd) I posted a solution using a solve block and odesolve but simple numbers for CA and CB at dL. Using the discretized approach, my solution looks like the left graph shown in green. If I use odesolve (or Matlab), the solutions looks like the right graph shown in white.

2- Boundary Conditions of CA and CB @ x=dL

CA and CB at x=dL aren't actually known, but depend on initial values plus dCA/dx and dCB/dx at x=dL. I assume that both of these derivatives are actually 0 at x=dL, but my professor wants me to make a model that is generally applicable and doesn't contain any assumptions. If the first point was properly addressed, this point would be rather easy to address.

3- Elements

My solution depends on the number of elements I use. Drastically. It doesn't seem to level out with an increasing number of elements.

[KHecht]

[Fred_Kohlhepp]

I can't get your non-dimensional problem to work--I'm not sure you're scaling it correctly, and I'm positive that I'm not.

But finite difference schemes will allow units, so I set up the problem using the basic uniit values and expressions. That works, more or less. Ssadly, this problem needs to be scaled to get an accurate solution.

Attached is what I have so far; maybe you will see something of value.

[Fred_Kohlhepp · Accepted solution]

Better scaling!

Need a boundary condition.

[KHecht]

Dear Fred,

your solution works brilliantly, and I've been using it to calculate single points. The next step is that I need to run this film calculation along the length of the reactor for N segments, i.e. as a subroutine where I can change the inputs each time. Do you have any suggestions? As far as I know this isn't possible with solve blocks, and I can't think of how to combine your solution with the add-line programming available in Mathcad.

[Fred_Kohlhepp]

You can Define a function to change the inputs to a solve block. It's not clear to me what you would change for the next solution iteration.

[KHecht]

Here is the final model that I came up with using your strategy for a 2D model of a gas/liquid reactor where the film balances are solved in each reactor cell. The number of cells in the film and along the reactor are defined at the bottom of the first page. I use the number of cells shown, but if you reduce each of them by 10, you can get a solution pretty quickly.