Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Geometry challenge
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Geometry challenge
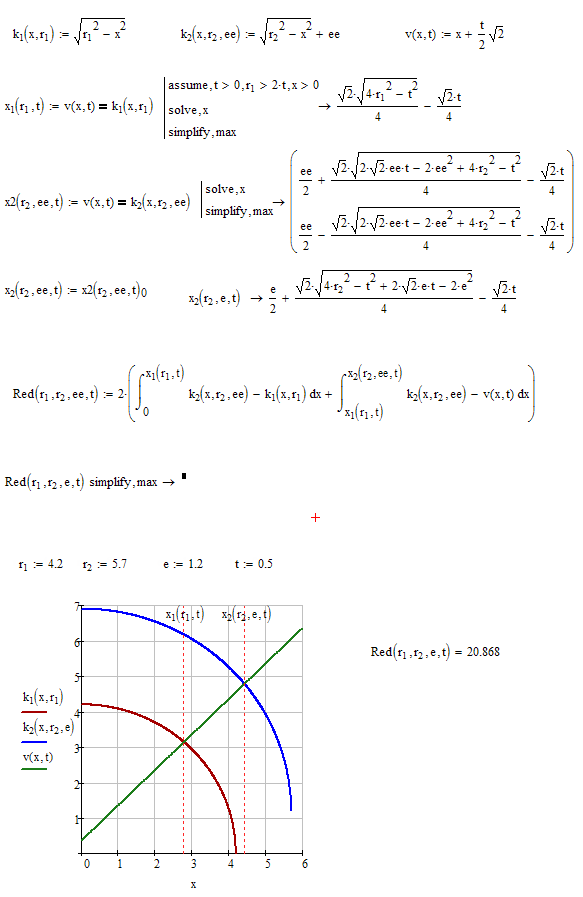
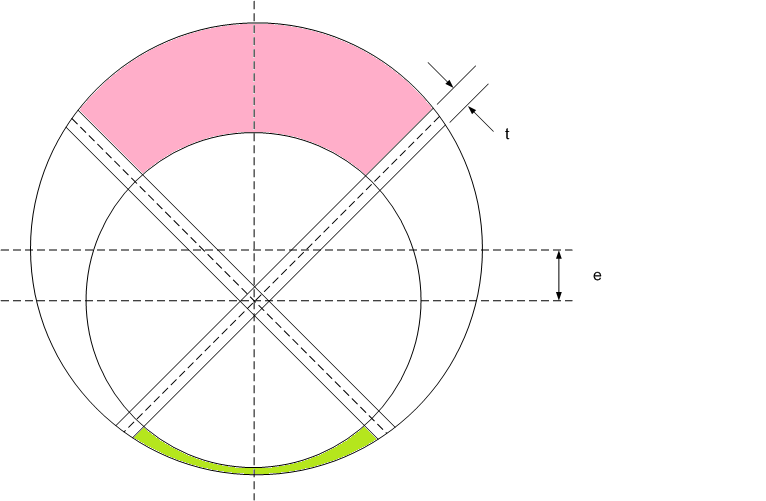
Nothing to do with Mathcad, but I know some of you enjoy a good challenge. And I'm stumped. Here's the situation: Two circles of different diameters, one vertically offset a distance e from the other. Vanes of thickness t are centered in the smaller circle. The vane are 90 degrees from each other. What are the top and bottom colored areas? I'll gladly take any hints on how you'd do it.
Thanks!
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You state that the two vanes are 90 deg from each other, but do not clarify orientation relative to the vertical offset of the circles. Please verify that the vanes are each 45 deg from vertical.
How accurate must the answer be? Assuming thickness t is small, is it sufficient to assume the area of a vane is equal to its length times thickness?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, the vanes are 45 from vertical (so we have symmetry). The answer needs to be quiet exact so I'm looking for a mathematically pure result. 1% error would be unacceptable. (It's a pump in case you're wondering.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Need an exercise in polar coordinates.
Attached solves top half.
Bottom half is exercise for next.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Fred,
The lower half, would changing "ee" to:

work?
Norm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about this?

B can be determined from e & t.
Solve for A:

The second solution is negative, so use the first solution.
With A, you should be able to solve your area by addition/subtraction of circular segments and triangles.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner. I knew I just wasn't looking at it simply enough. Bottom half solution is solved by simply entering a negative eccentricity (e). Matches my CAD answers exactly so I'm calling it solved.
I'll have to absorb everyone else's solutions also. Thanks everyone for the efforts.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi dferry,
although the problem is still solved, i calculated it with Prime 4.0.
A very good challenge and exercise for creating multiple Integrals.
And yes- to calculate the smaller Area there must be changed only "ey" to a negative sign.
I added an analytical solution for both Areas at the end of the Worksheet.
best regards, Volker