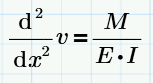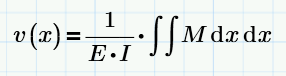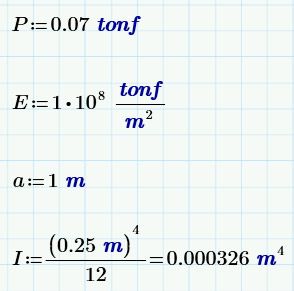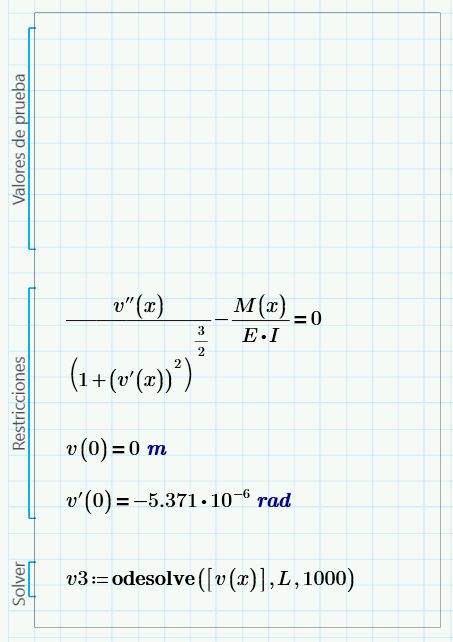Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help to solve the second-order nonlinear differential equation applied to the deflection of a beam
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Help to solve the second-order nonlinear differential equation applied to the deflection of a beam
Greetings dear colleagues of the forum, I am looking for help to solve the non-linear differential equation of second order corresponding to a beam:
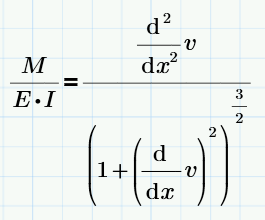
- M is a function that is written in terms of x. This function is variable, it depends on the loads applied to the beam.
- E and I are constant values. The first is the modulus of elasticity (E) and the second corresponds to the moment of inertia (I).
- v is the unknown that I want to obtain and is written in terms of x. Varies for each beam, same as M, depending on the configuration of applied loads.
I am interested in clearing the deflection "v" that occurs in the beam since I am verifying the results obtained with a structural analysis software called Ftool (https://www.ftool.com.br/Ftoo
In most books they only present exercises using the previous equation but in its reduced (simplified) version:
In this case the solution consists of integrating twice, obtaining:
Resolving several cases by hand and comparing with that obtained with the Ftool software there are differences in the results, product of using the simplified equation.
I would appreciate any help to solve this equation.
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is that your function names have an index.
Mathcad15 applies the prime symbols to the index (which usually looks silly and wrong anyway). This is a consequence of the fact that in this version ALL characters after the dot are seen as subscripts.
The converter is not clever enough to cope with that (it sure should) and leaves the prime symbols at the index which results in a strange Prime error. Prime will only accept the prime symbols to the function name as a whole and not at the index (which is correct behaviour).
So you have to manually transfer the prime symbols from the subscript up to the end of the function name and this editing is quite uncomfortable in Prime - especially when using a version like mine where the shortcut for the prime symbol simply does not work as stated.
Find the corrected version attached (Format P5)
BTW - you may consider using units!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
This is Mathcad 15. It shows the comparison of each one using the ODEsolve.
If 15 proves too hard I guess it can be converted to Prime
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
The conversion to Prime that is not so good so needs tidy up.
Cheers Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem is that your function names have an index.
Mathcad15 applies the prime symbols to the index (which usually looks silly and wrong anyway). This is a consequence of the fact that in this version ALL characters after the dot are seen as subscripts.
The converter is not clever enough to cope with that (it sure should) and leaves the prime symbols at the index which results in a strange Prime error. Prime will only accept the prime symbols to the function name as a whole and not at the index (which is correct behaviour).
So you have to manually transfer the prime symbols from the subscript up to the end of the function name and this editing is quite uncomfortable in Prime - especially when using a version like mine where the shortcut for the prime symbol simply does not work as stated.
Find the corrected version attached (Format P5)
BTW - you may consider using units!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Thanks Werner.
I wanted the numbers to be representative of real life. I have changed the inertia of the beam to 300 x 10^6 not 3 x 10^6. This represents a heavily loaded steel beam which deflects a little to much around 19 mm.
The difference in the more refined equation for M is only a fraction of percent and that is why the more complex equation is not bothered with in practical engineering. It is of academic interest only.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for your help Terry, it has been very useful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for your help Werner, it has been very useful. I already checked the calculated with the general equation vs the results of Ftool and they are OK. I work with Mathcad Prime 4:
I had not used Odesolve before, I see that it is numerically powerful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
With a little help of Mathcad 11/Maple:
Given a suitable definition of M(x) and boundary conditions to solve the two integration constants C0 and C1, you should be to calculate v(x).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your input, I will study your suggestion.
Although solving symbolically can be very long and complex for this equation. Mathcad Prime does not give me a solution for this case, I will try to see in Maple.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I gave you the full symbolic expression of v(x,...). You could type that into Prime and see for yourself what comes out in benchmarking. I wasn't able so far, because you did not provide the full Prime sheet and left it to guessing what exactly your system is: I wonder what the definitions of L and M(x) are that you used in comparing the Odesolve results with the results of that other tool.
Success!
Luc